BitCoins and Mining

Questions:

Contents

• Reflection part 1 Some Technical data

Purpose

Answer question 1 - What is a BitCoin

Answer question 2 - What is Blockchain

Answer question 3 - What is Mining

Mining is the process of creating new bitcoins. This process of mining is called a puzzle. When you solve the puzzle you get a reward and this reward are 50 bitcoins. This reward becomes less untill it is zero. Than mining stops.
The puzzle in fact is a mathematical calculation to find a number. The rules are relative simple. When you have found this number the next problem is the same with only one constraint: the number has to be smaller. The problem is: how smaller the number, how longer it takes to calculate this number.
The idea behind the calculation is to code a message. Each message consists of a sequence of letters. Inside a computer each message is a sequence of bits. For example a message like ABCD, written in bits looks like: 01000001 01000010 01000011 and 01000100.
In hexadecimal notation the message ABCD looks like: 41,42,43 en 44.
The message ABCD contains 23 zero's and 9 one's and consits of 4 bytes of each 8 bits
When you code a message you follow a strict recipe of operations.

• one type of operation can be exchange For example: exchange bit 12 with bit 25. That means bit 12 becomes what bit 25 was and bit 25 becomes what bit 12 was. Bit 12 can be any bit the same as bit 25.
  When you that the total number of zero's and one's stays the same.
  Two possible results are: 00000000 00000000 00000001 1111111 and 11111111 10000000 00000000 00000000.
  The first sequence represents the smallest possible number (of 4 bytes). This number starts with all zero's. The second sequence represents the highest possible number. This number with all ones.
  
• A different type of operation is a replace operation. There are two types of replace operations: replace a bit with a one or replace a bit with a zero. For example replace bit 12 with a one or replace bit 25 with a zero.
  The purpose of this operation is that the total number of zero's and one's will change.
  A more technical name for this operation is the exclusive or operation.

As explained above the whole idea is to code a message ABCD using a strict recipe of operations. This strict recipe can be a sequence of for example 30 exchange or replace operations. When you do that the final result will be a sequence of 32 bits ie a number. The whole idea is that some one else who also starts with the message ABCD and follows the same sequence of 30 operations will get the same result. In fact any body can check if what you have calculated is correct. That is the type of security that is build in the Blockchain technology.
In the above the operations are explained at bit level i.e. only individual bits are involved. In reality the operations are more done at byte (level) level i.e. between different bytes or at register level (groups of bytes). This makes everything code process slightly more complex, but the idea stays the same: everyone does the same.

When you start message is ABCD that is not the whole message you use. In reality the message you are going to code is ABCD0001. That means a combination of the Message ABCD and number 0001 (order number). The result (using the recipe of 30 operations) is value #1. Next you increase the order number with 1 i.e becomes 0002, you code again and you get value #2. Next you use 0003 and you get value #3 etc etc.
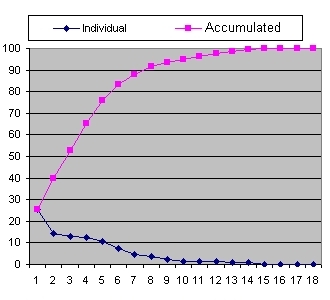
The whole idea is that each of these values starts with a certain number of zero bits.

• At position 1 (bit 1) of all the values 50% will have a one and 50% will have a zero.
  
• Out of these last values at position bit 2: 50% will have a 1 and 50% will have a zero. That means 25% will start with two zero bits
  
• Out of these last values at position bit 3: 50% will have a 1 and 50% will have a zero. That means 12.5% (or each 8 operations) will start with three zero bits
  In 6.25% (or each 16 calculations) you get 4 zero bits and in 3.125% (or each 32 calculations) you get 5 zero bits.

What this explains that in general it takes more and more calculations to calculate a smaller number. The number of calculations increases with a power of 2. The power is the number of zero bits.

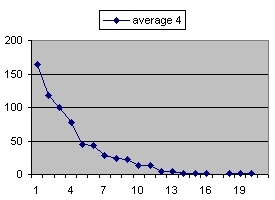
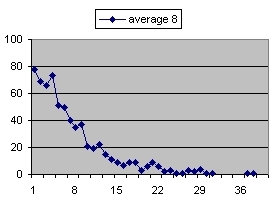
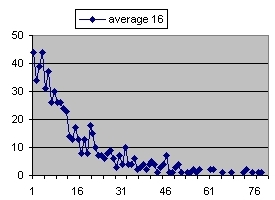
The following table shows the result of a simulation based on 664 calculations.

bits hex limit # calc expect deviation 1 01 4 0,5 2,05 1,02 1,38 2 001 2 0,25 3,94 0,98 3,19 3 0001 1 0,125 7,28 0,91 6,39 4 00001 08 0,0625 15,73 0,98 15,59 5 000001 04 0,03125 31,84 0.99 32,27 6 0000001 02 0,015625 65,80 1,03 68,19 7 00000001 01 0,0078125 138,04 1,08 134,06 8 000000001 008 0,00390625 275,20 1,07 272,60 9 0000000001 004 0,001953125 544,09 1,06 530,72 10 00000000001 002 0,000976563 1034,60 1,01 952,78 11 000000000001 001 0,000488281 2032,00 0,99 1902,55 12 0000000000001 0008 0,000244141 4025,24 0,98 3792,76

In the above text it is explained that a high number always starts with a 1 bit. A higher number starts with two 1 bits and an even higher number with three one bits i.e. 111
For the low number the same logic applies. A low number always starts with a zero bit. A lower number with two zero bits and an even lower number with three zero bits i.e. 000
You can also express each number as a fraction between 0 and 1. That means any number that starts with a one has a value equal or higher than 0.5. Any value that starts with one zero has a value lower than 0.5 Any value that starts with two zero's has a value lower than 0.25 Any number with starts with three zero's has a value lower than 0.125 etc

Each line shows the results of the simulations how many calculations (on average) are needed to calculate a value that is smaller than a certain limit. This limit is shown in column 3 and the # of calculations in column 4

• The first line shows that on average 2,05 calculations are needed to get a value that is lower than 0.5
  The theoretical value is 2. When you divide 2,05 by 2 you get 1.03 This number in column 6 indicates that the number of calculations performed is slightly more as predicted.
• The second line shows that on average 3,95 calculations to get a value that is lower than 0,25. The theoretical value is 4
  
• The fourth line shows that on average 15,78 calculations to get a value that is lower than 0,0625. The theoretical value is 16 Line 4 also shows that the limit value in hexadecimal notation is "08". This is the number in column 4.
  What this means that on average to get a value that starts with a zero in hexadecimal notation you need 16 calculations.
• Line 8 shows that on average 274,25 calculations to get a value that is lower than 0,0039. The theoretical value is 256 or 2^8.Line 8 also shows that the limit value in hexadecimal notation is "008".
  What this means that on average to get a value that starts with two zero's in hexadecimal notation you need 256 calculations.

The real lesson is that if you want a value smaller than "00000000" or 8 zero's in hexadecimal notation you need 2^32 calculations or 429497296 calculations. To calculate a value starting with 44 bits you need 2^44 or 17592186044416 calculations

Answer question 4 - How does a bitcoin compare with an Euro

To get a better insight about the difference between conventional currency versus crypto currency select the following two links:

1. A World with one currency. 2. A World with two currencies

• The first link discusses the situation of an isolated region where there exists only one currency.
• The second link discusses the situation of a two regions, each with its own currency and with trade between the two regions.

The emphasis is on bitcoins.

Answer question 5 - What is a Wallet

Answer question 6 - In the Bitcoin environment is there a Bank ?

In principle any Bank can have a Bitcoin account (also called a wallet). That means banks can trade in bitcoins. That means banks can sell and receive bitcoins between other banks and individuals. Banks in bitcoins can also sell and receive euro's using an exchange rate.

• Banks can serve as a savings institution in bitcoins. That means any private party can send bitcoins to Bank. When you do that the bank will open an bitcoin account in your name, which contains this initial amount as a credit. The total amount of bitcoins that the bank owns increases.
• Banks can also serve as a credit institution in bitcoins. When you do that the bank will open a bitcoin account in your name which contains an this initial amount. Using that account you can pay your bills in bitcoins. When the bank does that its total number of bitcoins owned by the bank will decrease.

For more detail see the next question.

---

Answer question 7 - In the Bitcoin environment can a bank create money?

The underlying question is: if Banks in bitcoins can do the same as a regular bank
What a regular bank can do is that it can create money. Creating money means that when one individual deposits money in a bank the bank can use that as a reserve. Using that reserve as a security the bank can lend money to any other third party. In fact a bank can lend more than what is has in reserve.
The tricky part is that in this case the lending party does not physical owns the coins. This is much more a paper excercise. It is a deal made on trust between two parties.

• First a trust from the customer that the money saved in the Bank is save
• Secondly a trust between the customer and the bank that the customer is going to pay back its debt.
• Third a trust from the bank that the customer only wants a small percentage of his money in cash.

1. Suppose you have a bank X who has an empty account of bitcoins.
2. Suppose you have customer A who has a wallet which contains a certain amount A of bitcoins.
3. Next customer opens a bitcoin account with bank X and transfers all his bitcoins to Bank X. Now Customer A has zero bitcoins in his Wallet and bank X has A bitcoins.
4. Suppose you have customer B who wants to lend B bitcoins. In that case bank X opens a bitbank account for customer B, which contains B bitcoins. The bank still has A bitcoins.
   As a safety measure the bank will ask customer B to give something as security i.e. cash in Euro's or a house.
5. Suppose customer A wants to buy or sell something from customer B. This is trading between different accounts of bank X and has no effect on the number of bitcoins.
6. Suppose customer B wants to buy something from customer C (a house) who has no bank account. In that case the bank X has to actual transfer bitcoins to customer C. In that case the number of bitcoins owned by bank X will deminish.

What a bank wants is customers similar as customer A. This are the customers who have a job. Are paid in Euro's. With this money they buy bitcoins and transfer them to their bitcoins accounts of bank X. As long as these customers don't spend more bitcoins as they own there is no problem.
Customers like B can become a problem for a bank because they are have a debt to the bank. This total amount can be larger as the number of bitcoins owned. This is no problem as long as all these customers don't spend their bitcoins. This becomes a problem if they are going to spend more bitcoins that the number of bitcoins owned by the bank . In that situation the bank has than to buy bitcoins (on the free market) against Euro's. The price of the bitcoins will increase.
Customers like B have to pay interest to the bank. In order to do that they have to buy bitcoins on the free market.

Reflection part 1 - Litterature

• A very could source to read about bitcoins is Wikipedia: https://en.wikipedia.org/wiki/Bitcoin
• To investigate the first blockchain select: https://blockchain.info/block/000000000019d6689c085ae165831e934ff763ae46a2a6c172b3f1b60a8ce26f
  The url shows:
  • The hash code of block 1. The first 20 characters are: "000000000019d6689c08". The first 10 are all zero's.
    The hash code is written in what is called hexadecimal notation. In hexadecimal notation each character stands for 4 bits, that means that the hash code starts with 40 zero bits (If you count carefull this are 43 zero bits).
  • The hash code of the previous block. In this special case there is no previous block.
  • The hash code of the next block.
• To investigate more blockchains select: https://blockchain.info/nl/blocks The url shows all blocks mined on the present day. The number is roughly 150.
  What the url shows are the mining companies involved.
  The following table is an overview based on 339 blocks. Each column shows the results of what are called mining rigs. The first row shows the name of the company, the second row shows the number of blocks mined and the third row the percentage.

  BTC.com ViaBTC BTC.TOP SlushPool AntPool Unknown F2 POOL BTCC Pool BitClub network Bitcoin.com 72 57 44 43 40 23 16 12 9 7 21.24 16,81 12.98 12.68 11.80 6.78 4.72 3.54 2.65 2.06

  The following companies have a market share of less than 2%:
  
  58COIN (6), BW.Com(5), BitFury(2), GBMiners(1), KanoPool(1) and P2Pool(1)
  1. The largest mining companies is BTC.com with roughly 21% of the market. For more detail select: https://pool.btc.com/
  2. The second largest is ViaBTC. For more detail select: https://pool.btc.com/
     To get some technical information select this link: https://viabtc.com/contract/s9/
  3. The two next largest companies are: https://pool.btc.com/ and https://slushpool.com/home/
  4. What makes this so interesting is that as far as I understand this all companies are performing the same operations.

The graphic on the right side shows the mining results. The blue line at the bottom shows the individual results of 18 companies of roughly 2000 block chains. The magenta line shows the Accumulated results. What the data shows is that 5 companies control 76% of the market. See also: https://en.wikipedia.org/wiki/Bitcoin#Decentralization . In that document the value 75% is given for 6 companies as of 2013. This implies a certain concentration is taken place.

Feedback

Back to my home page Contents of This Document