 Figure 8
Figure 8
|
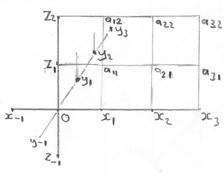
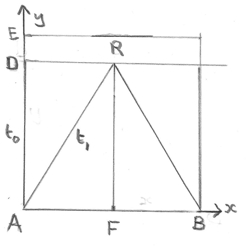
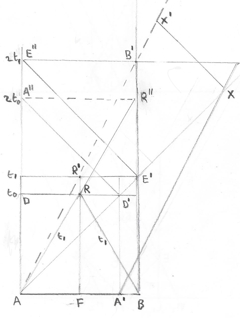
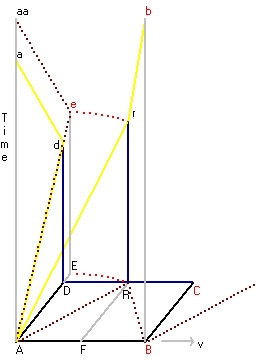
Figure 8 on the left represents the x,y,t spacetime frame of the experiment with two parallel mirrors.
- The mirror in front contains the points aa, a, A, F, B and b.
- The mirror in the back contains the points d, D, R, C and r.
4 world lines are displayed.
- The yellow line A-d-a represents the lightpath of a photon which travels from A to D, is reflected back, against the mirror, to A.
The same for a photon which travels from F to R and back to R.
The line represents the world line of rocket at rest.
- The line A-r (in the plane A,R,r) and the line r-b (in the plane R,B,b,r) together are the worldline of the lightpath of the photon which travels from A to R to B.
The line represents the world line of a moving rocket.
- The line A-e-aa represents the lightpath of a photon which travels from A to E (reflected) and back to A.
Because the length A-E and A-R are the same, the length of this line also represents the length of the light path going from A to R to B.
- the line A-b (not shown) in the plane A,B,b represents the worldline of the moving rocket in the laboratory frame.
|