Quantum Unspeakable

Introduction

This document contains comments about the book "Quantum Unspeakables" by R.A. Bertlmann and Anton Zeilinger
For a partly copy of the book see: Quantum Unspeakable
The parts copied are in italics
The main reason of the comments is to challenge the importance of the Bell inequality theorem. See also Bell test loopholes and Bell correlations and equal time measurements

Comments

At page 10 we read:
Clearly his famous quantum papers were very close to sugggesting actual performable experiments
Does this mean that John Bell never performed any actual experiments?

At page 23 we read: (d'Espagnat)

Well John Bell was good at elaborating computing methods at finding out "rules" leading to correct predictions and, more generally, at exerting the normal activity of a theoretical physicist.
If you can invent "rules", you are brillant, on the other hand performing actual experiments, in order to demonstrate those "rules", is the most important.

The sentence is interesting because it tells us that Bell is more a mathematician than a physicist.

At page 23 (Last line) we read: (d'Espagnat)

When we take a look at the life long disagreement betwee Einstein and Bohr, we cannot but observe that the reason why they could never satisfactorily resolve it is that it was most deeply philosophical
IMO strange. This requires a longer explanation. Specific it would be nice to know, where they agree.

At page 24 (line 6) we read:

"Is a realistic, local theory of the universe acceptable?" Thanks to John Bell, we know that the answer is no.
IMO this question is not clear and as such you cannot answer it.

At page 25 (line 30) we read:

Feynman bluntly states that "nobody can explain more than we have explained... We have no idea whatsoever of a more basic mechanism from which the foregoing results (the interference fringes) could be deduced"
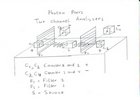
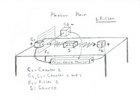
Interesting, but be carefull this is not about photon pairs but about preposterous statements.

At page 72 (line 10) we read:

To be sure, there remained alive a minority of the theory's founders (notably Einstein, Schrodinger and de Broglie) who were still critical of the theory foundations.

A little further we read:
On many occasions, I was personally told as a student that these men had become senile and that clearly their opinions could no longer be trusted in this regard
IMO the opposite is more closely to the truth.

At page 73 we read:

Perhaps for this reason, not much ..on Bell's Theorem was formally published until it much of it was later collected into his book, Speakable and unspeakable in quantum mechanics
At page xxvi of that last book we read:
Beginning in the 1970s, physicists invented methods to manipulate and observe single elementary objects - such as single photon, electron or ion.
That being the case, how can you have any fruitfull discussion before that day ? This explains why they were all talking about "thaught experiments" and not about actual experiments.

At page 74 we read:

Originally, EPR had discussed entanglement in terms of the continuous variables, momentum and position. In this book, Bohm reformulates the configuration in terms of entangled discrete-state systems i.e. in terms of the spin component correlations of two spin-1/2 atoms in a spin-singlet entangled state.
IMO it is not make sense to discuss entanglement based on momentum and position, which are calculated variables based on measured values, of one indivisible object. From historical context this sentence is interesting.

Page 120

At page 120 we read:
I give a more detailed description of .... with a dramatically improved source of pairs of entangled photons.
The question here is what are photon pairs.
The answer is a photon pair are two photons which are created by one event i.e. simultaneous

A much more important question is: How do you demonstrate that you are using a pair of photons.
The answer is by using a Coincidence Monitor or CM. With a CM you can investigate the individual moments that the photons are counted and decide if they are simultaneous or not
The following experiment describes the most simple configuration of a Coincidence Monitor 

Counter 1--------<----------Source----------->--------Counter 2
   ^                                                     ^
   |                                                     |
   |------------------Coincidence Monitor----------------|
                                              
          Basic Configuration - Experiment 1
For a 3D sketch see: photon pair
What we have is a source (which transmits photon pairs), two counters and a Coincidence Monitor.
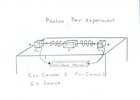
The experiment takes place for a fixed duration of time t1.
  • We have a source which tranmits photon pairs. One goes to the left one goes towards the right.
  • Counter 1 is used to count the left photons. The total count is tn1.
  • Counter 2 is used to count the left photons. The total count is tn2.
  • A Coincidence Monitor to investigate the individual events. As such we get:
    1. n12: number of simultaneous events of counter 1 and 2
    2. n1: number of single events detected with counter 1
    3. n2: number of single events detected with counter 2 
Counter 1: x x  x x  x x x  x  x x   x  x   x x    x  x x   x tn1 = 18
Counter 2: x x  x    x x    x  x x   x  x x x x  x x  x x   x tn2 = 18
In the above example we get: n12 = 16, n1 = 2 and n2 = 2. That means 16 photon pairs are detected and 4 not.

Page 121

At Page 121 we read:
We perform a lineair polarization measurements of two photons, with analysers 1 and 2. Analyser 1, in orientation a, is followed by two detectors, giving results + or -, corresponding to a lineair polarization found parallel or perpendicular to a. Analyser 2, in orientation b, acts similary
What we are discussing is an experiment with photon pairs and a Two Channel Analyzer.
                     Experiment  3

             0 degrees                        0 degrees
Counter 1<----Filter1<---------Source--------->Filter2---->Counter 2
   ^ (+)         |                                |          ^ (+)
   |             V                                V          |
   |         Counter 3 (-)                   Counter 4 (-)   |
   |             ^                                ^          | 
   |             |                                |          |
    --------------------Coincidence Monitor------------------
For a 3D sketch see: photon pair
What we have is a source which transmits photon pairs in two directions.
At each side we have one filter and two counters i.e. one counter which counts when the photon goes through and one counter which counts when the photon is absorbed.
Suppose the source emits two photons which have the same polarization angle alpha and suppose the two filters each have the same polarization angle alpha
If this is the case either both Counter1 and Counter2 will increment and not Counter3 and Counter 4 or both Counter3 and Counter4 will increment and not Counter1 and Counter2

Page 122

At page 122 we read:
Quantum mechanics predicts the following:
P+(a)=P-(a)=1/2
P+(b)=P-(b)=1/2
This are the equations (9.2)
These results are in agreement with the remark that we cannot assign any polarization to each photon, so that each individual polarization measurement gives a random result.
  1. P+(a) means is to find a photon in Analyser 1 with the direction a, parallel to a.
  2. P-(a) means is to find a photon in Analyser 1 with the direction a, perpendicular to a.
  3. P+(b) means is to find a photon in Analyser 2 with the direction b, parallel to b.
  4. P-(b) means is to find a photon in Analyser 2 with the direction b, perpendicular to b.
Logical thinking this result seems correct, because a photon is either detected at analyser 1 by one or the other detector.
But is this also true in reality. To find out we remove the second filter and we count for a certain fixed duration the number of counts at each counter C1, C2 and C3
                       Experiment 2

             0 degrees
Counter 1<----Filter1<---------Source--------------------->Counter 2
   ^ (+)         |                                           ^ (+)
   |             V                                           |
   |         Counter 3 (-)                                   |
   |             ^                                           | 
   |             |                                           |
    --------------------Coincidence Monitor------------------
For a 3D sketch see: photon pair
  1. tn1 the total number of counts of c1.
  2. tn2 the total number of counts of c2.
  3. tn3 the total number of counts of c3.
The most logical situation is that tn1 = 500. tn2 = 1000 and tn3 = 500
Using simple arthimatic we get P+(a) = tn1/tn2 = 1/2 and P-(a) = tn3/tn2 = 1/2

Using the Coincidence Monitor we get the following additional counts:

  1. n123: This is the number of coincidence counts of c1,c2 and c3.
  2. n12: This is the number of coincidence counts of c1 and c2.
  3. n23: This is the number of coincidence counts of c2 and c3.
  4. n13: This is the number of coincidence counts of c1 and c3.
  5. n1: This is the number of single events detected at Counter 1
  6. n2: This is the number of single events detected at Counter 2
  7. n3: This is the number of single events detected at Counter 3
Again the most logical situation is that n123= 0. n12 = tn1, n32 = tn3 and tn2 = n12 + n32. But that is not necessary. It is easy possible that n12 is smaller than tn1 and that n32 is smaller than tn3.

The results of the experiment could be something like this: 

Counter 1: x    x x    x       x     x        x    x  x       tn1 =  9
Counter 3:   x       x   x  x    x      x   x      x    x   x tn3 = 10
Counter 2: x x  x    x x    x  x x   x  x x x x  x x  x x   x tn2 = 18
In the above example we get: n123 = 1, n12=7, n32=8, n13=0, n1=1, n2=2, and n3=1
The total number of events tn = n123+n12+n32+n13+n1+n2+n3 = 20.
The final results are:
P+(a) = n12/tn = 7/20 = 35%
P-(a) = n32/tn = 8/20 = 40%

Paragraph 9.2.2

At page 122 we read:
Consider first the particular situation where polarizers are parallel. The quantum mechanical predictions for the joint detection probabilities are:
P++(a,a) = P--(a,a) = 1/2
P+-(a,a) = P-+(a,a) = 0
This are the equations (9.4)
According to this result, and taking into account (9.2), we conclude than when photon 1 is found in the + channel of polarizer 1, photon 2 is found with certainty in the + channel of polarizer 2 (and the same for the - channels)
The question is: is this true?
The only way is to test and to perform the above experiment described at page 122.
In that case we have 4 counters and the result of the experiment is four total counts tn1,tn2,tn3 and tn4.
With the Coincidence Monitor we get the following simultaneous counts:
n1234, n123, n124, n134, n234, n12, n13, n14, n23, n24, n34, n1,n2,n3 and n4
Counter 1: x    x x    x       x     x        x    x  x       tn1 = 9
Counter 3:   x       x   x  x    x      x   x      x    x   x tn3 = 10
Counter 2: x    x      x       x          x x x    x  x       tn2 = 9
Counter 4:   x       x      x    x   x  x        x x    x   x tn4 = 10
In the above example we get: n1234 = 1, n12=6, n34=7, n14=1, n23=1, n1=1, n2=1, n3=1 and n4=1
The total number of events tn = n1234+n12+n34+n14+n23+n1+n2+n3+n4 = 20.
The final results are:
P++(a,a) = n12/tn = 6/20 = 30%
P--(a,a) = n34/tn = 7/20 = 35%
P+-(a,a) = n14/tn = 1/20 = 5%
P-+(a,a) = n32/tn = 1/20 = 5%
In the above test the two polarizers are paralel to each other. We can also perform the same test changing the direction of the second analyser to perpendicular
The results of the experiment could than be something like this: 
Counter 1: x    x x    x       x     x        x    x  x       tn1 = 9
Counter 3:   x       x   x  x    x      x   x      x    x   x tn3 = 10
Counter 2:   x       x      x    x   x  x        x x    x   x tn2 = 10
Counter 4: x    x      x       x          x x x    x  x       tn4 = 9
In the above example we get: n1234 = 1, n12=1, n34=1, n14=6, n23=7, n1=1, n2=1, n3=1 and n4=1
The total number of events tn = n1234+n12+n34+n14+n23+n1+n2+n3+n4 = 20.
The final results are:
P++(a,b) = n12/tn = 1/20 = 5%
P--(a,b) = n34/tn = 1/20 = 5%
P+-(a,b) = n14/tn = 6/20 = 30%
P-+(a,b) = n32/tn = 7/20 = 35%

We can also perform the same test changing the direction of the second analyser to 45 degrees
The results of the experiment could than be something like this: 

Counter 1: x    x x    x       x     x        x    x  x       tn1 = 9
Counter 3:   x       x   x  x    x      x   x      x    x   x tn3 = 10
Counter 2: x x              x  x x   x        x  x x    x     tn2 = 10
Counter 4:      x    x x                x x x      x  x     x tn4 = 9
In the above example we get: n1234 = 1, n12=4, n34=4, n14=3, n23=4, n1=1, n2=1, n3=1 and n4=1
The total number of events tn = n1234+n12+n34+n14+n23+n1+n2+n3+n4 = 20.
The final results are:
P++(a,b) = n12/tn = 4/20 = 20%
P--(a,b) = n34/tn = 4/20 = 20%
P+-(a,b) = n14/tn = 3/20 = 15%
P-+(a,b) = n32/tn = 4/20 = 20%
This result is identical as when the angle between the two polarization planes is random i.e. there is no entanglement.

Page 132

At page 132 we read:
Note, however that Einstein did not know Bell's theorem, and he could logically think that his world view was compatible with the algebraic predictions of quantum mechanics. It is impossible to know what would have been his reaction to the contradiction revealed by Bell's theorem.
IMO Einstein's point of view would be that Bell's theorem is not a tool to decide who is right: Einstein or Bohr.

Reflection Part 1.

The subject of the book is about photon pairs.
  1. What are photon pairs?
    Answer: Photon pairs are at least two photons generatated simultaneous by the same event.
  2. How do you prove that two photons are a photon pair ?
    Answer: You do that by performing experiments in slow motion, such that when you observe the photons (i.e. detecting them by means of a counter) you can establish that the two photons have the same origin.
    In reality you should try to monitor 100 events. Those 100 events form a sequence of events, like the rings of tree, with different distances between each. You get 2 of those sequences. Comparing those two should reveal a close to 100% match. If not then you have no pairs.
  3. What type of photon pairs are there?
    Answer: Correlated and non correlated.
  4. How do you find out if you have correlated versus non correlated photon pairs?
    Answer: By placing a filter in between the source and the counter with the same angle in both the left and the right direction.
    You again monitor the 100 events. In the + direction you will only get 50 of those events (in both directions).
    • You have correlated pairs when the match between the 50 events of left squence with the right sequence is almost 100% or 0%.
    • You have non Correlated pairs when this match between the two sequences of events is close to 50%. That means in one direction you get 25 simulataneous and 25 non simulataneous events.
  5. Is there a difference between one channel analyzer versus a two channel analyzer.
    Answer:
    • In a one channel analyzer you only get a count when the photon goes through the filter. When the photon is absorbed you see nothing.
    • In a two channel analyzer you get a count when the photon goes through (this is a + direction) or when the photon is absorbed (this is the - direction). Different counters are used in the + and - direction.
    In theory the one channel analyser and the counter in the + direction of a two channel analyzer should give the same result. In practice this should be tested if this is true.
  6. What is the physical explanation for the non correlated versus a correlated photon pair. Answer: Both are created simultaneous at the source.
    A photon can be visualized as vibrating in one particular plane. Also called polarisation plane or the plane of the E vector.
    • For a random photon pair the angle between those plane can have any value.
    • For a correlated photon pair (Also called entangled) the angle is either:
      0 degrees. This is the case when the correlation of simultaneous events is 100%
      90 degrees. This is the case when the correlation is 0 %

IMO all of the above is important to improve our understanding

Reflection Part 2.

To what extend is the claim that "quantum mechanics makes predictions" correct ?
IMO the above experiments do not prove anything related to quantum mechanics.
Quantum mechanics does not predict the outcome of those experiments

The only thing what those experiments demonstrate, is that there are apparently three different types of processes which produce a photon pair
Experiments with polarisation glasses demonstrate that each photon can be visualised as moving in a particular polarization plane.
When you have a photon pair each of those photons "moves"" in its own polarization plane
As such we have processes:

The question to ask is: What are the characteristics of each of those processes.

Feedback

None
If you want to give a comment you can use the following form Comment form
Created: 15 May 2009

Go Back to Book and Article Review
Back to my home page Contents of This Document