Introduction and Purpose

• Spreadsheet "x=x" is described at this link: Findprim shor.xls.htm#par2. 2. Spreadsheet layout: "Get Pr1". Button "Get Prime 1"
• Spreadsheet "x=2" simulates the example 4 which uses x=2.
• Spreadsheet "T?" also simulates example 4 without what is identified as the GCD concept.
• Original I hoped that spreadsheet "T?" was capable to handle all possible combinations of prime numbers. But alas, that was not true.
  
  Spreadsheet "T1" explains what the error is, and how to solve this problem.
• Spreadsheet "T234" demonstrates in more detail the problem, and that the solution has a high chance to work for all cases.

For a copy of the Excel program in zip format select: FINDPRIM_array_x.zip

Contents

• 1. Spreadsheet layout: "x=x"
• 1.1 General Description Spreadsheet: "x=x"
• 1.2 Operation of spreadsheet "x=x"
• 1.3 Discussion
• 2. Spreadsheet layout: "x=2"
• 2. Operation spreadsheet: "x=2"
• 2.2 Discussion
• 3. Spreadsheet layout: "Type = ?"
• 3.1 Operation spreadsheet: "T?"
• 3.2 Discussion
• 4. Spreadsheet layout: "Type = 1"
• 4.1 Operation spreadsheet: "T1"
• 4.2 Discussion
• 5. Spreadsheet layout: "Type = 234"
• 5.1 Operation spreadsheet: "T234"
• 5.2 Discussion

Reflection

• Reflection 1 - - Phase 2
• Reflection 2 -
• Reflection 3 -

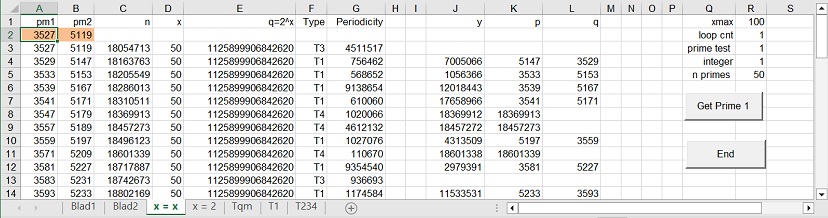
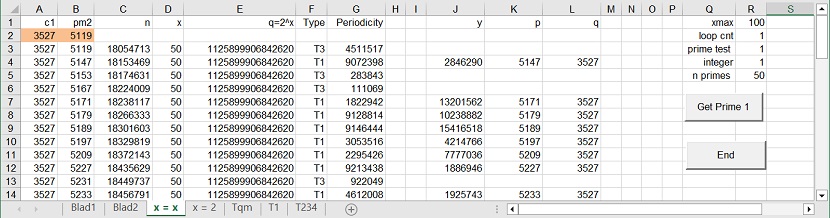
1. Spreadsheet layout: "x=x"

Figure 1A: pm1 = pm1 Figure 1B: pm1 = c1

1.1 General Description of Spreadsheet: "x=x"

The program is a simulation of Shor's Algorithm as described in this document: 2. Spreadsheet layout: "Get Pr1". Button "Get Prime 1" which is part of the Excel program "Findprim shor.xls".
The layout is shown as Figure 1A and as Figure 1B.
Both Figures show the following columns:

• Column A: pm1 or primary number 1.
  
• Column B: pm2 or primary number 2.
  
• Column C: n. This is product of pm1 and pm2. n is the input of the algorithm.
  
• Column D: x. x is calculated as a function of n. For more details see above mentioned documentation.
  
• Column E: q. q = 2^x
  
• Column F: Type. There are 4 types possible: T1, T2, T3 and T4. T1 means no error. T2, T3 and T4 indicate an error.
• Column G: Periodicity
• Column J: Y. This is an intermediate result.
• Column K and L: P and Q. This are the calculated prime numbers.

There are 4 more parameters which control the execution of the program.

• cell(1,A). This cell contains the text pm1. This text can be changed to c1. c1 indicates that the prime number is a constant. In figure 1A cell(1,A) shows the text pm1 and in Figure 1B the text c1.
• cell(2,A) and cell(2,B). These cells contain the initial values of the two prime numbers used.
• cell(1,R). This cell contains xmax and is the maximum value of x, calculated in column 4.
• cell(5,R). This cell contains n primes which is the number prime number products factorized. Each of the prime numbers factorized occupies one row.

1.2 Operation of Spreadsheet "x=x"

1. In order to start the program, select the Get Prime 1 Command
2. Input for the program are two (prime) numbers: pm1 and pm2. Multiplication of those two (prime) numbers gives a number n in column 3, which is factorized using Shor's Algorithm. Those two numbers should be entered in the cells (2,A) and (2,B).
3. The number of prime number products factorized is controlled by the parameter n primes. The results are stored in one row.
4. At the beginning of each simulation n is calculated as a product of pm1 and pm2. That means in reality first pm1 and pm2 are calculated, which are the next higher prime numbers. pm2 should be higher as pm1.
5. The final result is stored in the columns P and Q.

1.3 Discussion

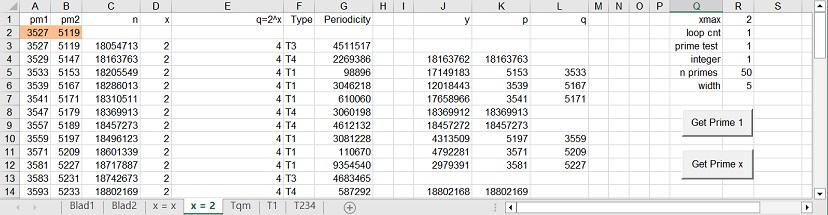
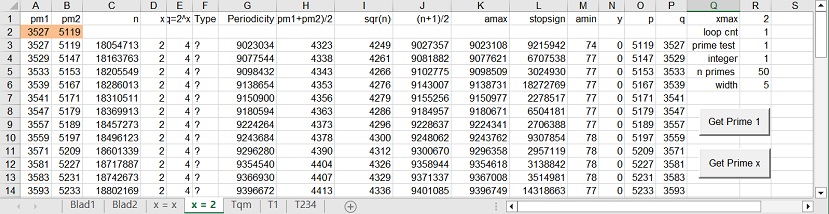
2. Spreadsheet layout: "x=2"

Figure 2A: Button = Get Prime 1 Figure 2B: Button = Get Prime x

2.1 Operation spreadsheet: "x=2"

Sheet "x=2" contains two buttons: "Get Prime 1" and "Get Prime X"

• "Get Prime 1" follows the functionality of 2. Spreadsheet layout: "Get Pr1". Button "Get Prime 1". The same as Sheet "x=x". The main difference that the parameter "xmax" = 2.
• "Get Prime x" follows the functionality of Shors Algorithm Question 11 Specific Example 4. This Example uses x=2. This functionality is also called: Calculating Periodicity in 5 easy steps.
  This same functionality is also described in: nature 12 January 2023 Are-quantum-computers-about-to-break-online-privacy.htm#ref2 #ref2 indicates: Reflection 2 - Factoring the product of two primes
  

2.2 Discussion

• What can easily be observed is that the performance of "Get Prime x" is much faster than "Get Prime 1".
• What is much more important that "Get Prime x" (out of 12) does not show any error, while "Get Prime 1" shows 6 errors
• In Figure 2B, 3 columns are important: in Column H: (pm1+pm2)/2, in Column J: sqr(n) and in Column M: amin.
  A simple mental test shows, that in each row, for all values in these rows: (pm1+pm2)/2 = sqr(n) + amin.
  This means, because sqr(n) is 'given', that you only have to calculate amin, in order to calculate: (pm1+pm2)/2. And because pm1*pm2 is given, both pm1 and pm2 can be calculated.

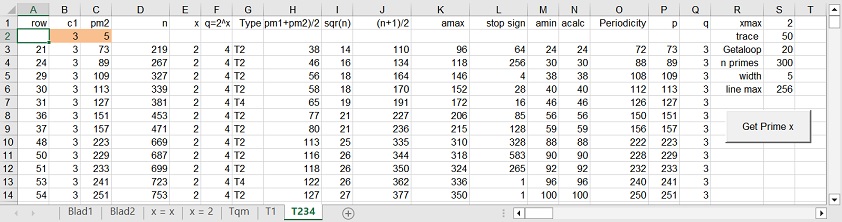
3. Spreadsheet layout: "T?"

Figure 3.1 "Get Prime x". pm1 = pm1 Figure 3.2 "Get Prime x". pm1 = c1

3.1 Operation spreadsheet: "T?"

The purpose of spreadsheet T? is to test in detail the "Calculating Periodicity in 5 easy steps" functionality to factorize the product n of two prime numbers pm1 and pm2. This functionality is identified as phase 1.
Important is the parameter n primes = 50, which shows that the total number of products n factorized is 50.

• In figure 3.1 the two prime numbers pm1 and pm2, and n are recalculated each time at the beginning of each factorization.
• In figure 3.2 only pm2 is recalculated at the beginning of each factorization. pm1 is constant. This controlled because the parameter pm1 is changed to c1.

3.2 Discussion

• Figure 3.1 demonstrates when both pm1 and pm2 are calculated each time. The first example calculated is 3 and 5. The last example calculated (not shown) is 233 and 239. Amin in all cases = 1.
  In all cases the factorization is performed with no error. That is why the type is indicated as a: ?
• Figure 3.2 demonstrates when pm1 = c1, and kept constant i.e. 3
  To use a constant value is what you can call: "The egg of Columbus" i.e., a simple solution for a complicated problem.
  In total the whole number of errors is 9 (out of 50). This are the combinations 3 with 73, 89, 109, 127, 151, 157, 223, 229 and 233.
  Figure 3.2 only shows the first 2 combinations.
• As mentioned in Figure 3.1 the value of amin is constant, and equal to 3. In Figure 3.2 the value of amin, linear increases from 1 to 95.
  However, in the lines with an error, the values of amin clearly show a dip.
  In line 21, with the prime numbers 3 and 73, amin is 6. The expected should be around 24.
  In line 24, with the prime numbers 3 and 89, amin is 8. The expected should be around 30.
  

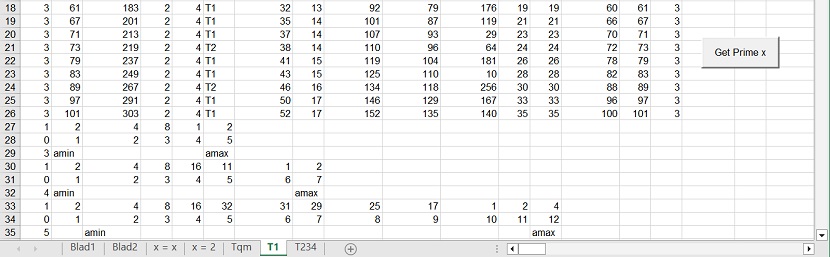
4. Spreadsheet layout: "T1"

Figure 4.1 "Get Prime x". pm1 = pm1

Figure 4.2 "Get Prime x". pm1 = c1

4.1 Operation spreadsheet: "T1"

The purpose of spreadsheet "T1" is to test in more detail the "Calculating Periodicity in 5 easy steps" functionality to factorize the product of two prime numbers pm1 and pm2. This is identified as: phase 2. The purpose of phase 2 is to solve a problem in the functionality identified as phase 1.

• In figure 4.1 the two prime numbers pm1 and pm2, and n are recalculated each time at the beginning of each factorization.
• In figure 4.2 only pm2 is recalculated at the beginning of each factorization. pm1 is constant. This controlled because the parameter pm1 is changed to c1.
• In figure 4.2 the bottom part shows the details, of the "Calculating Periodicity in 5 easy steps" functionality in three tests: for n = 15, 21 and 33.
  
  1. For n = 15, row 27 shows the so-called value x, which is equal to a^2 mod n. In this example x = a^2 mod 15.
     
     The function x(a) = a^2 mod 15 can also be written as: x(a+1) = x(a) * 2 mod 15.
  2. For n = 15, row 28 shows the value a; starting from 0.
     
  3. For n = 15, row 29 at column A shows the value 3, which is the row number of this example i.e., row 3.
     
  4. For n = 15, row 29 at column F shows amax. The value of "amax" is shown above amax in row 28 and has the value 5. "amax is calculated using (n+1)/2 - sqr(n).
     
  5. For n = 15, row 27 at column F shows the stop sign. This value is equal to x=5^2 mod 15 = 32 mod 15 = 2
     
  6. For n = 15, row 27 at column B also shows the stop sign. This value is equal to x=1^2 mod 15 = 2
     
  7. For n = 15, row 28 at column B shows amin. The value of amin = 1
     
  Using amin (pm1+pm2)/2 can be calculated. (pm1+pm2)/2 = sqr(n) + amin. This finishes the calculation of pm1 and pm2.

4.2 Discussion

As can be observed in Figure 3.1 the reason, why factorization does not work, lies in the calculation of amin. In all the cases when factorization is in error amin is too small. This are the rows 21 and 24.
The same can be observed in Figure 4.2. The rows in error are 21 and 24. To show this error, the Type is T2.

Amin calculation follows this logical scheme:

a = 0 : x = 1 p1: a = a + 1 : x = x * 2 'x(a+1) = x(a) * 2 If x > n then x = x - n If x = "stop sign" then amin = a : exit sub goto p1 Subroutine to calculate amin.

The problem is that in certain cases this test is stopped too early. The next occurrence of the "stop sign" should be used.
The actual subroutine used is: Geta_mod2_Int_array2. Two parameters: str_amin$ and Str_xn$ are added to initialize the two variables a and x mentioned in the above subroutine.

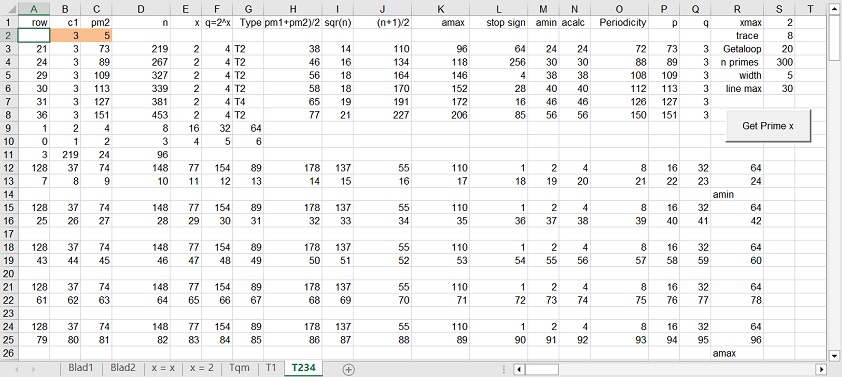
5. Spreadsheet layout: "T234"

Figure 5.1 "Get Prime x". pm1 = pm1

Figure 5.2 "Get Prime x". pm1 = pm1

5.1 Operation Spreadsheet: "T234"

The purpose of spreadsheet "T234" is to test in more detail the "Calculating Periodicity in 5 easy steps" functionality to factorize the product of two prime numbers pm1 and pm2. This is identified as: phase 2. The purpose of phase 2 is to solve a problem in the functionality identified as phase 1.
Infact, the program used in case of Spreadsheet T234 is exactly the same as Spreadsheet T1. The main difference that in case of T1 all the examples are displayed. In case of T234 only the lines in error are displayed. Type or error discovered are shown as T2, T3 and T4.
In order to calculate amin the stop sign has to be retrieved. However not always this value of amin works and the searching has to continue, and again. This results in the error types T2, T3, T4 etc. The combination pm1=3 and pm2 = 2113 shows the type T24.

5.2 Discussion

Both Figure 5.1 and Figure 5.2 almost show the same information. The difference is in the parameter line max.

• In Figure 5.1 line max = 256. The total number of values in each row = 256. That means all values, in each of the 3 rows that belong to one factorization, are stored one after one after. When amax is lower than 256 all the values are shown. When amax is higher than 256, all the values after 256 are not shown.
• In Figure 5.1 line max = 30. The value should be lower than 256. The exact value is not important.
  In this case all the values each of the 3 rows that belong to one factorization, are stored in different blocks of 3 rows. The dividing point is the stop sign.
  In Figure 5.1, the values of row 3 are stored in 6 blocks of 3 rows.
  Block 1 are the rows 9, 10 and 11. The dividing line is column G.
  Row 9, Column G, shows 64, which is the "stop sign". Row 10, Column 9, shows amin. In this case the value 6 for amin is wrong.
  The 4 values in row 11 are: 3 = Source row, 219 = n, 24 = amin and 96 = amax.
  Block 2 are the rows 12, 13 and 14. The dividing line is column R.
  Row 12, Column R, shows 64, which is the "stop sign". Row 13, Column R, shows amin. In this case the value 24 for amin is correct.
  Block 3 are the rows 15, 16 and 17. The dividing line is column R.
  Row 15, Column R, shows 64, which is the "stop sign". Row 16, Column R, shows amin. In this case both the "stop sign" and amin are not used.
  

The same type of information is also shown for all the 8 examples.

Reflection 1 - Phase 2

One of the main objective of phase 2 was to solve one error in the original program to simulate Shor's algorithm, which performs factorization on a quantum computer, on a digital computer. Already the effort to write the original program was a road of falling and getting up. One of the first discoveries was that Shor's algorithm on a quantum computer does not always work, assuming my understanding, for all values of n = pm1*pm2 on a quantum computer. The possible errors were identified as T1, T2, T3 and T4. The second step was to adept the algorithm such that it would work, preventing large internal numbers and preventing multiplications and divisions, with the object to make the program as fast as possible. This whole process goes in small steps. Often you think you have reached your goal, but additional testing showed that this was not true. A typical case is to write a program to take the square root, with array logic, to handle very large numbers. The final solution was what I called phase 1. The 'error' code was T?
In some sense I was lucky to identify the final solution with a: ?, assuming that it contained no errors. More testing revealed that the solution which I called phase 1, actual contained an error. First you get the feeling: again, what is wrong, why etc. The next step is to try to repeat the error using more examples and see what is common to all errors. Lucky again I soon found how to observe more errors, what the specific cause is and how to fix the error. Your nightmare disappears.
Still, this raises the question: is it possible using Shor's algorithm, to perform factorization, error free, on a Quantum Computer. I have my doubts. Even assuming that the Quantum Computer itself operates error free.

One of the lessons learned from this exercise is, that testing is a very important issue. The advantage of factorization the product of two prime numbers, is that you know the answer. If that is not the case, the results of any computational exercise have to be investigated very carefully. A typical case in point is artificial intelligence, specific if also intermediate results cannot be tested.

Reflection 2

Feedback

Back to my home page: Contents of This Document