Program "FindPrim" Benchmark Pentium P4 2.8 and Intel i5 M 460
Visual Basic, Visual Studio 2010 and Excel

To evaluate fatorization using Parallel processing select the following link:

Quantum Factoring Performance Evaluation - Using Parallel Processing - VB2010
Quantum Factoring Performance Evaluation - Using Parallel Processing - VB2019

The three programs evaluated are: FindPrim_array.xls, VB2010_FindPrim_PP and VB_FindPrim.

• FindPrim_array.xls is a program written in Excel
  Source Excel program: findprim.xls.zip This Zip file contains the two Excel programs: findprim shor.xls and findprim_array.xls
  For a description of how to operate the program "findprim shor.xls" select: findprim shor.xls.htm
• "VB FindPrim" is a program written in Visual Basic 5.0
  "VB Findprim.exe" file of program: VB exe.zip
• "VB2010 FindPrim PP" is a program written in Visual Basic 2010
  "VB2010 Findprim PP.exe" file of program: VB2010 exe.zip

The language structure of the three programs are basically identical. They are all derived from the Basic Language. The implementation details are different. Visual Basic 2010 is also capable to do parallel procesing.
The number to factorize n = 1230187600052977. The two prime numbers calculated are: 33478079 and 36746063

The results of the programs are stored in Table 1, Table 2 and Table 3
The left side of each table shows the results for the Pentium P4 processor. The right side shows the results for the intel processor.
The first line shows the results when x = 2. In this part the periodicity is calculated. Included is the GCD functionality in order to calculate the two prime numbers.
The second line shows the results when x = 5. The periodicity is not calculated because this is already done for x = 2. The GCD funtionality is included.
The results are shown in the columns 3 and 4.
The value 371 (589) in Table 1 is calculated uses array logic in double precision floating point format
The value 342 (435) in Table 1 is calculated uses array logic in long integer format
The values 371 and 56 are the same results as shown in: Shor's Algorithm - Cryptography

Excel Basic Benchmark

The above display shows the results of the Excel program "FindPrim_Array.xls" when you want to factorize the number n = 1230187600052977 with x from 2 to 10.
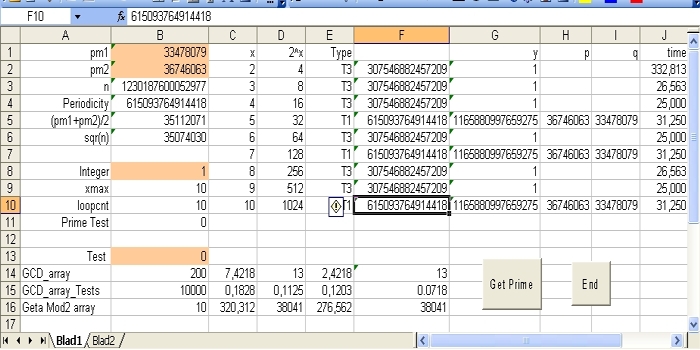
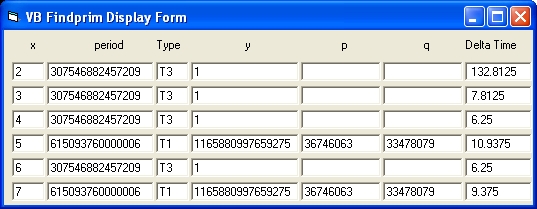
What the display in detail shows that this is only possible for the x values 5, 7 and 10.
The column at the right shows the time in ms. In the 3 cases of type T1 this is roughly 31 ms. That is not the time to factorize n = 1230187600052977, In real you have to add the time for x = 2 which is 332 ms. That is the time to calaculate the periodicity, which only has to be performed once.

Pentium P4 x = 2 T3 371 342 x = 5 T1 56 46 GCD_array 100 5,468 3,125 GCD_array_Test 1 10000 0,2984 0,2250 GCD_array_Test 2 10000 0,1234 0,0828 Geta_Mod2 10 271 273	Intel Core i5 M 460 @ 2.53 GHZ x = 2 T3 589 567 x = 5 T1 435 62 GCD_array 100 7,1484 5,7813 GCD_array_Test 1 10000 0,425 x GCD_array_Test 2 10000 16,093 x Geta_Mod2 10 464 473

Table 1: FindPrim_array.xls

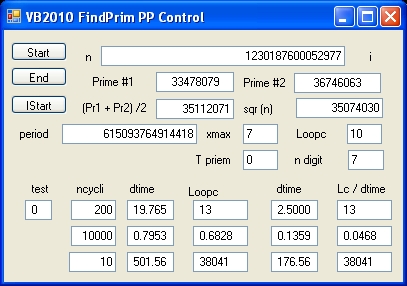
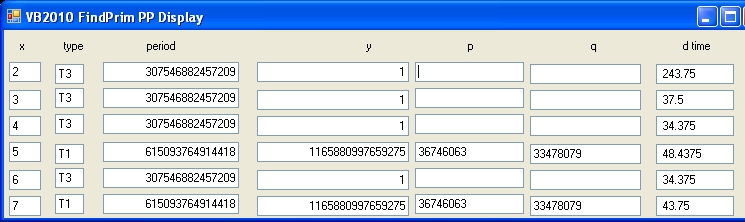
Visual Studio VB2010 Benchmark

Pentium P4 x = 2 T3 1314 232.8 x = 5 T1 446.8 35.9 GCD_array 100 19.765 2.500 GCD_array_Test 1 10000 0.7953 0.1359 GCD_array_Test 2 10000 0.6828 0.0468 Geta_Mod2 10 501.56 176.56	Intel Core i5 M 460 @ 2.53 GHZ x = 2 T3 1469 227.4 x = 5 T1 523.6 39 GCD_array 100 23.320 2.600 GCD_array_Test 1 10000 0.9084 0.1600 GCD_array_Test 2 10000 0.7802 0.0560 Geta_Mod2 10 572 166.2

Table 2: VB2010 FindPrim PP

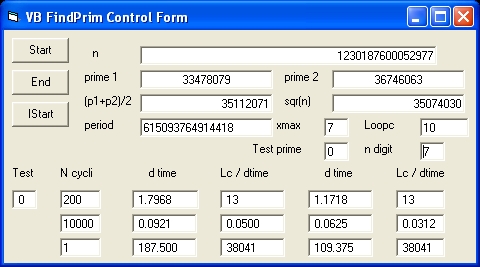
Visual Basic 5.0 Benchmark

Pentium P4 x = 2 T3 189 135.9 x = 5 T1 24.43 12.5 GCD_array 100 1.8750 1,1718 GCD_array_Test 1 10000 0.0953 0.0640 GCD_array_Test 2 10000 0.0515 0.0312 Geta_Mod2 10 156.250 109.375	Intel Core i5 M 460 @ 2.53 GHZ x = 2 T3 300 223.8 x = 5 T1 34.7 17.18 GCD_array 100 2.7539 1.7578 GCD_array_Test 1 10000 0.1402 0.0910 GCD_array_Test 2 10000 0.0750 0.0468 Geta_Mod2 10 230 187

Table 3: VB 5.0 FindPrim

Wat the above shows is:

• That the Pentium P4 2.8 is the fastest CPU compared with the Intel Core i5 when only one processor is used.
• That Visual basic 5.0 outperforms Visual Basic 2010 Express.

---

Feedback

None

---

Created: 25 October 2013
Updated: 21 September 2015

Back to my home page Contents of This Document