On the Electrodynamics of moving Bodies - by A. Einstein 1905 - Article review
This document contains article review "On the Electrodynamics of moving Bodies " by Albert Einstein written 1905
To order to read the article select:
http://users.physik.fu-berlin.de/~kleinert/files/eins_specrel.pdf
- The text in italics is copied from the article.
- Immediate followed by some comments
Contents
Reflection
Introduction - page 1.
-
The observable phenomenon here depends only on the relative motion of the conductor and the magnet, whereas the customary view draws a sharp distinction between the two cases in which either the one or the other of these bodies is in motion.
-
In the physical universe all objects are in motion and all motion is relative.
It is customary in an experiment to call one object at rest, implying that it stays at the same location relative to the enclosure of the laboratory, while the other one can be moving. Ofcourse from a more global perspective this is wrong.
-
-
-
Examples of this sort, together with the unsuccessful attempts to discover any motion of the earth relatively to the “light medium,” suggest that the phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest.
-
Both electrodynamics and mechanics involve motion, but it is tricky to treat them in one sentence because
they are physical completely different.
In both cases you first have to define what means "absolute rest" and why such a concept is important.
From a physical point of view throughout the Universe there are objects, and all these objects are more or less in motion. From a physical point of view all these objects influence each other, which makes a central approach (one coordinate system) the most obvious usefull. The whole of this description of moving objects does not require any electrodynamics, including light.
What is true that if an object emits a flash light, this flash will be emitted (localy) in all directions with the same physical speed, and that in return does not say anything about the speed of the object emitting the flash.
-
They suggest rather that, as has already been shown to the first order of small quantities, the same laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good.
-
When you study this sentence you must have a clear and detailed understanding what the laws of electrodynamics and what the laws (equations) of mechanics are. Infact you have to go one step deeper: you must first identify the underlying processes which both set of laws describe and secondly what the similarities are. If there are similarities then both can be described by the same laws. The differences by separate laws for each. The above sentence seems to exclude this.
Different reference frames imply different speeds. The question is to what extend physical processes are a function of speed. What the similarities and differences are between processes. The emphasis is on differences.
A different issue why mention the concept of frames (plural). The laws of physics will be much simpler if only one reference frame is used.
-
We will raise this conjecture (the purport of which will hereafter be called the “Principle of Relativity”) to the status of a postulate, and also introduce another postulate, which is only apparently irreconcilable with the former, namely, that light is always propagated in empty space with a definite velocity c which is independent of the state of motion of the emitting body.
-
Why introduce the concept of postulates? It is much more important to describe the experiments as detailed as possible which are the basis for these postulates.
Why calling the first postulate the "Principle of Relativity"? The word Relative makes only sense when from the physical point of view there is also something Absolute. It should be mentioned that all processes influence each other because always gravity is involved.
It is more usefull to assume that: "light propagates locally in all directions with the same speed.".
To demonstrate this by means of experiments is very difficult, because this implies that given two identical distances and two lightflashes (which start simultaneous) that the arrival times should be also simultaneous. To use atomic clocks could be the answer, but how to synchronise these clocks again makes this an almost impossible to solve problem.
See also: Reflection 1 - The speed of light.
-
-
-
-
-
-
-
-
-
-
-
-
Page 2
-
The theory to be developed is based—like all electrodynamics—on the kinematics
of the rigid body, since the assertions of any such theory have to do
with the relationships between rigid bodies (systems of co-ordinates), clocks,
and electromagnetic processes.
-
The kinematics of rigid bodies and rigid clocks versus electromagnetic processes are physical completely different and should be handled separately.
See also: Reflection 0 - Rigid Bodies & rigid standards of measurements
-
Insufficient consideration of this circumstance
lies at the root of the difficulties which the electrodynamics of moving bodies
at present encounters.
-
No detailed information is show what these "Insufficient considerations" are.
-
-
I. KINEMATICAL PART - page 2
1. Definition of Simultaneity - page 2.
-
In order to render our presentation more precise and to distinguish this system of co-ordinates verbally from others which will be introduced hereafter, we call it the “stationary system.”
-
Okay. Very good assumption to start our journey.
It should be mentioned that a system of co-ordinates only makes sense if it is linked to a physical object.
-
If a material point is at rest relatively to this system of co-ordinates, its position can be defined relatively thereto by the employment of rigid standards of measurement and the methods of Euclidean geometry, and can be expressed in Cartesian co-ordinates.
-
The defintion of "at rest" must imply that in due course the position of this material point does not change within this system of co-ordinates
See also: Reflection 00 - At rest
-
If we wish to describe the motion of a material point, we give the values of its co-ordinates as functions of the time.
-
This requires a definition of time and how time is measured.
To do that properly, you need one reference frame and clocks which are at rest (and synchronised) in this reference frame.
Time can only de defined as clock counts.
-
Now we must bear carefully in mind that a mathematical description of this kind has no physical meaning unless we are quite clear as to what we understand by “time.”
-
Time is defined as the counts of a clock at rest in this system of co-ordinates. In short time is defined as clock counts.
A second step is to define, for example: 10000 clock counts as 1 second, but that has no physical consequences.
-
-
-
If, for instance, I say, “That train arrives here at 7 o’clock,” I mean something like this: “The pointing of the small hand of my watch to 7 and the arrival of the train are simultaneous events.”
-
To define the "arriving time here at 7 o'clock as simultaneous events" is not practical. It is more realistic to call this one event. This makes it simpler to compare different events at different locations. In practice this means that we should define the arrival time with clock counts
-
It might appear possible to overcome all the difficulties attending the definition
of “time” by substituting “the position of the small hand of my watch” for
“time.”
-
That is correct, because than you link time with a position in space.
In practice it is more usefull to use "clock counts" as a substitute for "time" because both are physical different concepts but clock counts can directly be measured.
-
And in fact such a definition is satisfactory when we are concerned with defining a time exclusively for the place where the watch is located; but it is no longer satisfactory when we have to connect in time series of events occurring at different places, or—what comes to the same thing—to evaluate the times of events occurring at places remote from the watch.
-
This remark is correct. In fact each place where an event takes place requires its own clock.
In order to measure clock counts we will use a clock, which operates based on light signals.
The internal operation (geometry) of such a clock is not guaranteed to operate always the same when identical clocks are used under different physical situations.
-
-
-
We might, of course, content ourselves with time values determined by an
observer stationed together with the watch at the origin of the co-ordinates,
and co-ordinating the corresponding positions of the hands with light signals,
given out by every event to be timed, and reaching him through empty space.
-
Reading this line you can understand that Einstein is a clever man to write this up.
-
But this co-ordination has the disadvantage that it is not independent of the
standpoint of the observer with the watch or clock, as we know from experience.
-
This requires an explanation what is meant with experience.
-
-
-
-
Page 3
- If at the point A of space there is a clock, an observer at A can determine the
time values of events in the immediate proximity of A by finding the positions
of the hands which are simultaneous with these events.
-
The time of point A should be defined as the clock counts of clock A.
-
If there is at the point B of space another clock in all respects resembling the one at A, it is possible for an observer at B to determine the time values of events in the immediate neighbourhood of B.
-
-
We have so far defined only an “A time” and a “B time.”
-
Okay.
we have defined a point A with clock count A and a point B with clock count B
-
But it is not possible without further assumption to compare,
in respect of time, an event at A with an event at B.
-
This whole discussion depents about the concept "now". If there exists a "now" than both clock at point A and at point B should every moment indicate the same universal time "now" expressed in clocks counts.
-
-
-
-
-
We have not defined a common “time” for A and B, for the latter cannot be defined at all unless we establish by definition
that the “time” required by light to travel from A to B equals the “time” it requires to travel from B to A.
-
The first question to answer is what has the concept of time to do with light signals.
As a rule on clock counts should not be defined by definition.
clock counts should be established by means of experiment.
The problem with the above definition it is not clear if the above indicated experiment when repeated will reveal the same results. In principle both clocks involved can move in different directions within the system of co-ordinates.
What you can define is that the speed of light is the same in all directions within your system of co-ordinates.
Also that an object at rest does not move within your co-ordinate system. This can be a for example a clock at rest.
Also that a moving object moves (in time) within your co-ordinate system. This can be a for example a moving clock.
-
Let a ray of light start at the “A time” tA from A towards B, let it at the “B time” tB be reflected at B in the direction of A, and arrive again at A at the “A time” t'A.
-
'Okay' assuming clock counts are considered.
-
In accordance with definition the two clocks synchronize if
-
This is only true when the clocks are at rest.
-
Thus with the help of certain imaginary physical experiments we have settled what is to be understood by synchronous stationary clocks located at different places, and have evidently obtained a definition of “simultaneous,” or “synchronous,” and of “time.”
-
This is not an imaginary experiment. This should be a real experiment with the assumptions that all the objects, clocks involved are at rest.
-
-
-
-
-
In agreement with experience we further assume the quantity
|
2AB / (t'A - tA) = c,
|
(2) |
to be a universal constant—the velocity of light in empty space.
-
C expressed in distance defined by clock count.
See Reflection 2 - Paragraph 1 - Clock synchronization at rest.
-
-
-
It is essential to have time defined by means of stationary clocks in the stationary system, and the time now defined being appropriate to the stationary system we call it “the time of the stationary system.”
-
That is 100% Correct. Stationary meaning the same as at rest.
2. On the Relativity of Lengths and Times - page 3
It should be mentioned that at no place in the article the concept spacetime is used.
-
The following reflexions are based on the principle of relativity and on the principle of the constancy of the velocity of light. These two principles we define as follows:
-
Okay
-
-
Page 4
-
1. The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems of co-ordinates in uniform translatory motion.
-
Difficult to understand.
See also: Reflection 2 - Paragraph 1 The behaviour of moving clocks.
One of the major problems is that laws or models are descriptions of physical processes. Laws as such can have no influence on the processes they describe.
A whole different issue is if movement can have influence on the behaviour of a processes. When you consider electrical processes which are linked to objects the answer is: "yes". An electrical wire can issue an electrical force which can influence an magnetic object. The reverse is also true. An magnetic object can issue an magnetic force which can influence an electrical wire. In both cases movement is involved.
One specific problem is that in all types of movement always accelerations,in one way or the other, are involved.
In fact in any experiment always forces and gravitation are involved. To change the speed of a spaceship in empty space is impossible. Only by using galactic forces a spaceship can directly or indirectly increase or decrease its own speed or direction.
-
2. Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity c, whether the ray be emitted by a stationary or by a moving body.
-
The use of "" brackets implies a certain "uncertainty". The whole physical issue is that it is impossible to decide if the
body that emits the flash is at rest or moving in a "stationary" frame.
Consider two moving objects. There is a collision between these two objects. This collision creates a flash of light. This flash propagates in a sphere, centered around the point of collision. Is this point of collision at rest?
The problem is at the instant of the collision this point was physical part of both moving objects, which were both moving in different directions.
See for more information: Reflection 10 - The collision experiment.
-
Hence
|
velocity = light path/time-interval
|
(3) |
where time-interval is to be taken in the sense of the definition in 1. Definition of Simultaneity - page 2
-
In this case velocity is the speed of light, because a light-path is considered.
The dimensionality of the speed of light c is light-path divided by clock count.
To measure the speed of light by a stationary object or an object at rest is rather simple, because the lightpath is fixed.
To measure the speed of light by a moving object is much more difficult.
To verify that the speed of light is independent of the speed of the source is rather simple.
See: Reflection 1 - The speed of light.
-
Let there be given a stationary rigid rod; and let its length be l as measured by a measuring-rod which is also stationary.
-
That means only the rest frame is involved. Good practice.
It is interesting to know if the stationay rigid rod and the measuring rod have the same length. If that is the case, measuring is simple.
-
We now imagine the axis of the rod lying along the axis of x of the stationary system of co-ordinates, and that a uniform motion of parallel translation with velocity v along the axis of x in the direction of increasing x is then imparted to the rod.
-
First the velocity v of the rod in the rest frame should be calculated.
This is performed by placing a certain number of clocks along the path of the rod, which are all synchonized, and equally spaced.
The speed v of the rod is calculated based on the position of the front of the rod:
- The position xt1 and the time of the rod at t1 are measured.
- The position xt2 and the time of the rod at t2 are measured.
The speed of the rod "vrod1" is now calculated using the following equation:
|
vrod1 = (xt2 - xt1) / (t2 - t1)
|
(4) |
The dimensionality of vrod1 is distance divided by clock count.
-
We now inquire as to the length of the moving rod, and imagine its length to be ascertained by the following two operations:—
-
What is the reason of this question?
Probably the most common predicted answer is that the length is the same.
If it does not, as such, requires a physical explanation.
If an object moves away it appears shorter. This is also the case when the movement stops. In fact that it appears shorter is a vissible illusion.
If an object moves away it appears even shorter as strictly based on distance. When the movement stops the object becomes slightly longer. The reason is the speed of light.
-
(a) The observer moves together with the given measuring-rod and the rod to be measured, and measures the length of the rod directly by superposing the measuring-rod, in just the same way as if all three were at rest.
-
In case when the measuring-rod is of the same length as the rod to be measured, both will always be the same , when both are moved together. If there is any change in one, the other one will also change. (IMO)
-
(b) By means of stationary clocks set up in the stationary system and synchronizing in accordance with § 1, the observer ascertains at what points of the stationary system the two ends of the rod to be measured are located at a definite time.
The distance between these two points, measured by the measuring-rod already employed, which in this case is at rest, is also a length which may be designated “the length of the rod.”
-
A simpler experiment, IMO which tests the same, is :
- Consider two clocks at rest in the stationary system a distance l apart. The length of the rod as measured in the stationary system has the same length l.
Both clocks are started simultaneous (from a lightsignal at the center between the two clocks)
The moving clock moves towards the right. Near the two clocks is an observer.
When the front of the rod coincides with the clock at the right side the observer writes down the clock count. The observer at the left side does the same for the back end of the rod.
- When the numbers are the same there is no change in length involved. The two measuring events are simultaneous.
When the number in front is larger there is length contraction involved.
When the number in front is smaller there is length expansion involved.
The result is?
-
In accordance with the principle of relativity the length to be discovered by the operation (a)—we will call it “the length of the rod in the moving system”— must be equal to the length l of the stationary rod.
-
The only way to decide is by means of an experiment. Common sense predicts the same.
Why has the principle of relativity to be invoqued to make a point?
That these two concepts are the same does not validate the principle of SR.
-
The length to be discovered by the operation (b) we will call “the length of the (moving) rod in the stationary system.” This we shall determine on the basis of our two principles, and we shall find that it differs from l.
-
When the distance is not the same there must be a physical reason
-
-
-
-
-
-
-
Current kinematics tacitly assumes that the lengths determined by these two operations are precisely equal, or in other words, that a moving rigid body at the epoch t may in geometrical respects be perfectly represented by the same body at rest in a definite position.
-
That means there is no physical length contraction involved.
See also: Reflection 5 - Length contraction.
-
We imagine further that at the two ends A and B of the rod, clocks are placed which synchronize with the clocks of the stationary system, that is to say that their indications correspond at any instant to the “time of the stationary system” at the places where they happen to be. These clocks are therefore
“synchronous in the stationary system.”
-
That means that there are at the physical ends of the moving rod two moving clocks.
What the text indicates that the time of these two moving clock's show the same time if the positions of these clocks coincide which the position of clocks which run synchronous in the rest frame or stationary frame.
That is physical not true as show by experiments related to the twin paradox: moving clocks run slower.
-
We imagine further that with each clock there is a moving observer, and that these observers apply to both clocks the criterion established in § 1 for the synchronization of two clocks.
-
-
-
-
-
-
-
-
-
-
-
Page 5
-
Taking into consideration the principle of the constancy of the velocity of light we find
that
|
tB - tA = rAB/(c - v)
|
and
|
t'A - tB = rAB/ (c + v)
|
(5) |
where rAB denotes the length of the moving rod—measured in the stationary system.
-
It is not clear in this equation what is observed and what is measured.
See Reflection 3 - Paragraph 2 - Moving clock synchronization. for a critical discussion.
-
Observers moving with the moving rod would thus find that the two clocks were not synchronous, while observers in the stationary system would declare the clocks to be synchronous.
-
Again see above.
-
So we see that we cannot attach any absolute signification to the concept of simultaneity, but that two events which, viewed from a system of co-ordinates, are simultaneous, can no longer be looked upon as simultaneous events when envisaged from a system which is in motion relatively to that system.
-
Generally speaking what this means that you should only use one co-ordinate system.
See also: Reflection 4 - Conclusion.
-
-
3. Theory of the Transformation of Co-ordinates and Times from a Stationary System to another System in Uniform Motion of Translation Relatively to the Former - page 5
-
Let each system be provided with a rigid measuring-rod and a number of clocks, and let the two measuring-rods, and
likewise all the clocks of the two systems, be in all respects alike.
-
All the clocks can be mechanical alike, but if there is a set of clocks with a speed v1 and a different set of clocks with a speed v2 then they are not physical alike. The clock rate of one set relative towards the other set will be different. That is what twin type of experiments demonstrate.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
4. Physical Meaning of the Equations Obtained in Respect to Moving Rigid Bodies and Moving Clocks - page 9
This paragraph discusses Moving Rigid Bodies and Moving Clocks.
It is important to consider that moving clocks are also moving rigid clocks.
See also:
-
-
-
-
-
-
Page 10
-
-
-
A rigid body which, measured in a state of rest, has the form of a sphere,
therefore has in a state of motion—viewed from the stationary system—the
form of an ellipsoid of revolution with the axes
-
The emphasis is on the word viewed, which indicates a visible operation. This visible operation results in a observed change, but IMO has no physical consequences.
-
Thus, whereas the Y and Z dimensions of the sphere (and therefore of every
rigid body of no matter what form) do not appear modified by the motion, the
X dimension appears shortened in the ratio 1 : SQR (1-v^2/c^2)
, i.e. the greater the value of v, the greater the shortening.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Reflection 0 - Rigid Bodies - Rigid standards of measurement
Throughout the text the concept rigid body is used. Why this specific mention? See specific the text at Page 2
It is assumed that a clock is also a rigid object.
The problem rigid body can only be related to something physical.
That means:
- A reference meter stick (at rest in a stationary system of coordinates) and a rod of a certain length, are considerd of the same length, when put side by side and both ends coincide.
- A moving reference meter stick and a moving rod of a certain length, are also considerd of the same length, when put side by side and both ends coincide.
- A reference meter stick (at rest etc) and a moving rod of a certain length, are also considerd of the same length, when both ends coincide at the same clock count.
To perform this experiment requires two clocks (at rest etc) at both ends of the reference meter stick.
Both clocks are reset by means of a lightsignal, issued from a point midway between the two ends of the reference meter stick. The moving rod moves towards the right.
The clock at the right side of the reference meter stick should stop when its position coincides with the front end of the moving rod.
The clock at the left side of the reference meter stick should stop when its position coincides with the back end of the moving rod.
As mentioned before, both the meter stick and the moving rod are of the same length, when both clocks, after being stopped, show the same number of counts.
In all three cases the result of the experiment should be that the length of the rods are the same. In the cases 1 and 2 this is easy to accept. In case 3 this is more complicated because forces are introduced to start and stop the train. These forces should act instantaneous, over the whole length of the train, resulting that the whole train has always the same speed. That is what a rigid body means.
When a rod has the structure of a spring, it is easy to assume that the length of such a rod will increase when a force is applied at the front (in order to move the rod towards the right)
When a rod has the structure of a spring, it is also easy to assume that the length of such a rod will decrease when a force is applied at the back (in order to move the rod towards the right)
When a rod has the structure of a spring, it is also easy to assume that the length of such a rod will not change when a force is applied at the center (in order to move the rod towards the right)
The concept "Rigid standards of measurement" should not be confused with "Rigid Bodies".
- "Rigid Bodies" has to do with the physical condition of objects. As discussed above.
- "Rigid standards of measurement" has to do with a strict procedure of performing measurements
For more detail see: Reflection 5 - Length contraction.
Reflection 00 - At rest
The general tenet of this document is to start with the defintion of a system of coordinates, and a "stationary system". With in this "stationary system" we define a point at rest and a moving point.
The question is to what extend it is possible by means of any experiment to distinquish between these two
concepts.
Starting point is the considerating that the speed of light is the same in all directions, or is independent of the source and destination. This is explained in: Reflection 1 - The speed of light.
In order to establish that a clock is at rest perform the next experiment:
Place three identical clocks in front of you on a table, in such a way that the lightpath of the three is perpendicular towards each other.
Start a all the three clocks simultaneous.
Stop all the three clocks simultaneous
Make two observations: Of the clock count and of the direction of the lightpath.
- The clock count should be the same for all clocks.
- The direction of the lightpath should be the same for each clock compared with the initial set up.
If either one is not the case than the experiment is invalid.
Reflection 1 - The speed of light.
To establish that the speed of light is independent of the speed of an object is rather simple.
- First, you need a source which moves in a straight line through space and which at regular intervals emits, for example, a green flash. This is object A.
- Secondly, you need a source which also moves in a straight line through space and which at regular intervals emits, for example, a blue flash. This is object B.
- Consider a collision between object A and object B. This is the collision point P. Point P will emit an orange flash.
- Consider an observer C somewhere in space. Observer C observes at a certain moment a certain orange flash, and almost simultaneous an green and a blue flash. In principle this can also be simultaneous, but that depends how close before the collision i.e. the emission of the orange flash, object A actual did emit a green flash and object B actual did emit a blue flash.
You can perform the same experiment with all different speeds of A and B and with all different angles between the two objects but generally speaking observer C will always observe (more or less) the same.
The only conclusion is that the (local) speed of light is independent of the source and destination, but that does not answer the question what the speed of light is.
The calculation of the speed of light c is described at: page 3 .
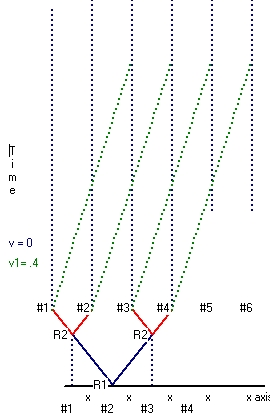
Reflection 2 - Paragraph 1 - Clock at rest synchronization.
The problem with equation 2 (repeated below) is that it is not clear exactly what is measured as a result of an experiment versus what is calculated.
|
2AB / (t'A - tA) = c.
|
(2) |
What the experiment shows are the measurements of three events tA, tB and t'A based on a fixed distance AB.
Using these results we can perform two calculations.
|
c1 = AB/ (tB - tA)
|
and
|
c2 = AB/ (t'A - tB)
|
What this experiment assumes is that the speed of light in both opposing directions is the same. When that is the case c1 = c2 = c. Both equations can now be used to calculate the speed of light.
An almost similar experiment can be set up with a point A in between the points B and B' such that BA = AB', all in a straight line.
In this new experiment a lightsignal will be emitted at a point A at moment tA in both directions. These two signals will be detected at point B at moment tB and at point B' at moment t'B.
The two calculations which describe this experiment are:
|
c1 = BA/ (tB - tA)
|
and
|
c2 = AB'/ (t'B - tA)
|
Because c1=c2=c and BA=AB' we get: tB = t'B. That means tB and t'B are simultaneous.
The two signals each can be used to reset a clock, which thereafter will run synchronous. .
The same methodology can be used to synchronize any number of clocks at rest.
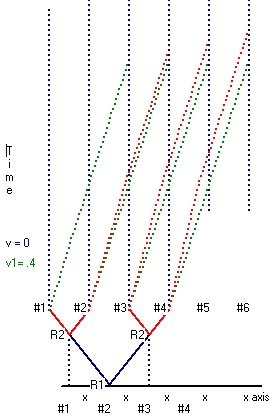
Reflection 3 - Paragraph 2 - Moving clock synchronization.
The problem with equation 5 (repeated below) is that it is not clear exactly what is measured as a result of an experiment versus what is calculated.
|
tB - tA = rAB/(c - v)
|
and
|
t'A - tB = rAB/ (c + v)
|
(5) |
What can be calculated are the two equations:
|
cv1 = rAB/ (tB - tA)
|
and
|
cv2 = rAB/ (t'A - tB).
|
It should be mentioned that both speeds cv1 and cv2 are not physical quantities but calculated quantities.
Using the following two equations with the previous calculated values of c and v:
|
cv1 = c - v
|
and
|
cv2 = c + v
|
both equations can be validated, including equation (5).
An almost similar experiment can be set up with a point A in between the points B and B' such that BA = AB', all in a straight line.
In this new experiment a lightsignal will be emitted at a point A at moment tA in both directions. These two signals will be detected at point B at moment tB and at point B' at moment t'B.
The two calculations which describe this experiment are:
|
cv1 = BA/ (tB - tA)
|
and
|
cv2 = AB'/ (t'B - tA)
|
Because cv1 <> cv2 and BA=AB' we get: tB <> t'B. That means tB and t'B are not simultaneous relative to a frame at rest.
The two signals each can be used to reset two clocks, which thereafter will run synchronous relative towards each other.
These clocks will not run simultaneous relative to clocks at rest, but slower
See also: Reflection 4 - Conclusion.
Reflection 4 - Conclusion.
The definition of "the laws of nature" accordingly to Wikipedia
(See https://en.wikipedia.org/wiki/Scientific_law ) reads:
"A scientific law is a statement based on repeated experiments or
observations that describe some aspect of the natural world."
What that means in order to unravel the "laws of nature" we should perform experiments.
Reflection 2 - Paragraph 1 - Clock at rest synchronization. describes how to synchronize two clocks in a system at rest.
This is done by transmitting a flash of light starting from a common point A towards to points B and B' such that the distance AB and AB' are the same. Using the assumption (postulate) that the speed of light is the same in both directions the two flashes will reach both points B and B' simultaneous.
Those two flashes can now be used to reset two clocks in a system at rest. The same methodology can be used to synchronize any number of clocks in a system at rest.
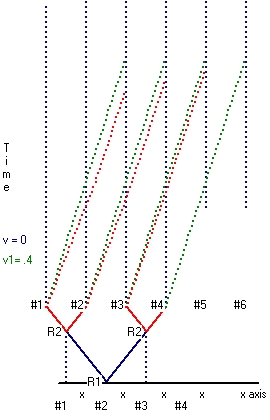
Reflection 3 - Paragraph 2 - Moving clock synchronization. describes how to synchronize two moving clocks.
Starting point is a straight line. Along the whole line clocks are placed. The distance between two adjacent clocks is l. All the clocks are at rest and synchronized as described in paragraph 2.
The experiment is performed with a rod of length l. The initial position of the rod is in between two clocks. The rod also has two clocks: one in front and one in the back. Both clocks are synchronized with the clocks at rest.
The experiment performed is similar as a twin paradox type experiment. From a functional point of view the rod is like a spaceship with an engine.
Experiment 1 involves a number of phases:
- The engine is started and slowly the rod is brought to speed v.
- The engine is stopped and the rod will travel a certain distance with constant speed v.
- After a certain time the engine is set in reverse direction in order to stop the rod.
- The speed of the rod in forward direction decreases until zero
- Now the rod starts to move in the opposite and the speed starts to increase until the same speed v.
- The engine is stopped and the rod will travel with constant speed v.
- After a certain time the engine is set in reverse direction in order to stop the rod.
- The speed of the rod in forward direction decreases until zero.
- This terminates the experiment with the rod exactly at the same position as at the beginning of the experiment.
After the trip two important things will be observed:
- The reading of the 'moving' clock in the front of the rod does not coincide with the clock at rest. There is an offset. The # of counts of the moving clock is lower than the # of counts of the clock at rest.
- What is important that the moving clock in the back, exactly shows the same behaviour. The offset is the same as the clock in front
What this means is that the physical behaviour of both clocks is the same. They both are synchronized.
During the trip also someting important can be observed:
- Immediate when the position of the front of the moving rod coincides with a clock at rest an observer at the front sees that his moving clock runs slower than the clock at rest. There is an offset.
- The same for an observer at the back of the rod. The offset in the back is the same as the offset in front.
- What is also important that during phase (2) the accumulated offset increases linear
- During phase (3) that the accumulated offset increases less because the offset decreases (i.e. the speed of the moving rod decreases)
The reason is because the behaviour of both clocks is physical the same. That means both clock run synchronized relative towards each other and both run slower relative towards the clocks at rest.
It also means that all the ticks of the clocks at rest are simultaneous events. The same for all the ticks of the moving clocks. The ticks of a clock at rest compared to a moving clock are not simultaneous events.
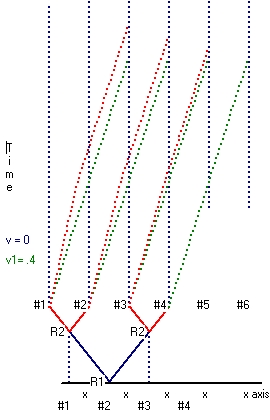
However the same experiment can also be used to learn more. This is what I call experiment 2:
- Consider phase (2) in the above experiment. In that case the rod moves forward with two clocks which are already are synchronized. The engines are off. From the point of view of an observer the rod is at rest and the two clocks are at rest.
- Again along the whole line clocks are placed. The distance between two adjacent clocks is l. Using the same concept as explained in paragraph 1 we can synchronize all these clocks with the clocks attached to the rod considered at rest.
(It is simpler to consider the first set of clocks as below the rod and this second set of clocks as above the rod)
- The next thing we do is, the same as in phase (3) in experiment 1, we start the engine. However not to stop the rod which has a physical speed v in experiment 1, but to start the rod, which from the point of view of the observer is at rest, to accelerate until we reach a certain speed v.
- Immediate when the observer at the front of the rod reaches a clock at rest (the clocks above us) we observe something very interesting: There is an offset between the clock at rest and the moving clock attached to the rod, however now the moving clock runs faster than the clock at rest, and not slower as in experiment 1
The reason is physical.
- In experiment 1 we started from a physical state at rest. In that case in the initial situation
both clocks at rest are running fast and have a speed v= 0. When you start the engine, the speed of the moving clock increases. Its path length increases and the clock runs slower.
- In experiment 2 we started from a physical state in which both clock are moving, which we called at rest. In that case in the initial situation, both clocks 'at rest', are running slow and have a physical speed v > 0. When you start the engine, physical the speed of the moving clock decreases. Its path length decreases and the clock runs faster.
In short the clock which in absolute sense is at rest runs the fastest. All other clocks run slower.
For more detail information select:
Reflection 5 - Length contraction.
Is there any form of length contraction involved in the behaviour of (moving) clocks?
In Reflection 3 - Worldline Perpendicular Mirrors - Twin Paradox the equation which describes the moving clock as t1=t0/(1-v2/c2).
In Reflection 4 - Worldline Parallel Mirrors - Rocket experiment the equation which describes the moving clock as t1=t0/sqr(1-v2/c2).
That means the behaviour is different.
To make the performance the same length contraction can be introduced in the first case. As such we get: t1=t0/(1-v2/c2) * sqr(1-v^2/c^2) = t0/sqr(1-v^2/c^2). The question is: Is this physical allowed?
Assuming you start with two clocks at rest. The reason why the behaviour of a moving clock compared to a clock at rest is different is because, in any experiment, forces are required to move the clock and secondly because additional forces are required to bring the clock to its original starting position and again at rest. These forces indirectly can also influence the performance of the clock.
To test the actual performance a real experiments have to be performed. A thought experiment is not enough.
Details about how to test moving clocks is described in Appendix 2. As such:
- One type with the mirrors perpendicular in the direction of movement
- One type with the mirrors parallel to the direction of movement.
Starting point should be a frame with clocks at rest, synchronized in the way discussed in Appendix 2.
It does not matter which type of clocks are used as 'at rest' because these clocks have no speed and as such the performance is the same.
One thing that is very important is that the clocks should move in a straight line, because any movement will change the alignment of the mirrors. This makes it almost impossible to test the behaviour in reality.
Along the same line at the end of the experiment (when the two rods used should meet each other at the end of the trip) the aligment of the light signal should be tested.
- When the mirrors are perpendicular the light signal should be horizontal.
- When the mirrors are parallel the light signal should be vertical.
In short the condition of the lightsignal should be the same before and after the trip. This extremely difficult when the clock is not moved in a straight line.
Experiment to chalenge Length Contraction
Consider two rods with each 4 clocks with the mirrors parallel, light signal vertical
Synchronization is performed as described in Appendix 2.
The 4 clocks in the rod at rest are described as A1, A2, A3 and A4 (at the right)
The 4 clocks in moving the rod are indicated as B1, B2, B3 and B4 (at the right)
In the above two different possibilities in length contraction and one possibility in length expansion is indicated. The question is what will happen in reality? Only a real experiment can decide.
What is important that length contraction only affects the behaviour during acceleration and not there after.
But suppose there is length contraction. This length contraction will affect all moving rods equaly (as a function of speed). This is the point of the different types of length contraction discussed above. Also all clocks are affected in some way, independent of the physical construction of the rod.
At the same time it is also true that a clock with perpendicular mirrors will be affected more than a clock with parallel mirrors. As a result the distance between the mirrors will decrease and the clock will start to run faster. This will offset the slower ticking rate, induced when there is no length contraction, and the rate in both cases could be the same.
Actual performed experiments should demonstrate if that is the case.
It should also be mentioned that physical length contraction and the length of the light path are two complete different subjects and have nothing to do with different reference frames, but instead with different physical speeds of the objects involved.
If you want to give a comment you can use the following form Comment form
Created: 19 August 2019
Modified: 27 August 2019
Modified: 30 December 2019
Go Back to Article Review
Back to my home page Index