Comments about the book "The Evolution of Scientific thought from Newton to Einstein" by A. d'Abro
This document contains comments about the book: "The Evolution of Scientific thought from Newton to Einstein" by a. d'abro. Dover Publications 1950
- The text in italics is copied from that url
- Immediate followed by some comments
In the last paragraph I explain my own opinion.
Preface - Of the Comments
Contents
Reflection
Foreword - page 9
-
-
-
-
Page 16
-
Long before the advent of Einstein, problems pertaining to the relativity of motion through empty space had occupied the attention of students of nature.
-
In order to understand this sentence, that means to discuss certain issues, first you have to define the difference between absolute versus relative motion and empty versus non empty space.
As a sort of postulate you could start with this introduction:
-
The total universe, the whole world, consists of physical objects. The area between these objects we call (empty) space. etc.
At the end of the page we read:
-
There were some who held that empty space, and with it all motion, must be relative; that states of absolute motion or absolute rest through empty space were meaningless concepts.
-
If absolute motion and absolute rest don't exist they can never be properly defined and should not be used. Only the concepts motion and rest should be used.
This is a philosophical issue.
See also Reflection 4 - Absolute versus relative in Newton (Classical) versus Einstein.
Page 17
-
-
-
All these views were in full accord with our visual perceptions and they were expressed by what is known as the visual or kinematic principle of the relativity of motion.
-
Motion is always observed in relation with the changing distance between at least one other object.
To use the term absolute and relative only makes sense if a clear distinction between the two exists.
-
-
-
Now it is to be noted that notwithstanding the absolute nature which Newton attributed to all states of motion and of rest in empty space, a certain type of absolute motion called Galilean * or again uniform translationary motion (defined by an absolute velocity but no absolute acceleration) was recognised by him as being incapable of detection, so far as experiments of a mechanical nature were concerned.
-
This whole line of reasoning is only true in principle but not in practice, because acceleration can be detected by means of mechanical experiments.
-
This complete irrelevancy of absolute or absolute Galilean motion to mechanical experiments was expressed in what is known as the Galilean or Newtonian or classical or dynamical principle of the relativity of Galilean motion through empty space.
-
Empty space does not exist.
-
-
-
-
-
-
-
-
Page 18
-
-
-
-
-
When the Newtonian principle of relativity was extended in this way it became Einstein's special principle of relativity.
-
-
-
-
-
-
-
-
-
-
-
-
-
Chapter 1.
Manifolds - page 23
-
An aggregate of such continuous sensations constitutes what is called a sensory continuum or continuous manifold.
-
It is tricky to start a discussion based on human senses, because they are subjective.
-
That continuity is a concept which springs from experience can scarcely be doubted and it can be accounted for by the ability of our crude sense to differentiate between impressions which are almost alike.
-
Our crude senses can be highly misleading and can be different for different people.
-
-
Page 24
-
In the case assumed we should be dealing with a two-dimensional continuum or continuous manifold of sounds; etc for us to designate it by two numbers, one specifying its pitch and the other its intensity.
-
A manifold is a two-dimensional plane.
-
-
-
-
Page 26
-
When we seek to determine the dimensionality of perceptual space, it self a sensory continuum produced by the superposition of the visual, the tactual and motive continua, the problem is more difficult.
-
First this requires a definition of what dimensionality means.
-
It would be found, however, that perceptual space has three dimensions; but as the necessary explanations would require several chapters we must refer the reader to Poincaré's profound writings for more ample information.
-
The issue is much more physical space than perceptual space. Perceptual space is human based. Physical space is human independent.
-
Summarising, we may say that our belief in the tri-dimensionality of space can be accounted for on the grounds of sensory experience.
-
The three dimensions of space is not a belief. It has nothing to do with what we humans do. It is physics.
See also: Reflection 7a - Physical dimensionality versus Mathematical dimensionality.
Page 28
-
But the inherent inconsistencies which endure in all sensory continua constituted a still more important reason for compelling mathematicians to idealise perpetual space.
-
In some sense mathematics, which is about numbers, and space, which is about physics are very difficult to unite, to treat on equal footing.
-
In a sensory continuum, as we have seen, a sensation A cannot be distinguished from its immediate successor, the sensation B; neither can B be differentiated from C. Yet no difficulty is experienced in differentiating A from C.
-
In real if all these sensations are experienced at the same positions but at different times then it should be possible to experience each in some sort of logical order, other wise they cannot be distinguished.
See also page 71
See also Reflection 2 - Sensory continuum.
-
-
-
-
-
-
Page 29
-
-
-
-
-
-
-
In this way mathematicians obtained what is known as Grand Continuum, or Mathematical Continuum
-
Okay
-
-
-
-
-
-
Page 30
-
-
-
Let us suppose, then that we have conceived of a three-dimensional mathematical space, obtained as an abstraction from the three-dimensional space of common experience.
-
The problem is that what we experience is not the reality. What we experience is only the local reality.
What we experience is only a very small part of the universe in the past.
-
-
-
-
-
-
Chapter 2.
The birth of Metrical Geometry - page 32
-
-
-
-
Page 33
-
-
-
-
In this chapter the two concepts postulates and axioms are discussed. For more detail see: Reflection III - The philosophy of Science. Experiments and Postulates.
An important point to study science is to make a clear difference because what we call physics and what we call mathematics. Physics is the study of all what exist in the physical world. Postulates are the simplest concepts which are used to describe the physical world. Mathematics is the world of geometrical structures, equations and numbers.
Axioms are the most simple concepts which are use to study mathematics.
It is important because for example the Parallel Postulate belongs to mathematics and should be called Parallel axiom See also: page 35
|
-
One private perspective with its converging rails taken by itself and considered without reference to other perspectives could not contain sufficient data to enable us to conceive of three-dimensional space, homogeneous and isotropic.
-
It is very difficult from our perspective to declare the physical universe as being homogeneous and isotropic. See also: page 49
See also: Reflection 1 - Observers, humans and light.
-
-
-
-
-
-
Page 34
-
-
-
It professes to teach us that the sum of the three angles of a Euclidean triangle is equal to 180 degrees and not a fraction more or a fraction less.
-
This is only true in a flat 'horizontal' plane.
-
Obviously no empirical determination could ever lay claim to such absolute certitude.
-
The 180 degrees is not something absolute, but something exact by definition.
-
-
-
-
-
-
Page 35
-
-
-
-
-
To make a long story short, it was found by varying one of Euclid's fundamental assumptions, known as the Parallel Postulate, it was possible to construct two other geometrical doctrines, perfectly consistent in every respect, though differing widely from Euclidean geometry.
-
Okay.
-
These are known as the non-Euclidean geometries of Lobatchewski and of Riemann
-
-
Euclid's parallel postulate can be expressed by stating that through a point in a plane it is always possible to trace one and only one straight line parallel to a given straight line lying in the plane. Lobatchewski denied this postulate and assumed that an indefinite number of non-intersecting straight lines could be drawn, and Riemann assumed that none could be drawn
-
The issue is here strictly mathematical, that is why the B>Parallel Postulate should be called B>Parallel Axiom
-
Thus, whereas in Euclidean geometry the sum of the angles of any triangle is always equal to the two right angles, in non-Euclidean geometry the value of the sum varies with the size of the triangles.
-
In the physical world the sum of the angles of any triangle is always equal to the two right angles assuming the triangle is constructed on a flat surface.
The question is if the non-Euclidean geometry also applies to the physical world.
-
It is always less than two right angles in Lobatchewski's and always greater in Riemann's
-
Okay.
-
-
-
-
-
-
-
-
-
-
Page 36
-
The character of self-evidence which had been formerly credited to the Euclidean axioms was seen to be illusory.
-
You need more detail to understand this, specific which Euclidean axioms are at stake. Anyway the word 'illusory' is tricky.
For more about self-evident see also: page 37
-
-
-
To illustrate this point more fully, let us assume that we think we know what is implied by a straight line.
-
This is typical a different issue, compared mathematical versus physical.
-
Whether we merely imagine a straight line or endeavour to realise one concretely, we are always faced with the same difficulty.
-
Mathematical a straight line is always a line on a piece of paper. Physical it is a connection between two points i.e. a rod.
-
But whatever method we adopt, it is apparent that our intuitive recognition of straightness in any given case will always be based on physical criteria dealing with the behaviour of light rays and material bodies.
-
This is all physical. Of course you have to be very carefully when considering light rays.
-
We may close our eyes and think of straightness in the abstract as much as we please, but ultimately we should always be imaging physical illustrations.
-
This is a tricky sentence. Straightness is a different issue for physical objects versus mathematical illustrations (drawings)
-
Suppose, then, that material bodies, including our own human body, were to behave different when displaced.
-
?
-
If corresponding adjustments were to affect the paths of light rays, we should be led to credit rigidity to bodies which from the Euclidean point of view would be squirming when set in motion.
-
The behaviour of light rays around material objects is strictly a physical issue and has nothing to do with Euclidean versus non-Euclidean (which is mathematical)
-
As a result, our straight line, that is, the line defined by a stretched rope, our line of sight, the shortest path between to points, would no longer coincide with a Euclidean straight line.
-
The line defined by a stretched rope is never straight. It is always bended by its weight.
Our line of sight can also be physical bended.
The shortest path between two physical points on the surface of the earth is always bended.
-
From the Euclidean standpoint our straight line would be curved, but from our own point of view it would be the reverse: the Euclidean straight line would now manifest curvature both visually and as a result of measurement.
-
This whole discussion is tricky because there is a mix between mathematical issues versus physical issues.
What makes the discussion also difficult, if there is a mix of Euclidean issues versus non-Euclidean issues?
-
-
-
Page 37
-
Incidentally, we are now in a position to understand why the Euclidean axioms appeared self-evident or at least imposed by reason.
For more about self-evidence see also: page 36
-
-
They represented mathematical abstractions derived from experience, from our experience with light rays and material bodies among which we live.
-
What this experience tells us that the path of a light ray is not always straight but can be bended and this bending is a function of the mass involved.
This bending has nothing to do with the mathematical concept Euclidean versus non-Euclidean.
-
For the present, let us note that since our judgment of straightness is contingent (depending) on the disclosures of experience, even the geometry of the space in which we actually live cannot be decided upon a priori.
-
We live in physical space.
-
To a first approximation, to be sure, this geometry appears to be Euclidean; but we cannot prophesy what it may turn out to be when nature is studied with ever-increasing refinement.
-
What is the type of experiment that demonstrates that geometry is Euclidian, and what should be the result, to conclude that in a certain case the geometry is non-Euclidian.
Remember the surface of the earth is not flat and non-Euclidean but that says nothing about physical space.
-
-
-
-
-
-
-
-
-
-
-
-
Such discussions might have appeared to be merely academic a few years ago; and non-Euclidean geometry, though of vast philosophical interest, might have seemed devoid of any practical importance.
-
It is important to remember that we live in a physical world.
-
But to-day, thanks to Einstein, we have definite reasons for believing that ultra-precise observation of nature has revealed our natural geometry arrived at with solids and light rays to be slightly non-Euclidean and vary from place to place.
-
The most important question is answer is when a light ray does not follow a straight path around matter; does that mean that the universe is (partly) non-Euclidean?
The issue is more complicated, because the force of gravity itself follows a straight path.
-
A more thoroughly study of Euclid's axioms and postulates proved them inadequate for the deduction of Euclid's geometry.
-
More detailed information is required to back up this sentence.
-
-
-
-
-
-
-
-
-
-
-
-
-
Page 38
-
Likewise, it was proved possible to posit a system of postulates which would yield Euclidean and non-Euclidean geometries of any number of dimensions; hence, so far as the rational requirements of the mind were concerned, there was no reason to limit geometry to three dimensions.
-
Our mind has nothing to do with this. The issue is what mathematical possible versus physical. In a mathematical sense you can consider mathematical space with much more than 3 dimensions. In physical sense physical space and physical objects are limited to three dimensions.
Physical space, specific the objects within, can change in position in time. To make this visible you need a video camera. -
-
-
From all this rather long discussion on the subject of postulates and axioms we see that the axioms or postulates of geometry are most certainly not imposed on us a priori in any unique matter.
-
Why mention this. The science of mathematics is based on very strict logical rules. Science is based on concepts. A set of fundamental concepts we call axioms. Starting from these axioms and using the logical rules additional concepts can be derived. In principle it is possible to replace all our axioms by a more fundamental set of concepts.
In the physical world the same is the case with postulates in stead of axioms.
-
We may vary them in many ways and, as regards real space, our only reason for selecting one system of postulates rather than another (hence one type of geometry in preference to another) is that it happens to be in better agreement with the facts of observations when solid bodies and light rays are taken into considerations.
-
Specific here it is important to make a clear with physics versus mathematics and postulates versus axioms.
In the physical world light rays are bended, which can be established by physical experiments. This has nothing to do with mathematics and the explanation is purely physical in the same sense as the trajectories of the planets around the Sun are also bended.
This has nothing to do for example with the Parallel Postulate or better the Parallel axiom.
-
-
Chapter 3.
Riemann's Discoveries and Congruence - page 39
-
-
-
By congruence we mean the equality of two distances and more generally of two volumes in space.
-
Okay.
-
-
-
-
-
-
-
-
-
-
-
-
Page 45
-
-
-
-
-
-
-
As a matter of fact it would be totally impossible for us to discover exactly what distance the earth had travelled.
-
That is too strong wording. The issue is, are there method's to improve the accuracy with which this is done.
-
-
-
-
Chapter 4.
The Problem of Physical Space - page 47
-
Mathematical space is amorphous; it posses no intrinsic metrics and our choice of standards of measurements is largely arbitrary.
-
Mathematical space is neither empty nor amorphous. Mathematical space is not something that physical exists. Mathematical space can contain mathematical objects or models.
All of this belongs to mathematics. See also page 455
Next sentence:
-
As a result, absolute shape, size and straightness are meaningless concepts.
-
To use the word absolute for any physical object seems irrelevant. The only exception is that the standard used, to perform a measurement, could be called: absolute.
-
So here, it appears that there exists an important difference between mathematical space, where no particular definition of congruence is suggested and physical space. In physical space a definite type seems to impose itself naturally and is accepted unanimously.
-
The purpose of science is to study the evolution of the physical world, not so much of physical space but the behaviour of the objects within.
That means to describe everything as detailed as possible.
Such a physical description can be in the form of a written language, a part of which can be in the form of a mathematical language.
In case when mathematics is used (specific when measurements are involved) a clear link with what is physical meant should be defined.
IMO concepts like mathematical space have there own limitations compared to physical space.
-
-
-
-
Page 48
-
This physical definition of congruence may be termed practical congruence, as distinguished from theoretical congruence, which is embodied by the mathematical types we have discussed.
-
Okay
-
-
-
We may also recall that his rigid bodies having been defined, the definition of a straight line as the axis of rotation of a revolving solid, two of whose points are fixed, or as the shortest distance between two points in space, follows immediately; and of course the straight line thus defined satisfies Euclid's parallel postulate, since it is derived from the behaviour of Euclidean solids.
-
Okay.
-
-
-
-
-
-
Page 49
-
All we can say is that the principle of sufficient reason compels us to credit empty space with a sameness throughout, and that our measuring rods and material bodies must also behave homogeneously and isotropic, as indeed they do in the three geometries discussed.
-
-
-
-
Only if measurements undertaken with our rods in different parts of space yielded variable non-homogeneous numerical results should we have to assume that space was not really empty and that our rods were subject to local influences.
-
This is the case in real experiments.
-
-
-
Of course, in an attempt of this sort, measurements with material rods were out of the question and it was necessary to appeal to other methods of exploration.
-
Okay. Next:
-
These were obtained by taking advantage of the propagation of light rays in empty space.
-
How is that discovered? Does the writer have secret knowledge?
-
It was known that over the limited extensions of ordinary experience the paths of light rays coincided with the straight lines determined by rods or stretched strings, so that rays of light could be used in place of stretched strings or rods for the purpose of defining geodesics.
-
No you can not. The issue is first what determines when or when not rods can be used to determine straight lines. The next issue is: what is the boundary condition that defines if a line is straight versus bended,
and finally are light rays any better to be used than rods.
-
Triangulations effected with light rays should there fore yield the same results as measurements performed with rods and should reveal the geometry of space with as much accuracy as would the more conventional kinds of measurements.
-
When the results are the same the accuracy is the same. The question is, are the results the same.
Page 50
-
-
-
Yet the most refined astronomical measurements of stellar parallaxes failed to reveal the slightest trace of non-Euclideanism.
-
That is interesting. The issue is can non-Euclideanism be something very local? Something for example very close to a Black Hole?
-
-
-
And yet, when we submit all these various examples to a critical analysis, we cannot help but see that this determination of the geometry of space is essential physical and is therefore contingent on the behaviour of material objects and the rays of light.
-
- The first question to answer is what is the geometry of space assuming that space is completely empty i.e. that there are no objects in space.
The answer in that case could have been: strictly Euclidean.
But what does that mean?
- The next question to answer is: does the geometry chance when we add a finite number of set of objects into this universe? (One set of objects being one Galaxy).
I doubt that. All the objects will fall freely through space, 'guided by gravity' i.e. each object guided by the influence of all the other objects.
- Does the behaviour of the objects have anything to do with the behaviour of light rays?
No.
|
-
And we may well wonder what the behaviour of physical objects should have to do with the geometry of space.
-
With empty space nothing. The question in general cannot be answered.
-
However, regardless of what opinions we may eventually defend on the subject of geometry, intrinsic to physical space; it can scarcely be held that this last argument of the critic proves his point in the slightest degree.
-
It is doubtful if physical empty space has any intrinsic geometry.
What does intrinsic geometry mean? Does this imply some sort of structure? I doubt that.
Page 56
-
-
-
-
-
-
-
-
-
Expressed in a different way, real space appears to be permeated by an invisible field, the Metrical Field, endowing it with a metrics or structure
-
Why mention the word: invisible? An important issue is: fields are considered pure mathematical. However can a field also be something physical?
Maybe the reasoning is like: forces are physical, fields are mathematical.
Anyway this sentence is complicated because of the words 'permeated', 'endowing', 'metrics' and 'structure'.
-
-
Page 58
-
-
-
-
-
-
-
The fundamental continuum whose Non-Euclideanism was to investigated was therefore not one of space but of Space-Time, a four-dimensional amalgamation of space and time possessing a four-dimensional metrical field governed by the matter distribution.
-
The final part is the most important part: governed by the matter distribution. That means if we want to know the metrical field you must first know the matter distribution. To be more specific: the matter distribution in time.
That means you need observations in time. That is not easy.
That also raises the question to which extend a concept like density (distribution) can be used. See also page 258
-
-
-
-
Chapter 5.
An alternative View of Non-Euclidean Geometries - page 60
-
-
-
Consider, then, a plane surface.
-
What is the definition of a plane surface?
-
-
-
It is noted that the plane is the same in all three cases, and yet the geometry we obtain on its surface may be Euclidean or non-Euclidian.
-
-
-
-
-
-
-
-
-
Chapter 6.
Time - page 71
-
Our awareness of the passage of time constitutes one of the most fundamental facts of consciousness, and our sensations range themselves automatically in this one-dimensional irreversible temporal series.
-
I will not dispute this. The issue is how scientific and reliable all of this is.
-
-
-
Thus, in the case of time, two sensations A and B may be so close together that it will be impossible for us to determine which of the two was sensed first; yet the same may happen in the case of two sensations B and yet we might have no difficulty in ascertaining that A was prior to C.
-
When I experience two sensations A and B 'at the same time' and the same sensation B and sensation C also 'at the same time' than it does not make sense for me to claim that the sensations A and C 'are not at the same time'
See also page 28
See also Reflection 2 - Sensory continuum.
A more important question is: What is the scientific importance of these human based observations.
-
Now, when discussing space, we saw that the concept of the same point in space, considered at different times, was ambiguous; it was necessary to specify the frame of reference by which space was defined and according to the frame selected an object would continue to occupy the same point or else manifest motion.
-
The concept of motion only becomes manifest if a second point becomes involved.
-
-
-
-
-
-
-
-
-
-
-
-
Page 72
-
The observer who was to pass an opinion on the simultaneity of the two events would then select that particular frame in which he stood at rest.
-
Suppose you have observer A which produces two flashes of light at two moments E1 and E2.
Suppose you have a second observer B which produces also two flashes of light at two moments E3 and E4.
The frame in which observer A is at rest is called frame A. The frame in which observer B is at rest is called frame B. at a certain instant both frames meet (E1 = E3) and then they move away.
The issue is that observer A will always observe the two events E3 and E4 non simultaneous.
The same is true for observer B, with the two events E1 and E2.
Because E1 and E3 are simultaneous (can not be distinguished), most probably the two events E2 and E4 are not simultaneous. The question is: is it possible under certain circumstances that the two events are simultaneous.
-
But from this it would follow that a change in the motion of the observer, hence a change of frame, might bring about a modification in his understanding of simultaneity.
-
The problem is that a single observer can not decide if two events are simultaneous. The flashes (plural) he produces are not simultaneous.
The question to answer is: if it is anyway possible that there are simultaneous events originating a certain distance apart, independent from what any observer thinks?
-
Simultaneity would thus manifest itself as relative, just like position.
-
The simultaneity is always relative and never absolute and then the idea relative does not make sense.
-
As we shall see, Einstein's interpretation of certain refined electromagnetic experiments consists precisely in recognising the relativity of simultaneity and the ambiguity of duration.
-
The ambiguity of duration becomes clear when different moving clocks are involved.
-
-
Page 74
-
-
-
-
-
-
-
-
-
"If an absolute isolated physical system (i.e. one not subject to external influences" reverts once again to exactly the same state as that in which it was at some earlier instant, then the same succession of states will be repeated in time and the whole series of events will constitute a cycle.
-
Important is that the concept in time in mentioned. For example like in the sentence: The whole universe evolves in time.
A second remark is that if we want that a system returns to exactly the same state, implying the same position in physical space then this requires the concept of absoluteness
-
In general such a system is called a clock.
-
For each clock it is important to understand its inner workings
See also: page 74 and page 106
-
Each period of the cycle last equally long"
-
Okay
-
-
-
-
-
-
Page 75
-
We remember that Newton refers to absolute time as "flowing uniformly"
-
As a matter of fact there is nothing wrong with this. The question is if this flowing represents something physical, and this is not the case.
-
But of course this allusion to time does not lead us very far, for a rate of flow can be recognised as uniform only when measured against some other rate of flow taken as standard.
-
The only thing that can be measured is duration.
-
Now both Galileo and Newton recognised as result of clock measurements that: approximately free bodies (moving in an approximately Galilean frame) describe approximately straight lines (with approximately constant speeds).
-
Clock measurements by Newton are performed with a pendulum. With a pendulum only durations can be measured.
The problem is that this is only the case when absolutely no forces are acting on the free moving bodies, which in any real application is never the situation.
-
Newton then elevates this approximate empirical discovery to the position of a rigorous principle, the principle of inertia and states that absolute free bodies will move with absolute constant speeds along perfectly straight lines, hence will cover equal distances in equal times.
-
In equal times is the same as: in equal duration. This is true in theory. Absolute free bodies don't exist. As a result, also absolute accurate clocks also don't exist.
It should be emphasized that the principle of inertia as described, describes a theoretical situation.
-
-
-
It is obvious that, however perfect our measurements, errors of observations will always creep in.
-
Neither measurements nor observations nor the conditions are always 100% correct i.e. ideal.
-
Furthermore, a body moving under ideal conditions of observations can never be contemplated; hence all we can hope to obtain is the greatest possible approximation.
-
The way a body moves, its behaviour, can never be a point of discussion. The issues are the observations and the accuracies
obtained.
-
But although physical measurements become inevitable as soon as we wish to obtain a concrete definition, an objective criterion of equal durations, we are able to proceed in our mechanical deductions in a purely mathematical way without further appeal to experiment.
-
Except, at the end of the exercise new observations or new experiments are required, in order to demonstrate that the results and predictions are correct.
-
The principle of inertia, together with the other fundamental principles of mechanics, enables us, therefore, to place mechanics on a rigorous mathematical basis, and rational mechanics is the result.
-
The issue is not mathematics and its rigour in general, but the mathematics used in every 'special' physical environment.
-
-
-
If peradventure further experiment were to prove that our mathematical deductions in mechanics were not borne out in the world of reality, we should have to modify our initial principles and postulates or else agree that nature was irrational.
-
This last part is nonsense.
At the end of the page:
-
With mechanics, the necessity of modifying the fundamental principles became imperative when it was recognised that the mass of a body was not the constant magnitude we had thought it to be; hence it was experiment that brought about the revolution.
-
The issue of mass is that it belongs to the realm of GR and not to SR. The whole issue that mass is considered a constant is an issue of accuracy or approximation.
-
-
Page 76
-
And now let us revert once again to the problem of time.
-
Okay
-
Theoretically, the law of inertia should permit us to obtain an accurate determination of congruent intervals, but as it was quite impossible to observe freely moving objects owing to frictional resistances as also to the gravitational attraction of the earth and sun, it was advantageous to discover some other physical method of determination.
-
This text indicates how difficult the concept of time is, to be more specific how difficult to define exactly what is an accurate clock. The word interval implies duration.
-
-
-
-
-
-
-
-
Page 77
-
And now let us suppose that we had elected to define time by entirely different methods.
-
Okay.
-
We might, for instance, appeal to the vibrations of some element, such as cadmium
-
Okay.
-
Then the intervals of time marked out by the successive beats of the atom at rest in our Galilean frame would be equal or congruent by definition.
-
This is a very tricky sentence. The issue is not so much if one clock and one atom are considered, but two. The next issue is: it correct to consider only one frame? Does an atomic clock on the surface of the earth beat at the same rate as an atomic clock in intergalactic space? Does it make sense to study the behaviour in a Galilean frame, while generally speaking all clocks are subject of accelerations?
These are all philosophical issues.
-
-
-
-
-
-
Page 79
-
-
-
-
-
And here we may mention a type of objection which is often encountered in people who do not trouble to differentiate between physical time and psychological duration.
-
The issue is how we can predict the evolution of processes in the future based on observations in the past.
If you want to do that, you need some form of accurate universal time keeping. Our senses have nothing to do with this.
-
-
-
The fact that our crude appreciation of time agrees in a more or less approximate way with the more refined methods of scientific determination offers no great mystery, for after all, the laws which govern material processes in the outside world would in all probability also govern that which is material in our organisms.
-
This is a tricky sentence. The issue is that the behaviour of the planets is not governed by certain laws, neither is time, nor the behaviour of organisms. The only thing (?) that is true is that there are similar processes and almost by definition these processes behave similar and are described by similar laws.
-
-
Page 80
-
-
-
We now come to Einstein's definition
-
Okay.
-
As we shall see it does not differ in spirit from the definitions of classical science; its sole advantage is that it entails a minimum of assumptions, and is susceptible of being realised in a concrete way permitting a high degree of accuracy in our measurements.
-
The details of these measurements are very important.
-
Einstein's definition is then as follows: If we consider a ray of light passing through a Galilean frame, its velocity in the frame will be the same regardless of the relative motion of the luminous source and frame, and regardless of the direction of the ray.
-
There are four questions:
- How is the speed of that ray measured from a 'fixed' source to a 'fixed' destination over a 'fixed' distance?
- Will this be the same in all directions?
- Will this be the same in every Galilean frame?
What has a frame to do with this?
-
It follows that a definition of equal durations in the frame will be given by measuring equal spatial stretches along the path of the ray and asserting that the wave front will describe these equal stretches in equal times.
-
The problem with this sentence can best be described by the following example:
- Consider a rigid rod in a Galilean frame. The two ends are called F (Front) and B (Back).
At moment t0 there is a flash of light at point B. This flash reaches point F at t1.
- Consider an identical second rigid rod in a different Galilean frame with a speed vx.
At moment t0 the two points B of both rods meet each other. The flash also reaches point F of the second rod at t1.
When that is the case the speed of light in both Galilean frames is now the same.
But is this physical correct? IMO not based on what is observed in either frame. In neither frame
the light flash can hit the points F simultaneous. That means in neither frame the duration of the light flash (From B to F) for each rod can be the same.
-
-
Page 81
-
And how can we ascertain the equality of a velocity in all directions when we do not yet know how to measure time?
-
The only way to ascertain the equality of a velocity in all directions is first to define an experiment which establishes that the speed of light is the same in two opposite directions. Of course if you cannot demonstrate this without a clock you have a problem.
-
Consider a circle along which two bodies are moving in opposite directions.
-
This is a circle or a track on the surface on the earth
Okay.
-
We shall assume that the two bodies leave a point A at the same instant (tS) of time, hence in coincidence, and then meet again (tE) at a point B halfway round the circle, hence diametrically opposite A.
-
The instant (tS) is not a coincidence. The initial starting position and condition of the experiment is selected on purpose.
The instant (tE) is also not a coincidence. The experiments involves that body (1) travels from A to B via C and that body (2) travels from A to B via D.
Suppose that body (1) arrives the first at point B. Instant (tE) is now defined when body (2) arrives at point B. The average speed is the length of curve ACB divided by (tE-tS).
There is equal chance that body (1) arrives first at point B or that body (2) arrives first at point B.
The chance that body (1) and body (2) arrive simultaneous at point B = zero
-
But these spatial routes are of equal length; hence we must assume that the speeds of the bodies along their respective paths have been the same.
-
This is only true for their average speed, calculated based on the condition when both bodies have reached point B.
-
In all rigour, we may only claim that the mean speed has been the same, since one body may have slowed down and then spurted on again, making up for lost time.
-
We may only claim that the mean speed has been the same after both bodies have reached point B. We may not claim 'anything' about the actual speed going from A to B by body (1) and body (2).
-
-
-
-
-
-
-
But if we repeat the experiment with circles of different sizes, and if in every case the bodies meet one another at the opposite point, we are justified in asserting that not only the mean speed , but also the instantaneous speed at every instant, is the same for either body.
-
In this experiment, in each trial, the average speed of both trains is always the same, but also different in each trial.
This does not say anything about the instantaneous speeds during each trial.
-
In short, thanks to spatial measurements coupled with the observation of coincidences, we have been able to establish the equality of two velocities, even though we knew nothing of time-measurement.
-
In this experiment we can only say some thing about the average speed in each experiment, but nothing about the average speed between different experiments.
-
A more elaborate presentation of the same problem would be given as follows: Waves of light leaving the centre of a sphere simultaneously are found to return to the centre also in coincidence, after having suffered a reflection against the highly polished inner surface of the sphere.
-
If a short pulse of light emitted at one instance at the centre of a sphere, also is received simultaneous at one instant than that would have been a coincidence.
The problem is that that is not as simple as it sees. To get an idea select: The operation of a Clock in a Centrifuge
In this document the first the behaviour of two types clocks are discussed and secondly a clock in a linear accelerator and a centrifuge are compared. The inner workings of the clock studied, is based on light signals.
Assume that a clock moves towards the right. The behaviour of two clocks is different if in one clock the internal light signals inside the clock move forward and backward in the same direction of movement versus a clock in which the internal light signals move perpendicular to the direction of movement. In the second case the mathematics involved is accordingly to the Lorentz transformations. In the first case: this is not.
In general what this text indicates that when you transmit a light signal in two opposite directions, from the centre, between two mirrors at the same distance each from the center, than the reflections will be received simultaneous. The issue is that reflections between different directions will not be received simultaneous.
-
-
The next sentence continuous at page 82
-
As in the previous example, the light waves have thus covered equal distances in the same time; whence we conclude that their speed is the same in all directions.
-
That is only true if you assume that the origin of the reference system used is at rest. This is generally speaking never the case. In such a special frame the duration of a flash of light travelled in equal directions in both directions is the same.
In normal circumstances, that is not the case and all sorts of complications arise. See above where the centrifuge is discussed.
-
-
-
-
-
-
-
-
Page 82
-
Inasmuch as this experiment has been performed, yielding the results we have just described, even though the ether drift caused by the earth's motion should have varied in direction and intensity, the isotropy of space to luminous propagations was thus established (The experiment described constitutes but a schematic form of Michelson's).
-
In the previous discussed example, at page 81, the issue is light waves. In the case of the Michelson and Morley experiment these waves are observed by means of interference patterns.
In the case of clocks the oscillations are light pulses. No interference patterns are involved.
-
-
-
-
-
-
-
Now, the importance of Einstein's definition lays not so much in its allowing us to obtain an accurate definition of time in our Galilean frame as in its enabling us to co-ordinate time reckonings in various Galilean frames in relative motion.
-
The physical problem is that all clocks with different constant speeds show different time readings.
-
-
-
-
-
-
-
-
Chapter 7.
Systems of Co-ordinates and Distance - page 83
-
-
-
An alternative presentation of non-Euclideanism (in the case of two-dimensional geometry) was than found to be afforded by assuming that the distance between the points could in all cases be determined by measurements with rigid Euclidean rods; but that whereas in the case of Euclidean geometry all the points should be considered as existing in the same plane, in the case of non-Euclidean geometry it would be as though the points were situated on a suitable curved surface.
-
A physical curved surface of what? The surface of an apple? The surface of the earth?
This is very important because the surface of the earth is a 3D object.
The trajectory of a comet is globally bended, but physical an ellipse in 3D.
The trajectory of a flash of light (emitted by a star) is globally bended around a star, from our point view, but physical this flash is a sphere, distorted by all interfering objects, small and large.
See also page 287
-
-
-
Thus in the case of the Earth, the non-Euclidean distance between two points, say New York and Paris, would be given by the Euclidean length of great circle extending between these points, hence by a curved line following the contour of earth's surface.
-
Correct.
For astronomical physical applications only the Euclidean distance (i.e. the straight line) is important.
-
-
-
-
-
-
-
-
Page 84
-
In this way every point of intersection is defined by two numbers, and these numbers are called the Cartesian co-ordinates of the point
-
Okay.
-
-
-
Hence once again we see that it is only relative to the co-ordinate system that points can be defined.
-
That is correct.
If you want to define positions, you always need a coordinate system.
The word relative, as such, has no meaning.
-
-
-
It would be feasible, in place of our horizontals and verticals, two select two families of intersecting curves, which we might call the u and v curves.
-
Generally speaking to use such curves compared to straight lines is mathematical speaking much more complex.
At the end of page 84 we read:
-
The necessity of generalising Cartesian co-ordinates by introducing Gaussian ones arises from the fact that Cartesian mesh-systems of equal squares can be traced only on a plane and never be drawn on a curved surface, like that of a sphere, for example.
-
What about the formula to define a sphere: x^2 + y^2 + z^2 = R^2?
See also: page 262
Page 85
-
Hence, were we to ignore the use of Gaussian mesh-systems, it would be impossible for us to localise points on a curved surface, by means of a mesh-system applied on the surface.
-
To localise points on any surface you need a mathematical description, or a set of functions to describe the surface.
-
-
-
-
-
-
-
-
-
-
Page 86
-
-
-
In short, the distance DeltaS between P and Q cannot be fully determined by DeltaU.
-
Correct.
-
It is customary to designate A by Sqrt(g11) so that, using squares, our formula becomes ds^2 = g11 * du^2
-
Correct.
-
Inasmuch as the distance ds between these point pairs varies from pole to equator, we see from ds^2 = g11 * du^2 that g1 must vary in an appropriate way as we consider various portions of the sphere's surface
-
It is here to point out how complex the introduction of the concept of g11's is, related to curved surfaces in general; they are every where different i.e. point specific.
-
-
-
-
Page 87
-
Hence we must conclude that even at a fixed point of our surface the value of g11 will be subject to change when we vary our mesh-system.
-
Point taken.
-
-
-
-
-
-
-
-
-
-
Page 89
-
-
-
-
-
In other words, we have
-
g11 = I; g12= 0; g22=u^2.
This proves once again that the values of the g's vary with our choice of a co-ordinate system.
-
This does not prove something. This is much more a determination.
-
-
-
-
-
-
Page 90
-
-
-
(3) The value of the square of the distance between two infinitesimally distant points is given by
-
ds^2 = g11*du^2 + 2*g12*dudv + g22*dv^2
Where the values of the g's and of du and dv will vary when the mesh-system is changed or when we consider different regions of the same mesh-system.
-
This is 100% correct. This is also an important issue, raising all practical limitations.
-
The only case in which the g's will remain constant is when the mesh-system is of the uniform type, that is, a network of two families of parallel lines intersecting one another
-
That is the case when the distance du and dv are constant throughout the mesh-system.
-
-
-
It is a remarkable fact that although everything entering into the expression of ds^2 varies when we change our mesh-system, yet the value of ds^2 as defining the value of the square of the distance between two infinitesimally distant points remains unchanged.
-
This is what you should expect, because every length of a physical object or a box should be independent about the reference system used. If you use the same methodology to define a distance between two fixed locations the result also follows the same logic. See also page 83
-
In other words, ds^2 is a scalar an invariant.
-
Any distance is always a scalar.
The same with ds^2 = dx^2 + dy^2 + dz^2
However if you know the distance between two points you don't know the position of each point.
See also: page 195
-
-
-
-
Page 92
-
-
-
All this goes to prove that the curvature of a surface must exert a modifying influence on the g distribution, since when the surface is curved no constant distribution is possible.
-
You cannot call this: a proof. The issue is when you start with a flat surface there must be a physical influence which causes the flat surface change into a curved surface.
At the same, and this is important, when modifying influence changes (i.e. the distribution of matter) the g distribution also changes.
-
We must infer, therefore, that the g distribution is governed by two separate influences: first by the intrinsic curvature of the surface from place to place; and secondly by our choice of mesh-system over the surface.
-
Both the wordings governed and influences are wrong. Both words implicate something physical, but this is not the case.
The only thing that is physical is the cause of the curvatures. See above.
-
Obviously, if it were possible to discover some mathematical expression connecting the g's at one point with the g's at neighbouring points, and if this mathematical expression remained invariant in value to a change of mesh-system in spite of the variations of the individual g's which must accompany the change of the mesh-system, we should be in the presence of a magnitude which, would refer solely to the shape of the surface itself, i.e., to its curvature at the point considered.
-
It is much more important to have a mathematical expression for the modifying influences on the curvature i.e. on the g distribution.
-
-
-
-
Page 93
-
The curvature of the curve A is defined by the curvature of its osculating circle at A. Calling R the radius of this osculating circle, the curvature of the curve at A is thus given by 1/R (Fig VI)
-
Okay.
-
-
-
-
-
-
-
-
-
-
Page 95
-
-
-
-
-
In a general way, therefore we may state that the type of geometry of our two-dimensional space from place to place is defined by the value of the Gaussian curvature from point to point, hence by the law of g-distribution throughout space; and that when space is Euclidean, the g-distribution is always such that the Gaussian curvature vanishes at all points, regardless of the particular mesh-system selected.
-
It should be mentioned that the curvature of a surface in principle says something about three-dimensional space and not two-dimensional. The critical point is what means 'space'
-
-
-
-
-
-
Page 96
-
As for the invariant mathematical expression of the square of a distance, between two points, it now contains a greater number of terms.
-
Okay.
-
In the case of three-dimensional space we have no longer three separate g quantities at every point; this number is increased to six.
-
Okay.
-
In the case of a four-dimensional space it is increased to ten, and in the case of an n-dimensional space to n*(n+1)/2
-
In this case we should speak about mathematical space.
-
-
-
-
-
-
-
-
-
Owing to the importance of a four-dimensional extension in the theory of relativity, we shall write out the expression of the square of the distance for a four-dimensional space.
-
This becomes part of mathematical space.
-
Proceeding by the same method as we did in the case of two dimensions we may construct, as before, an invariant relation between the gik's at any point of the continuum and their values at neighbouring points; the invariance of this relation implies that its magnitude remains unchanged when the mesh-system is altered, and so this magnitude defines some intrinsic property of space itself.
-
The question arises how are these gik's calculated in reality and how many sets are required.
The fact that "its magnitude remains unchanged" is of little practical value, because they have to be calculated at least once.
Compared to Newton's Law, also all the masses (of the planets) of our solar have to be calculated at least once, based on observations. The fact that, some else can do the same, using a different co-ordinate system and will come up with the same result, is of no much practical value. It improves confidence.
See also page 199
-
The invariant magnitude here considered is the generalization of the Gaussian curvature G of surfaces, extended to four dimensions.
-
It should be remembered that the curvature of a (two-dimensional) surface is physical the curvature of a three-dimensional object.
From a mathematical point of view the curvature of geometry in three dimensions reflects geometry in four dimensions or in four-dimensional mathematical space.
Physical such geometry does not exist.
-
We shall represent it by the same letter G
-
Okay.
-
Except for the more generalized form of the Gaussian curvature, the situation seems to be much the same as the two-dimensional surface.
-
A three-dimensional surface raises a physical problem.
-
But a novel feature arises when we wish to determine the geometry of space.
-
Let us wait and see. The word space is tricky.
-
Thus we recall that in the case of a two-dimensional surface, the invariant of curvature G (or Gaussian curvature) fully defines the geometry of space.
-
What is defined is the surface of a three-dimensional object.
-
For instance, if the Gaussian curvature vanishes throughout, the surface is Euclidean or at least flat.
-
The surface of the 3D object is flat.
-
-
Page 97
-
But when we consider spaces of more than two dimensions, knowledge of the generalised Gaussian curvature throughout the space is no longer sufficient to fix its geometry.
-
Is this mathematics or physics?
This is a very important question. In the physical world everything that exists is three-dimensional.
This remembers me about the problem: how does a frog proves that the world is 3 dimensional, when from his point of view the world is flat or 2D.
-
Consider our Earth and that there is a frog, which lives on the North Pole.
First he travels a small distance in any direction. He makes right turn and travels the same distance. He does the same again and again and he realises that he is back from where he started.
He repeats this same experiment with the only difference that he travels towards the equator. He makes right turn and travels the same distance. Next he does the same again and he realises after three turns that he is back from where he started. In the first experiment this was four turns. What is the explanation?
Now the frog starts thinking and thinking and then he speaks the clever words: The world on which I live is not flat but curved. I live on a 3D sphere. A clever frog.
|
-
There still remains a large measure of indeterminateness in the actual geometry of the space.
-
Finally the actual geometry of space has to be calculated based on observations.
-
Fortunately, for spaces of more than two dimensions, another magnitude serving to define the geometry of the space is at our disposal.
-
Why bother. As I mentioned before there is a clear distinction between mathematical space and physical space.
See: Reflection 7 - Physical space versus Mathematical space.
-
-
-
-
-
-
-
-
-
-
-
-
-
In the case of four-dimensional space there are 256 of these components, but as some of the components always vanish and others are repetitions, we are left with only 20 independent components.
-
Still a lot to be calculated based on actual observations.
-
If in any given mesh-system the values of the 20 components of the Riemann tensor are known at each point of the space, the geometry of space is completely determined.
-
Implying from here to eternity? I doubt that.
This space is mathematical space in which one dimension is time. That means accuracy is an issue.
-
-
Chapter 8.
The Meaning of the word Relativity - page 99
-
In traditional philosophy an absolute reality is the primary, self-existing reality, the substance, the true being or the metaphysical reality whereas a relative reality is a secondary, dependent reality owing its form of being to a relation of the genuinely real.
-
IMO there exist only one reality which is the whole universe in all it finest details.
All paintings are part of this reality. The problem starts if you want to compare different paintings. You can call some better as others. When you do that, you introduce a form of relativity.
-
Now, so far as scientific philosophy is concerned, absolute reality is a myth.
-
This requires the definition of the concept 'absolute reality', before to call it a myth.
If it is a myth the word absolute should be skipped altogether.
-
Obviously, then, when physicists speak of absolutes and relatives, they are referring to categories of nature differing from those of philosophers.
-
No. This is not obvious. It should be the physicists, with the aid of philosophers of science, who should set up the rules how to perform physics. One of these rules should be that if two related concepts are used both require a clear definition.
-
We have seen, when discussing mathematical space, that according to our measuring standards, which were conventional, these length might be equal or unequal; and it was this aspect of relativity which expressed the fundamental mathematical relativity of length.
-
See also page 30 and page 47
-
-
-
We saw further that bodies which were thereby defined as congruent constituted what are known as Euclidean solids, and that these were assumed to remain absolute in length, regardless of the observer's motion.
-
An object can only change (For example: in length) as a result of a physical process i.e. an action. The motion of an observer (itself) can not cause (generally speaking) any physical change. This is demonstrated when the observer returns to his original location. The only (?) exception is when the observer has a clock.
-
-
Page 100
-
-
-
-
-
-
-
Consider a telegraph pole rising vertical from the ground. The visual angle under which this pole will appear to us is essentially relative, since it varies in value with the distance of the observer from the pole.
-
This is typical an issue related to observations i.e. the observer and can not be considered a law of physics. There are no physical changes involved.
-
Of course this visual angle is fundamentally relative, since its value depends on the system of geometry we adopt, but we are no longer discussing this mathematically aspect of relativity.
-
This is typical not a physical aspect.
Next paragraph
-
In contradistinction to the relativity of the visual angle, classical science considered that the length of the pole itself was absolute, being irrelevant to our relative position as observers.
-
Science in general only is involved with physical phenomena i.e. changes.
A different position of an observer does not involve any physical change of the studied process.
-
Once again, if we argue as mathematicians, we may claim that this length in turn is relative, since it depends on our measuring conventions.
-
The whole issue is if something physical changes. This is not the case.
-
-
-
Such being the case, classical science believed that the length of the pole was an absolute, in as much as its numerical value was so many feet or so many metres regardless of our position and regardless of our motion.
-
That is correct, except that classical science (Newton) does not use the word absolute in this sense.
(IMO he uses the word absolute for the total universe...)
-
The absolute magnitude is not the length of the pole; for this, analogously to visual angle, is relative.
-
The use/meaning of the wording absolute magnitude is not clear.
To compare the length of the pole with the visual angle is tricky.
Generally speaking the physical length of a pole will only change when there are physical actions involved which try to shorten the physical length of the pole. Such a process is always asymmetrical because the result cannot be undone.
The observed length will change and the visual angle will change when the position of the observer changes, but this is not a physical effect.
-
The absolute magnitude is rather a something with transcends space and time, and relates to the absolute world of space-time
-
What this implies is that space-time is not something physical but mathematical. It is calculated. To call it absolute is tricky.
-
A second illustration may be given by the concepts of mass and weight.
As a result of result of Newton's discoveries, the weight of a body was realised to be relative, since its value varied with the proximity and distribution of matter.
-
The weight of a body is typical a calculated quantity, but so is mass.
See Reflection 8 - Newton's Law and the movement of the planets.
The weight of a body is a force. The forces involved are a function of the distribution of matter.
-
On the earth's surface the value was many tons, on the surface of the moon it was considerably reduced and in stellar space it completely vanished.
-
The forces between (collection of) objects never vanish completely.
-
A body of itself had no weight.
-
To consider a body at itself is irrelevant.
-
In contradistinction to the relativity of weight, classical science assumed that mass was absolute.
-
Classical science does not assume that mass is absolute. Mass in stellar applications is considered (once calculated) a constant in time. Weight, velocity and accelerations are not.
-
The mass of a body, wherever situated and in whatever circumstances observed, was supposed to be an invariant remaining always the same.
-
As mentioned above mass is a calculated value based on observations, in time, on the distribution of surrounding matter. In first approximation all objects considered are considered point masses. If the shape of any object changes this should be included in the calculations, because this can influence the behaviour of the objects directly involved, including all the other objects considered.
-
For this reason, mass, in contrast to weight was assumed to be immanent in matter. It was not the result of a physical relationship, but was a reflection of the very existence of matter.
-
This is nice prose...
The problem is that mass is a physical calculated parameter (based on observations in time) of an object based on the physical forces between objects.
-
-
-
-
-
-
-
-
Page 101
-
-
-
-
-
The preceding examples teach us two things: First of all, it is not sufficient to state that a concept is a relative; we must complete our statement by stipulating with respect to what surrounding conditions this concept happens to be relative: whether it e.g. to the distance of the observer, to his motion or to the distribution of matter.
-
The evolution of physical processes has generally speaking nothing to do with human activities. As such, the position of neither the observer, nor his motion has anything to do with the laws of nature. Of course when the position of an observer changes (in time) what he sees or observes changes. This becomes worse if both the observer and the object he observes changes as observed by a second observer.
Observing the distribution of matter (in time) is something complete different. The evolution and the movement of stars are physical processes in which real changes can take place.
This is also true for the behaviour of a clock, which inner workings is based on light signals.
-
-
-
-
-
-
-
-
-
-
-
In classical science it was always assumed, that a distance in space, duration in time and simultaneity between distant events were absolute concepts.
-
In classical science the word absolute is almost never mentioned and is of almost no use. A distance is the distance between the positions of two points. Duration is the time between two clock readings.
In classical science starting point is one reference frame.
-
Regardless of the relative motion or position of the observer, regardless of the distribution of matter, these concepts remained unchanged.
-
Generally speaking the velocity and position of an observer have no physical effect of what is observed.
-
-
-
Einstein succeeded in proving that these opinions must be erroneous, since they were incompatible with certain refined optical experiments.
-
The understanding of this sentence lies in the details of the experiments involved.
-
He showed that the relative motion of the observer could not help but exert a modifying influence
-
Generally speaking observers have no influence on the studied processes (in space). That does not mean that the observer can not influence what is observed. In many cases observations (the place and the time) are observer dependent, implying that what the observer observes/sees can change over a period of time, but not the processes observed.
Anyway more detail is required.
At the end of the page we read:
-
Henceforth, distance, duration and simultaneity become relative expressing relationships between the magnitudes measured and the relative motion of the observer.
-
It is the objective of science to develop laws, describing the evolution of the universe, independent of any observer.
Of course different observers can observe the same events differently. In reality these different observations have no physical influences and should be eliminated from what is observed.
Page 102
-
Just as the visual angle under which an object appeared to an observer was in no wise immanent in the object itself, since it varied with the observer's position, so now length, duration and simultaneity are in no wise immanent in the real world, since they vary with the observer's motion.
-
In general when an observer is in motion his observations will change compared with an observer which is at rest in the same frame.
However this has no physical consequences.
-
Once more we must draw attention to the fact that the relativity we are discussing is essential physical; it is posterior to our definitions of practical congruence.
-
What is meant with: essential physical?
-
-
-
They are not merely conceptual; they are perceptual.
-
Of course everything that is perceptual also causes some physical changes, but these are physical changes in the brain of the observer him or herself, but not necessarily physical in the processes under consideration.
-
-
-
The major aim of the theory will be to separate those magnitudes which are relative from those which are absolute (are unaffected by this motion)
-
See also Reflection 4 - Absolute versus relative in Newton (Classical) versus Einstein.
-
The absolute magnitudes will then be representative of the absolute common world of which the various observers will obtain but private perspectives.
-
The emphasis should be towards the physical world.
-
This absolute world will be the world of space-time standing in contrast to the relative world of space and time.
-
There exists no physical world of space and time. What exists is a physical world in time. The biggest problem is time because clocks are not accurate. They are a function of their own behaviour i.e. speed.
-
-
Chapter 9.
The Principles of Relativity - page 103
-
-
-
Let us consider these various principles in their order. (1) The mathematical type of relativity is the one we have already had occasion to mention when discussing mathematical space and time.
-
Okay.
-
-
-
-
-
(2) The kinematical or visual principle of relativity, which is at least as old as the Greeks, states that a body can be considered in motion when referred to some other body.
-
Did the Greeks mention the word relativity? The word motion requires a clear definition of what means motion versus what means not in motion. Specific not in motion is the most difficult. Of course you can declare yourself within your own frame at rest, but everyone can do the same and that does solve the issue.
The first step is to agree upon the idea that there can only be one frame to be called at rest. Within that frame all the physical objects considered can be in motion, because change is something inherent in this world.
At the same time it is possible to define a virtual grid in this frame, with virtual clocks which all run synchronic and which are all at rest.
See also: page 16 and 17
See also: Reflection 4 - Absolute versus relative in Newton (Classical) versus Einstein.
-
-
Page 104
-
(3)The Newtonian or Galilean or classical or dynamical principle of relativity expresses this elusiveness velocity or Galilean motion through space so far as mechanical experiments are concerned, while it stresses by contrast the physical significance of absolute acceleration and rotation.
-
Both the concept absolute velocity and relative velocity are not clear in the sense that there is no ambiguous definition.
To call acceleration absolute is also highly questionable, because its direction and absolute value (its length) constantly changes when objects move through space in time, as influenced by all the other objects considered.
-
-
-
-
-
We now come to (4) Einstein's special principle of relativity. It is an exact replica of the Newtonian principle, upholding the relativity of velocity and the absoluteness of acceleration.
-
The Newtonian principle is more than that.
-
-
-
-
-
-
-
There, we are introduced to the (5) General Principle of Relativity.
-
Okay.
The last sentence: (partly at page 104 and 105)
-
The principle states that the mathematical expressions of the laws of nature must maintain the same form regardless of our choice of a frame of reference, be it Galilean (i.e., not accelerated through empty space) accelerated or even squirming like an octopus, while our clocks situated throughout the frame may beat at the most capricious rates.
-
The principle states in short, that the laws of nature are completely independent from any reference frame. In fact the principle claims that the evolution of all the physical processes in nature should be independent of any reference frame. That seems logical because a reference frame is something mathematical.
The problem with a clock is: that a clock which internal working is based on (reflection of) light signals does not operate properly i.e. accurately.
The question is: Why consider an accelerated frame of reference in the first place?
See Reflection 8 - Newton's Law and the movement of the planets.. This reflection shows then when different frames are used as part of the observations, to perform your simulation you have to adapt the transformation equations.
See also: page 266
-
-
Page 105
-
-
-
The general principle of relativity, by extending the invariance of the laws of nature to all types of motions of the frame of reference, marks the starting point for the possible relativisation of acceleration, which had heretofore stood aloof and as distinctly absolute.
-
See also Reflection 6 - Frames.
In short: the general principle of relativity states that the laws of nature are independent of any reference frame including acceleration.
-
The radical (6) Mach-Einstein principle of relativity is the result of a natural desire to bring about the complete relativisation of all manner of motion, rotationary and accelerated, as well as uniform.
-
The problem when you call everything relativistic, the word relative looses its physical value.
-
This is achieved etc to motion with respect to the material universe as a whole.
-
Such a global approach is preferred.
-
According to this principle, which is still highly speculative, there can exist no observable difference between the rotation of a body with respect to the universe of stars and the rotation of stars round the body; exactly the same dynamical effects of centrifugal force would be set up in either case, so that no trace of absolute motion through empty space would be left.
-
This principle can only be studied if three objects are considered: One object representing all the masses and stars in the universe and two binary bodies. From the point of view of each of the two binary bodies all the stars are moving. From the point of view of the universe only the binary bodies are moving. That means there is a physical difference: The whole universe can be considered at rest, while individual objects are moving.
-
-
-
-
Chapter 10.
Classical Mechanics and the Newtonian Principle of Relativity - page 106
-
-
-
The measurement of the velocity of the body with respect to our frame necessitates the addition of a clock.
-
Correct.
The issue is: What is this speed versus the speed of light.
-
We will assume that this clock beats out congruent intervals of time, where congruence is, of course defined by the requirements of practical congruence for time, that is, by the beats of some isolated periodic mechanism.
-
We assume here that the inner working of the clock is based on light signals.
See also: page 74
-
-
-
Again, if a stone is allowed to fall from a great height, its motion with respect to the earth will be accelerated, whereas, with respect to a frame of reference falling together with the stone, it will have remained at rest.
-
While the floor approaches the stone with acceleration.
-
-
Page 107
-
-
-
In other frames no such forces were apparent (excluding the force of gravitation), and space appeared stagnant and quit, the same everywhere.
-
This is only in theory possible. Specific the force of gravitation is always available.
-
These latter frames are called Galilean or Inertial.
-
The whole point is that nowhere in the Universe any object can move in a straight line with a constant speed. Except is the universe is empty. This becomes clear when three objects are considered, with the studied object somewhere in between the other two.
-
-
-
Mechanical experiments conducted in the non-Galilean frames proved that the disposition of the strange unsymmetrical so-called inertial forces bore a close relationship with the apparent motions of these frames as viewed from the Galilean ones.
-
Okay.
-
-
-
In a non-Galilean frame rotating with respect to a Galilean Observer, the disposition of the inertial forces would be much more complicated.
Okay
-
-
There would be the centrifugal force pulling outwards and the so-called Coriolis forces pulling sideways.
-
Okay.
-
-
-
-
-
-
-
In short, all the simple laws observed from Galilean frames would have to be compounded with the effects of these strange inertial forces when we wished to formulate laws controlling phenomena as viewed from the non-Galilean frames.
-
The law that describes a rotating object, viewed from a Galilean frame, is complex. For example each planet around the Sun is also a rotating object. When the planet itself is also rotating, to take that into account, becomes even more complex.
-
-
-
-
-
-
-
-
Page 108
-
It follows from the law of inertia, according to which free bodies, when viewed from Galilean frames, will describe straight lines with constant speeds
-
In our Galaxy there are no free bodies, which move in straight lines with constant speeds.
Next is written:
-
That the stars, being presumable free bodies, will obey this law (of inertia) and, owing to their remoteness, appear to suffer very slight displacements even in the course of a century.
-
As mentioned again: In our Galaxy there are no free bodies.
The stars in our Galaxy don't follow straight lines.
-
-
-
This fact led to a more easily obtainable definition of a Galilean or inertial frame, namely, a frame with respect to which the stars would appear fixed.
-
When you take our Galaxy as a whole there are no stars which are fixed. The only exception is the Black Hole in the center. This Black Hole is the preferred origin of a Galilean frame to study the behaviour of stars over a long period.
A frame centred on the Sun can be used to study the behaviour of the planets. In that frame the stars can be considered fixed, but only for a small period.
-
Its sole advantage is that it leads to a more accurate empirical determination of a Galilean frame and shows us immediately that our earth does not constitute such a frame, since the stars appear to circle round the Pole star.
-
The fact that there is one special star i.e. the Pole star, which position is "fixed", implies that something else is at stake i.e. the rotation from the earth around its own axis (in twenty 24 hours).
When you don't take into account the next reason why our Earth is not a Galilean frame is because it rotates around the Sun.
-
-
The next sentence over lapses both page 108 and 109.
-
The problem to determine is, "Why do different types of frames exist why our understanding of amorphous mathematical space would seem to preclude any such difference"
-
The problem is that you can not compare the two types of frames discussed i.e. Galilean frames versus non Galilean frames with mathematical space, because the first two are physical concepts and mathematical space is not.
What makes this even more difficult that in reality all frames are non Galilean because Galilean or inertial frames are simplifications.
-
If we follow Newton we must assume that the peculiarities existing in our frames are not to be attributed to causes existing beyond them
-
Newton's world, generally speaking was the solar system.
-
-
-
A number of philosophers attacked the Newtonian hypothesis of absolute motion and absolute space.
-
The problem is you can easily make this claim now, in 2019. As said above Newton only used one reference frame: the Sun.
In such a frame to use the word absolute does not make sense, specific related to observations i.e. space.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Page 109
-
-
-
-
-
Newton thus objectivises space, and, owing to the symmetrical conditions which endure in Galilean frames, assumes these latter to be at rest in space (or in uniform rectilinear rotation), whereas the non-Galilean frames are assumed to be accelerated or rotating.
-
It should be remembered the only frame Newton discussed (in detail) was the Solar system.
In respect with the universe this is a non-Galilean frame because it is rotating in our Galaxy.
See also: Reflection 6 - Frames.
-
Galilean frames are those which are non-accelerated; non Galilean ones are those which are accelerated or rotating in this absolute space.
-
Better: In the Universe.
-
This was Newton's solution, and provided we accept his postulate of isolation there appears to be no way of escaping it.
-
The whole question is: is Newton's solution correct.
The strategy of Newton was: he studied the solar system in isolation, in the universe.
Page 110
-
-
-
-
-
-
-
-
-
-
Page 111
-
-
-
-
-
-
-
-
-
-
-
But, still more important, it appeared impossible for classical science to account for these dynamical actions attributed to the stars.
-
The word appeared is wrong. The only thing that modern science can do is to give a better explanation than classical science.
-
-
Page 112
-
-
-
The Principle of Relativity of Classical Science merely summarises these discoveries by stating that it is impossible for an observer situated in a Galilean frame to ascertain by any mechanical experiment whether he is at rest in space or in a state of uniform translationary motion.
-
- What are discoveries?
- How does any observer know that he is in a Galilean frame?
- If a person can not by any experiment demonstrate that he is at rest than he should assume that he is in motion.
See also page 17
-
We see, then, that acceleration has an existence per se and that, in contrast to velocity, it is determinate even in the absence of a frame of reference.
-
Here the definition of the word determinate is very important.
The problem is that for any physical process (to evolve) a reference frame is not important. A reference frame becomes important if you want to quantify what is observed. At the same time a reference frame is not useful in empty space.
-
-
-
-
-
-
-
-
Page 114
-
-
-
-
-
Accordingly we are led to Einstein's special principle of Relativity, which states that not only mechanically, but in every way, absolute velocity through space must escape empirical detection.
-
The concepts relative versus absolute velocity only makes sense when there is a clear difference, in the definition, between both. More important is, how velocity exactly is calculated.
-
-
-
-
-
-
Chapter 11.
The Ether - page 116
-
Classical science assumed that those manifestations we called electricity, magnetism, and light were nothing but strains, compressions and wave like motions in an imponderable medium, the stagnant ether, floating in space.
-
The whole issue is: is there something what we can call empty space. The fact that we in certain regions of space we (humans) can not observe anything does not mean that space is empty.
In reality the whole of space is filled with photons. So the universe is never completely empty.
Along the same line it is difficult to define a vacuum as being a state somewhere in the universe.
-
-
-
At any rate, once the existence of semi-material ether was accepted it was natural to suppose that the motion of our optical and electrical apparatus through its substance should exert a perceptible influence on the results of experiment.
-
This depends on what this ether is.
A moving clock, which working is based on light signals, behaves different compared with a clock at rest. The clock at rest runs the fastest.
-
-
Page 117
-
-
-
-
-
But the entire trend of recent research had been to show that this distinction was unjustified.
-
This sentence requires much more detail.
-
-
-
-
-
It is true that Michelson's very refined test attempted in 1887 failed to detect any influence of absolute Galilean motion in a certain optical experiment; but it was always assumed that an explanation for this failure would be fortcoming sooner or later, and that other experiments would be successful where Michelson's had failed.
-
Under Construction
-
-
-
-
Page 118
-
-
-
This operation is called a mathematical transformation; and the equation operated upon is said to have been transformed.
-
Okay.
-
In the type of problem we are considering, when one frame of reference is replaced by another, the transformation will bear on the space and time variables or co-ordinates present in the equation; and transformations of this character are termed space and time transformations.
-
In this sentence the wording "space and time" is correct. It reflects mathematics.
-
-
-
-
Page 119
-
-
-
-
-
These space and time transformations permitting us to pass from one Galilean frame to another were the celebrated Galilean transformations of classical science, and they were, as we have seen, the necessary consequences of our belief in absolute duration and distance.
-
Again it is here important to have and ambiguous definition of the difference between absolute versus relative.
See also: Reflection 4 - Absolute versus relative in Newton (Classical) versus Einstein.
-
-
-
-
-
-
Page 123
-
-
-
-
-
-
-
-
-
This required percentage of drag of the ether by dielectrics was called Fresnel's convection coefficient
-
Okay
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Chapter 12.
The Equations of Electromagnetics and Lorentz's Theory - page 125
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Page 127
-
-
-
-
-
-
-
Precise measurements conducted on electrified bodies and magnets then proved that the value of this ratio was about 186,000 miles per second; whence it became necessary to assume that periodic perturbations in the strains and stresses of the field would be propagated in the form of waves moving through the ether with this particular speed.
-
The words strains and stresses require an explanation.
-
But this velocity was precisely that of light waves propagated through the ether.
-
This was the starting point of the principle or the postulate of the invariant velocity of light. See also page 147
-
-
Page 132
-
Now, the Michelson and Morley experiment is precisely of this type
-
Okay.
-
It is assumed that the reader is sufficiently familiar with it to render its detailed description unnecessary.
-
That is very unfortunate because a detailed description is very useful. See next sentence.
-
Stated briefly, the experiment proves that if waves of light leave the centre of the sphere simultaneously, they will return in perfect unison to the centre of the sphere after having been reflected against the sphere's inner surface, no matter in what direction through the ether, or with what constant velocity, the sphere attached to the earth may be moving.
-
First of all it should be mentioned that this experiment is conducted in the plane on the surface of the earth.
The way the experiment should be set up is that you start with a perfectly round large mirror, in the form of a ring. At the centre is a light source, which emits a light flash. This flash of light propagates in the form of a ring, is reflected by the mirrors and moves backwards to the focus point of the mirror. The result should be, that all the individual small sections of the flash, should meet simultaneous at the focus of the sphere.
The MM experiment does not use this setup. In that experiment the light source does not emit a flash, but a flash of certain duration and what is measured as an interference pattern.
-
-
-
Page 134
-
-
-
-
-
-
-
-
-
-
At the bottom of page 134:
-
Accordingly, he laid down his celebrated principle of correlation, according to which adjustments were so regulated in nature that the velocity of our planet through the ether could never be detected, however precise our experiments.
-
This sentence contains many words or concepts which are not clear.
The question is if Lorentz considered a difference between: (1) the velocity of our planet versus: (2) the velocity of our planet through the ether versus: (3) the velocity of our planet through space
This whole sentence raises also a philosophical issue.
Page 136
-
-
-
-
-
-
-
The new transformations constitute the celebrated Lorentz transformations
-
Okay.
-
-
-
-
Chapter 13.
Einstein's Special Theory of Relativity - page 143
-
-
-
Would it not be simpler to adopt a more cautious attitude, deriving knowledge from experiment rather than trying to reconcile experiment with a series of a priori beliefs which, for all we knew, might be totally erroneous?
-
Exact.
But what is the reason why Einstein so often uses thought experiments? Even quantum mechanics uses thought experiments. For example: The Schrödinger's Cat Paradox.
See also page 202
-
-
-
-
-
-
-
-
Page 144
-
-
-
-
-
-
-
Hence, Einstein postulated his special principle of relativity, according to which Galilean motion through the ether or space is meaningless
-
Under construction
-
What is called the special theory of relativity concerns the rational consequences that must follow from the special principle.
-
Okay.
-
-
Page 145
-
-
-
-
-
For instance, if in any two Galilean frames at relative rest, two identical clocks and two identical cubes are placed and if then the two frames are set in relative motion, either observer would discover as a result of his measurements that the other man's clock had slowed down and his cube had become flattened in the direction of relative motion.
-
This experiment only makes sense if one frame is set in (relative) motion. If that is the case only the clock in the frame set in motion will slow down. This will be demonstrated when the motion of the frame will be reversed and the two clocks meet again.
-
-
-
To avoid confusion, the appellation Einstein-Lorentz or Lorentz-Einstein transformations is accordingly often made use of.
-
Okay
-
-
Page 146
-
-
-
As Maxwell proved many years ago, a necessary consequence of the laws of electromagnetism was that light waves in vacuum in the stagnant ether should travel with a velocity of 186,000 miles per second.
-
See also page 127
-
-
-
-
-
-
-
-
-
Whence the new result: "Light waves must travel with the same speed of 186,000 miles through any Galilean frame when this speed is measured by the observer located in the frame"
-
How?
-
It is this statement which Einstein has called the principle or the postulate of the invariant velocity of light
-
Okay.
-
-
-
-
-
-
-
-
Page 150
-
-
-
The contraction is due solely to a modification in our space and time measurements due to relative motion, and is completely irrelevant to the hardness or softness of the body whose atomic or electronic structure need not to be taken into consideration at all.
-
The question is: why mention relative motion and not relative distance? Or is this one and the same?
The issue is that when the distance increases we observe length contraction and when the distance decreases there is length expansion.
-
In much the same way an object appears magnified under the microscope and this magnification is independent of the body's nature.
-
This sentence is crystal clear about length contraction: it is not physical.
What is not mentioned are both the concepts of contraction and expansion?
-
We have now to consider certain important consequences of Einstein's theory which affect our principal concepts of space and time.
-
Okay
-
-
-
-
Page 151
-
The Fitz-Gerald contraction is no longer a real physical contraction as it was to be in Lorentz's theory.
-
This issue should be supported up by experiment.
-
If the observer remains attached to the body, there is no contraction; if the observer is moving with respect to the body, or the body moving with respect to him, the FitzGerald contraction appears.
-
Exactly what is mentioned with: appears? Is this a visual illusion?
When the distance between an observer and an object increases both the tangential length and the radial length (if visible) of the object appear shorter, but this is not real. It has no physical consequences.
-
-
-
Nothing has happened to the body and yet its length has altered.
-
When any human moves freely through space, all what he observes, his whole vision, everything changes all the time. However all these changes are visible changes and have no physical implications. If this is not the case than the experiments performed should be clearly described.
This whole issue belongs to the category of philosophical issues.
-
-
-
-
Chapter 14.
Relativistic Mechanics - page 156
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Page 158
-
-
-
To illustrate: The nucleus of the hydrogen atom is composed of one proton; and the nucleus of the helium atom was believed to contain four protons and two electrons.
-
Okay.
-
Today, we believe that the two electrons with two of the protons to form two neutrons, so that the helium nucleus is formed of two protons and two neutrons.
-
Okay.
-
It would, therefore, be natural to expect the helium nucleus to be four times as massive as that of hydrogen.
-
What is the meaning of the word 'natural'? Does it mean something like: The first idea?
-
Now accurate measurements proved that this surmise was wrong, for there is a slight deficiency in mass i.e. the mass of helium nucleus is less than four times that of the hydrogen nucleus, the deficiency being about 1%.
-
It is of uttermost importance to explain the details of these measurements. Exactly what is measurement: the mass of a helium nucleus or the energy?
-
Thus suppose four hydrogen nuclei were to combine, given rise to helium nucleus; the fact that a decrease in mass would result would imply that the combination was accompanied by a corresponding liberation of energy, equal in magnitude to c^2 times the mass that had vanished.
-
This is what is called the proton-proton chain reaction. See
https://en.wikipedia.org/wiki/Proton-proton_chain_reaction .
More detail is required.
Page 159
-
Since light is a form of energy, light should posses mass and momentum and exert a pressure over bodies on which it impinges.
-
This sentence is in conflict with the following link: https://en.wikipedia.org/wiki/Photon . There is written: Invariant mass of the photon is zero; it always moves at the speed of light within a vacuum.
The whole argumentation is not very convincing.
-
-
-
-
-
-
-
-
-
-
Chapter 15.
Consequences of the New Space and Time Measurements - simultaneity - page 161
-
In view of the extreme importance of the problem let us recall that the postulate of the invariant velocity of light assumes that a ray of light, in vacuum, will pass through any Galilean frame whatever with the same invariant speed c in all directions, provided this speed be measured by the observer at rest in the frame, and not by some other observer in some other frame, whether Galilean or accelerated.
-
This raises three questions:
- How do you construct (define in space) a Galilean frame.
- How do you know that an observer is at rest in that Galilean frame
- How do you measure the speed of light in that Galilean frame (by an observer at rest)
To calculate the speed you need two clocks in that frame.
See also page 147 for an introduction.
See also page 168 and page 193
-
And here we must recall that classical science, believing in the absoluteness of time, assumed that events which occurred "now" any where throughout space would continue to occur in the same simultaneous fashion regardless of the motion of the observer.
-
First the physical evolution of events (processes) has nothing to do, with the motion, of any observer.
Secondly, classical science described by Newton's law, assumes that throughout space, many events can happen (simultaneous) at the same instant i.e. "now"
-
This belief was equivalent to assuming that a propagation moving with infinite speed with respect to one observer would also advance with infinite speed when measured by any other observer.
-
In classical science i.e. Newton's Law, infinite speed of objects is not an issue.
What is an issue is the direction of the force of gravity. Newton assumed that this force points to the present position of an object. Indirectly this implies that force of gravity acts instantaneous. You can also claim that the speed of gravity is infinite. This is wrong. However this was very clever as assumed by Newton.
-
This belief was equivalent to assuming that the propagation moving with infinite speed with respect to one observer would also with infinite speed when measured by any other observer.
-
This may be true, but completely irrelevant in Classical science.
-
-
-
-
-
-
Page 166
-
-
-
Following Römer's discovery, scientist were compelled to discriminate between an external event occurred and the instant we became cognisant of its occurrence.
-
It is 100% correct to make a distinction between the instant when a distant event occurred, and the instant when this event is locally observed.
-
This discovery led them to recognise that pure intuition could yield us no reliable information on the order of succession and on the simultaneity of external events throughout space.
-
The most important issue is to recognise that external events can be simultaneous. A second important issue is the definition of simultaneous events. My definition is: all what happens at the same instant in the universe. What this implies is that there can never be a cause and effect between simultaneous events, because when there is a cause and effect between two events, this means one is caused by the other, they are by physical reasons not simultaneous.
With this issue intuition has nothing to do.
-
The aim of physics was therefore to decide on some conventional means of determining the simultaneity and succession of external events in a manner compatible with the existence of a common objective universe.
-
The question raised in this sentence is important, but becomes impossible to answer because of the restrictions raised in the second half of the sentence. My suggestion is to replace this by: in the universe.
-
-
Page 168
-
In order to avoid any confusion we shall therefore refer to the simultaneity of external events throughout space as physical simultaneity, reserving the name psychological simultaneity for our awareness of the simultaneity of two sense impressions.
-
IMO it is better to replace the text after: psychological simultaneity, with: for all mechanical or human local observations.
The issue to solve what (and if) is the difference between absolute versus relative physical simultaneity.
See also: Reflection 4 - Absolute versus relative in Newton (Classical) versus Einstein.
-
If these points are understood we may pass to a definite example and investigate how the physicist will proceed when he wishes to determine whether or not two external events occurring in different places are simultaneous in the physical sense.
-
The easiest question to answer is: when two events are not simultaneous. The answer is: when one event is caused by the other event i.e. when there is a physical relation between the two events.
See also: Reflection 5 - Simultaneous versus Not simultaneous events.
-
-
-
Suppose that two instantaneous flashes of light occur at two points A and B on the road; and we wish to discover whether or not the two flashes two flashes were produced simultaneous (always in physical sense)
-
Suppose that the two flashes of light are produced simultaneous were does an observer has to stand in order to see them simultaneous?
- The first step is to agree upon that two flashes happened simultaneous at the same instant in the universe.
- A second step is agree upon that at that same instant an almost infinite number of simultaneous events can happen throughout the whole universe.
- A third step is to agree upon that two simultaneous events can both be the cause of simultaneous events. For example consider two simultaneous events with both generate a light flash, which each propagate in a sphere centred on the position in space where the original event happened.
If that is the case then at each instant there after there exist two spheres. The points on these two spheres define simultaneous events.
- A fourth step is to agree upon that sooner or later both spheres will touch each other at one point and there after have a circle in common.
If the position of the observer at the right moment coincides with the position of this circle he will observe the two flashes simultaneous.
This is complete a physical issue.
See also page 171
-
But suppose now that we stood at the midpoint C between A and B, as measured with our rigid rods.
-
The facts were we stand and what we perceive has nothing to do if the flashes of light are produced simultaneous or not.
-
-
-
If we perceived the two flashes simultaneously (in the psychological sense) should we be justified in asserting that the two flashes had occurred simultaneously in the physical sense?
-
Okay.
-
Classical science answered no; for we were not at all certain that the wave of light was propagated from B to C with the same speed as the wave propagated in the opposite direction from A to C.
-
This is opinion 1
-
Classical science assumed that the unknown velocity of the ether drift caused by the earth's absolute velocity would interfere with our determinations, so that nothing definite could be said.
-
As soon as when the ether drift becomes involved we are on slippery ground.
The problem is that in Newton's time people must have realised that there is an issue related to the speed of light waves in (absolute) space versus our speed in (absolute) space.
If the speed of the light waves is always the same (generated by the simultaneous events A and B) and the positions of the points A,B and C always different (caused by the earth rotation) then it can not be guaranteed that the observer at C will see the two events simultaneous.
-
But the entire situation changes as soon as we accept Einstein's principle of relativity and his postulate of the invariant velocity of light.
-
The whole problems boils down to the issue: What is the physical meaning of the invariant velocity of light? Why is that so important for the laws of physics?
See also page 161
-
We are then in a position to assert that the ether drift, whether it exists or not, can have no physical significance; and that we are therefore justified in assuming that the rays of light are propagated with the same speed in all directions.
-
When you combine the two sentences you get:
Einstein's principle of relativity means that the speed of light is the same in all directions.
What exactly does this mean?
Does that mean that a flash of light propagates in an absolute circle in empty space?
With the cause as it center?
What we know is that the speed of the sender is irrelevant and so is the speed at the receiving end.
-
If this is the case we have a right to conclude that the simultaneity of our perceptions of the two light flashes (in the psychological sense) ensures the simultaneous occurrence (in the physical sense) of the two external events, namely, the two flashes on the road.
-
This implies that when an observer half way between the points A and B sees the two flashes simultaneous the events A and the events B are also simultaneous.
This seems rather strange. Consider an observer half way between two mirrors A and B at a train at rest which generates two flashes in the direction of both mirrors. Such an observer will always see the two reflected flashes simultaneous independent of any speed of the train. Does that mean that always the events a (when the flash reaches mirror A) and event B (when the opposite flash meets mirror B) are simultaneous. ?
-
-
Page 169
-
-
-
-
-
-
At the end of the page:
-
But if now we view the same problem in the light of Einstein's theory and if we remember that an infinite speed is a relative depending on the frame of reference or relative motion of the observer, we find that these opinions are no longer tenable.
-
What means "infinite speed"? This requires an explanation.
-
-
Page 170
-
In short, physical simultaneity and duration which were considered absolute by classical science must now be considered relatives having no absolute universal significance since they vary when computed in frames moving at various relative speeds.
-
If that is true then perform all observations and computations in one frame
-
Suppose that two instantaneous events occur at the same point and the same time in our frame of reference.
-
Okay.
-
The events, being simultaneous and co punctual in our frame, are said to constitute a coincidence of events
-
The meaning of the word co punctual (Webster) is: having point in common, are concurrent.
But then these two events are also simultaneous in every frame. That means this is only one event.
-
The principle of sufficient reason itself should satisfy us on this score etc.
-
The opposite is definitely not true.
-
-
-
-
-
A concrete illustration would be given by a collision between two automobiles.
Here we have two bodies situated at the same point of the road (or thereabouts) at the same instant of time; hence the observer on the road is witnessing a coincidence of events in the road-frame.
-
Okay.
-
Obviously, were he to view these happenings from some passing train, the collision would occur just the same; hence, so far as the train-reference-system was concerned, the two events would continue to constitute a coincidence
-
Okay.
-
From this we see that, in contradistinction to the simultaneity of events occurring in different places, which is essentially a relative depending on the choice of our frame of reference,
a coincidence of events is an absolute, that is, remains a coincidence or a simultaneity in all frames of reference.
-
A collision between two automobiles represents ONE event, and not two. Each and every observer will observe the same. In such a case there is no simultaneity of events involved.
What makes physical sense to discuss, is, for example 10 observers and 10 events, which all happened at different positions. If all these events are explosions, all observers, with different motions, will observe these events in a different order depending where they are.
The question is to predict how observer #11 will observe these 10 events.
The first step is to make this exercise simpler and to use only one reference frame.
-
In the squirming world of relativity something at least must be absolute, and one of these absolutes is found to reside in the coincidences of events.
-
The squirming world of relativity, as described here, depends very much about observations made by different observers.
Of course all these observers, in some sense living in their own world, in their own local bubble, will observe the world different. However the evolution of the universe has nothing to do with all the observers. It should be challenge of mankind to understand the laws of nature independent of specific observations and observers.
-
-
Page 171
-
"There is no meaning in speaking of the same instant of time in different places until we have objectivised time, as it were, by specifying our frame of reference"
-
Specifying one frame of reference is the first step. Objectivising time by using only one clock in this reference frame should be the next step.
-
In both sciences, however, the classical and the relativistic, the coincidence of events remains an absolute, transcending the choice of a frame of reference.
-
No. What important is: how to predict a collision between two cars in advance?
If you have two observers, each observer observing only one car, in some way or another they should meet and exchange information, to make such a prediction.
-
From a philosophical point of view, the discovery of relativity of simultaneity marks a date of the same momentous importance as did the discovery of the Copernican system in astronomy.
-
From a philosophical point of view, it is important if (the definition of) the concept relativity of simultaneity,
is clear.
The same question also related to: the concept of the invariant velocity of light.
-
-
-
-
-
-
-
Consider two observers, one on a train moving uniformly along a straight line, the other on the embankment
-
Okay.
-
At the precise instant these two observers pass each other at point P, a flash of light is produced at point P.
-
Okay.
-
The light wave produced by this instantaneous flash will present the shape of an expanding sphere.
-
That is 'correct'. The question is: what is the exact position of that sphere?
-
Since the invariant velocity of light holds equally for either observer, we must assume that either observer will find himself at all times situated at the centre of the expanding sphere.
-
See also page 168
The central view in physics is based on the concept of experiments. The results of experiments define what can be considered as an absolute truth.
The problem is that certain physical theories (opinions) can not be demonstrated by means of experiments.
In the above experiment there are at least four solutions of the expanding sphere:
- Centred on point P.
- Centred on observer 1.
- Centred on observer 2.
- Centred on a different point
The first question to answer is: at any instant is there only one point which can be defined as the centre of this sphere?
If the answer is Yes then most probably the answer is solution 4.
If the answer is No because the center is at one point in each reference frame.
Postulates overrule in some sense experiments.
See also: Reflection 10 - The collision experiment.
-
The fact is that the spherical surface is constantly expanding, so that the points which fix its position must be determined at the same instant of time; they must be determined simultaneously
-
That is correct. When you do that you must also simultaneously define the centre of this sphere. This is point P.
-
And this is where the indeterminateness arises
-
Okay.
-
The same instant of time for all the points of the surface has not the same significance for the various observers; hence each observer is in reality talking of a different instantaneous surface.
-
That is why; when you want to unravel the laws of nature you have a problem, when many observers are involved, with each observer performing his own uncorrelated observations.
|
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Chapter 16.
Practical Congruence in Relativity - page 187
-
-
-
-
-
-
-
-
Page 188
-
Also let us recall that when we discuss space, we must specify it by referring it to a frame of reference, in particular to a Galilean frame (one in which no forces of inertia are experienced).
-
I would say: A frame in which no gravitational forces are experienced.
That can only be the case if space is considered completely empty i.e. without any objects.
-
Now classical science had never thought it necessary to stipulate that our rods should stand at rest in our frame, but in view of the disclosures of relativity we see that it is essential to specify this condition.
-
Reading this, the only logical conclusion is that in an empty universe there can only be one Galilean frame which is at rest, under the assumption that "at rest" implies that the speed of light in all directions is the same.
The physical implications are that a light flash propagates in a sphere, with the center always at the same position.
The only variable in this Galilean frame at rest is the origin.
All the clocks linked to this Galilean frame at rest tick in the same rate.
-
-
-
-
-
-
-
-
-
For when relative velocity exists between A and B (not relative acceleration), there is no sense in enquiring whether it is A or B which is in motion.
-
How do we know that there exists relative velocity between A and B?
Relative velocity implies that the distance between A and B increases during a fixed time interval (in a Galilean frame).
The question arises if there a limit with which this distance (physical) can increase? I.e. is there a maximum distance?
And if so does this maximum distance increase as a function of the fixed time interval.
-
-
Page 189
-
Yet this rod which is moving in our frame is at rest in some other frame, and in this other frame, therefore, the something again coincides with its shadow.
-
The complication is that when in our frame a light flash propagates in a sphere with a fixed center, then this can not be the case in 'some other frame'.
-
-
-
-
-
-
-
-
-
-
Chapter 17.
The Mathematical Expression of Einstein's Fundamental Premises - page 193
-
If a ray of light is propagated from A to B the postulate of the invariant velocity of light demands that the distance AB measured by us in the frame divided by the duration required (according to the time of our frame) for a light wave to cover this distance, be always equal to c, the velocity of light.
-
How is the distance between the points A and B measured in practice. To be more precise: What is a ray of light.
See also page 161
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Page 194
-
-
-
-
-
-
-
These rules of transformation are given by the Lorentz-Einstein transformations
-
Okay.
-
-
-
-
Chapter 18.
The Discovery of Space_Time - page 195
-
The discovery of this invariant:
-
dx^2 + dy^2 + dz^2 - c^2*dt^2
This value we shall designate by ds^2, which marks a date of immense importance in the history of natural philosophy.
-
ds^2 indicates a distance and any distance is always an invariant.
See also: page 90
-
It mattered not whether we were situated in this frame or in that one; if ds^2 had a definite value when referred to in one frame, it still maintained the same value when referred to any other frame.
-
This requires a detailed description how ds^2 is calculated.
Anyway why not use only one frame.
-
Obviously, we were in the presence of something which, contrary to a distance in space or duration in time, transcended the idiosyncrasies of our variable points of view.
-
Of course when you perform physics our (specific my) point of view should be eliminated.
-
This was the first inkling we had in Einstein's theory of the existence of a common absolute world underlying the relativity of physical space and time.
-
Physical space and time is something that exists. (Of course every observers observes differently) The absolute world, reflected by the symbol ds^2, is a calculated mathematical world, which does not exist.
-
Minkowski immediately recognised in the mathematical form of this invariant the expression of the square of a distance in a four-dimensional continuum.
-
This all belongs to mathematics.
-
This distance was termed the Einsteinian interval, or, more simply, the interval
-
Okay
-
The invariance of all such distances implied the absolute character of the metric relations of this four-dimensional continuum, regardless of our motion, and thereby implied the absolute nature of the continuum itself.
-
The definition of a velocity is v = dr/dt = sqrt(dx^2 + dy^2 + dz^2)/dt. What is the difference?
-
-
-
-
-
-
-
-
For these reasons it was called Space-Time, and the interval thus became synonymous with the distance between two points in space-time.
-
But it is not something physical.
-
-
-
-
-
-
At the end of page 195
-
This difficulty however, need not arrest us, for although dt is a time which can only be measured with a clock, yet cdt, being the product of a velocity by a time, is a spatial length since it represents the spatial distance covered by light in the time dt.
-
-
-
-
-
-
-
-
-
Page 197
-
-
-
-
-
Henceforth an instantaneous event occurring at a certain point of our Galilean system and at a definite instant of our time will be represented by one definite point in space-time, a point in four-dimensional space-time is being called a Point-Event
-
Okay.
-
-
-
Now just as an instantaneous event is represented by a point-event, so a prolonged event, such as a body having a prolonged existence and occupying therefore the same point or successive points in the space of our frame at successive instants of time, will be represented by a continuous line called a World-Line
-
Okay.
-
-
Page 198
-
-
-
-
-
-
-
-
-
Thus if two billiard balls kiss in the observation of one man, they will continue to kiss in the observation of all other man, regardless of the relative motion of these men.
-
Okay.
-
The kissing of the balls constitutes a coincidence, an intersection of the world-lines of the two balls, hence it is an absolute.
-
Newton would remark: The kissing of the balls is one event (in the evolution of the universe).
All observers would agree that there is (was) one event.
-
On the other hand, if two billiard balls hit different cushions simultaneously in the observation of one man, they will not in general hit the cushions simultaneous in the observation of a man in motion with respect to the first.
-
Newton will agree with this.
In general each event will propagate (with the speed of light, in time) as a sphere identifying points at the same distance from the event.
The points at each sphere where the two points meet define a plane, perpendicular on a line connecting the two events. Any observer on that plane, at the correct moment will observe the two events simultaneous.
The speed of the observer is not important.
-
-
-
-
-
-
Page 199
-
Owing to the common use of curvilinear mesh-systems in the general theory, we must recall that in a curvilinear mesh-system the square of the interval adopts the more complicated form
-
ds^2 = g22dx1^2 + 2g1k*dx1*dx2 + 2g13 * dx1*dx3 + .....
Expressed more concisely by: ds^2 = Summation gik*dxi*dxk
-
Okay
-
The gik's are no longer constants as when g11 = g22 = g33 = +I and g44 = -I with all the other gik's vanishing: they have now variable values from place to place and as for dx1,dx2,dx3,dx4 these no longer represent space and time differences; they are mere Gaussian number differences
-
The most important question is: how are these gik's calculated in a real application?
See also page 99
-
In spite of all this, the numerical value of ds^2, the square of the interval, remains the same regardless of the mesh-system selected.
-
You get then something like:
-
ds^2 = Summation gik*dxi*dxk = ds^2 = Summation gmn*dxm*dxn
But what is the advantage? You still have to calculate all gik and all gmn values based on empirical facts.
-
-
-
Psychological duration, or aging, can also be represented in space-time.
-
What does the word represented mean here?
-
By psychological duration we mean the flow of time which the observer experiences; or more precisely still, the duration that would be marked out by a clock held in his hand.
-
The concept psychological duration is not a very scientific. It should be called the behaviour of a moving clock.
-
Psychological duration is measured by the length of the space-time world-line followed by the observer.
-
IMO the sentence is not correct. A better definition is:
-
Psychological duration is measured by a clock of a moving observer which is the same as the calculated length of the space-time world-line followed by the observer.
The problem is that the behaviour of not all moving clocks is the same.
See also: page 81 where the behaviour of a clock in a centrifuge is discussed.
See also: Reflection 12 - 1D versus 3D Clock
-
-
-
When we keep this in point in mind the paradox of the travelling twin to be discussed in a latter chapter loses much of its paradoxical appearance.
-
See also: page 443
The twin paradox is based on the physical problem that not all moving clock's behave the same, specific when one stays at home at point A and the other one moves from A to B and back to A.
-
We can also understand how it comes that the discovery of space-time permits us to account for the duality in the nature of motion, relative when translationary and uniform, absolute when accelerated or rotationary.
-
Motion is a calculated quantity, based on positions at different times. When these calculations are not performed using identical clocks fixed to the grid, the results have no common scientific ground and can be observer dependent.
-
As long as we were endeavouring to account for this duality by attributing an appropriate structure to three-dimensional space, we were met by a peculiar difficulty: If we assumed space to have a flat structure, that is, one of planes and straight lines, it would be possible to understand why a free body, when set in motion with any definite velocity, should be guided along one of these straight lines or grooves in space.
-
This whole line of reasoning introduces a philosophical issue: How can you study science by assuming certain concepts which are not true. Any free body moves accordingly to all the masses in space i.e. all the gravitational forces caused by all the objects in space.
-
It would be following its natural course and there would be complete symmetry all around it; everything would run smoothly and no forces would arise.
-
It does not make sense to speak about a natural course, nor is there any symmetry involved. There can be collisions between objects as they travel through space.
-
Then, if we attempted to tear the body away from its straight course, compelling it to follow a curve, we should be forcing it to violate the laws of the space-structure, tearing it away from the space-groove which it would normally follow.
-
Suppose the free moving body is a spaceship and by mechanical means, temporary, you change the speed and course of the space ship. After these events the body again will follow its course, under 'guidance' of all the masses in space. Absolutely no laws are violated. In fact when you change the course of the spaceship, this will have repercussions for all the objects in space.
-
-
-
-
-
-
-
-
-
-
Page 200
-
-
-
But a real difficulty arose when we considered the other species of accelerated motion i.e. variable motion along a straight line.
-
The whole starting point of this discussion is wrong. Always in our universe when there are masses there are gravitational forces and are accelerations. As a result objects moving in straight lines are never really observed.
-
-
-
And yet forces of inertia were again present.
-
To explain the movements of the planets the only force involved are gravitational forces. Of course you can also call them inertial forces, but they are one and the same.
-
-
-
When, however, we substitute four-dimensional space-time for separate space and time, the difficulty vanishes.
-
The concept space and time is wrong as if there exists something as space and something as time. This is wrong. What exist are 3D objects in time. The fact that something exists immediate implies: in time
-
-
-
-
Chapter 19.
The Irreversibility of Time - page 201
-
We saw, when discussing the existence of a finite invariant velocity in nature, that this was going to work havoc with our belief in absolute simultaneity.
-
See also page 171.
See also Reflection 4a - absolute simultaneous versus relative simultaneous. (Relativity of simultaneity)
-
Thus, if two events take places, we can no longer attribute any universal meaning to the opinion that these two events have taken place at one and the same instant of time or at two different instants.
-
The whole issue depends if we recognise that two physical events in the universe can happen simultaneous.
If the answer is "yes" the next question becomes: how are these simultaneous events identified.
-
In other words, there exists no absolute clock giving us the correct time at all points of the universe.
-
This is as we call in the Netherlands: The truth of a cow.
However it would be of utmost importance if such an imaginary clock would exist.
The first question to ask is: Does it make sense to speak about concepts like:
- The state of the universe.
- The state of the universe at a moment in time.
- The evolution of the state of the universe in time.
IMO the answer is: yes.
-
According to the motion of the observer, two events which are simultaneous for one may follow in sequence for another.
-
The first question to answer is: are the two events (at different positions) simultaneous?
- If the answer is "Yes" then there are points which will receive/observe the two events simultaneous.
Such a point should be at the same distance from the two events.
- If the answer is "No" then there are points which will receive/observe the two events simultaneous.
Such a point should be at different positions from the source. Further away from the first event and closer to the second event.
The most important parameter is the position of the observer.
The problem is that what the observer observes is no guarantee in which sequence events happened.
-
-
-
For instance, if two explosions occur at different spots, by adjusting our position as observers it may be possible for us to perceive the two noises now simultaneously and now in succession.
-
What this sentence claims is what we observe can be different depending on the position we are.
That is correct.
However, that does not mean that what we perceive is actually what is happening?
First of all what is meant with perceived?
If this meant "see" than secondly if we see the explosions simultaneous it does not mean that they actually are simultaneous.
-
But such arguments would indicate that the revolutionary notion of relativity of simultaneity had not been grasped.
-
Maybe Yes, maybe No
-
Thus in the example of the two explosions happening in different places on earth's surface, while it is perfectly true that the order of succession in which we hear or see these explosions will depend on our position as observers,
yet, on the other hand, if we take into consideration the time which sound or light waves require to cover the distances separating us from the two explosions, we can always decide without ambiguity whether the explosions occurred simultaneously or in succession.
-
But then you also must specify unambiguous how this time is measured and that is difficult.
-
It was never the order or the simultaneity of our perceptions which was considered absolute in classical science; it was solely the simultaneity or order in which these explosions or events had taken place in the outside world.
-
This sentence is not clear. Our perceptions (observations) are not a good tool to decide what has happened in the outside world.
-
Now, according to the theory of relativity, not only is the simultaneity of our perceptions relative, but in addition, even when we take into consideration the speed with which the sound waves or light waves advance towards us, it is still impossible to decide whether the two events (regarded as existing in the outside world independently of any observer) are simultaneous or not, for our calculations would show that this simultaneity in the outside world would vary from one observer to another.
-
The first question to answer is: Are there simultaneous events in the outside world?
The sentence indicates that the answer is: "Yes", but we humans are unable to decide which events are simultaneous.
Unfortunate the sentence does not explain what the reason is i.e. the actual calculations.
See also page 470
-
Here it is impossible to lay down a rigid rule, for we shall see that the theory compels us to recognise that in certain cases the order of succession is indeterminate or relative to our motion, while in others it is absolute, remaining the same for all observers.
-
As explained on the next page, this issue requires more detail.
To introduce concepts like our awareness, Maxwell's demon and Entropy create scientific doubt.
Page 202
-
-
-
Suppose, then, that in a bottle we place two layers of powder, one white and one black
-
Use a simpler example: throw three dices.
-
If we shake the mixture long enough, we know that the final result will be a uniform grey mixture.
-
The use of the words "we know" is wrong.
See also next sentence.
-
Now we might have anticipated this result without actually performing the experiment.
-
What means anticipated? You might anticipate this when you have observed similar experiments.
In real you should always perform this experiment.
See also page 143.
When you throw three dices long enough you will see that on average you will throw the combination 666, 1 out of each 216 throws. -
For if we consider the various ways in which the particles of the powers could be distributed in the bottle, sufficient reason would urge to us to assert that all distributions were equally probable.
-
You can only assert that all distributions are equally probable, by performing many experiments.
In that case you must give each powder particle a specific number.
That is why it is better to discuss something simpler.
-
But it so happens that by far the greater number of these schemes of distribution would yield the appearance of a uniform grey mixture.
-
The only thing that is true that if you shake the bottle thoroughly 1000 times the most probable distribution observed is a uniform grey mixture.
The same is true that when you throw 3 dices 1000 times the most probably distribution is a mixture.
See also Reflection 9 - The shaking problem - Black White.
-
Probability would suggest, therefore, that on shaking the bottle long enough, the uniform grey mixture would finally appear.
-
Probability has nothing to do with this. The result is completely dependent about the structure of the powder, what is meant
with one shake and the total number of states physical possible. That means it is a physical issue.
See also Reflection 9 - The shaking problem - Black White.
-
We may express these facts by saying that the general tendency would be a passage from the heterogeneous (black and white layers) to the homogeneous (uniform grey mixture)
-
There exists in general not such a general tendency. As said above this completely depends of what you call: shaking the bottle once. Shaking the bottle properly means that each powder particle can go to any position in the bottle.
-
We may therefore identify the states of lesser probability with the past and those of greater probability with the future.
-
No.
When you throw 3 dices each state has the same physical probability. When the powder in the bottle can be considered as having a finite number of states then each state has the same physical probability.
-
The direction of time's passage can thus be defined physically in terms of probability considerations, entailing a mere appeal to sufficient reason to operations of counting.
-
No
-
It is true that there also exist types of phenomena for which all states present the same probability.
-
Correct. Probability defined in the sense as: the same chance of happening in the physical sense.
-
In this case no privileged direction exists and the phenomena are called reversible.
-
It is of no physical importance to make a distinction between reversible versus irreversible. You can not perform any experiment which shows this reversibility.
-
-
-
AS can be gathered from the preceding explanations, a unidirectional passage in the course of phenomena is to be ascribed to the fact that phenomena are irreversible, i.e. that the various states are not equally probable.
-
If the powder particles in the bottle are not of equal size you will observe when you shake the bottle that the larger particles will "float" at the top. This implies that not all states have the same probability. But this tells you nothing about reversibility versus irreversibility.
Page 203
-
To be sure, it would be possible to reverse the process, but only through the medium of some intelligent activity sorting out the particles and distributing them according to states of lesser probability.
-
Any sorting activity, meaning to divide a set of objects based on certain parameters, has nothing to do with states of lesser probability. The only thing that is true that it is easier to bring the state of objects to an unspecified pseudo 'random' state than to a specified predefined state.
-
-
-
Needless to say, however, Maxwell's demon is but a fiction.
-
Then why mention it.
-
-
-
"Heat cannot flow unaided from a colder to a hotter body, but tends invariably to seek lower levels of temperature."
-
This requires a physical explanation about what means: Heat, cold and hot.
-
By introducing a new concept called Entropy defined as the ratio of a quantity of heat to a temperature.
-
It is wrong to define a new concept based on two concepts, for example 'quantity of heat' and 'temperature', which both are not properly defined.
Because of this the next 10 lines are not clear.
-
Thus all natural processes involve an increase of entropy since none are ideally reversible
-
This sentence says nothing.
Page 204
-
Needless to say, the principle holds only when exceedingly large numbers are considered.
-
In fact you need an infinite number of states. But then the concept of probability disappears.
-
In other words, it is a principle governing the chaos, or, again, it is a statistical principle.
-
This sentence says nothing.
-
It will be seen that the principle of entropy, by stating that the world is ever passing from states of lesser probability to states of greater probability, indicates that when the state of maximum probability or entropy is reached, no further change can take place.
-
What exactly is meant with the state of maximum probability?
-
For instance, when shaking the powders, we saw that a uniform grey mixture would be the outcome; but were we to go on shaking the bottle for trillions of centuries, at some time or other the black and white separation would reoccur and the cycle begin all over
-
That is correct and not correct. In principle it is possible when you shake the bottle the next time the black and white separation would reoccur.
-
In short, the entropy would continually increase, but once every trillion years it might suddenly decrease, and then start to increase once more.
-
This sentence clearly demonstrates why the concept of entropy, physical does not make sense.
-
-
-
-
Page 205
-
-
-
For instance, we can readily understand in what an embarrassing situation we should be placed were a reversal of time to occur.
-
No. we cannot understand this. Within the evolution of the universe time has no direction.
It should be explained what this 'reversal of time' physical means.
See also: page 74
-
-
At the end of page 205:
-
When we consider the four-dimensional space-time continuum, where space and time are on the same footing, there is nothing to suggest either a flowing of time or a privileged direction for this flow.
-
What means: are on the same footing?
You can never understand a text, when the concepts used are not clear i.e. 'flowing of time' and 'privileged direction'
Investigating the next sentences the 3 space dimensions and the time direction are not on the same footing. Different rules apply.
-
In order that the theory is conforming to the facts of experience, it is necessary to postulate that our consciousness rises along the world-line of our body through space-time, discovering the events on its course.
-
This sentence indicates this difference: Any object can move in both directions (+x and -x) of each space direction.
In the time direction (mathematical speaking) there is only one direction i.e. forward.
This sentence also raises a different issue: How do you draw the movement of a second object in this space-time diagram assuming that both objects each at certain instances change direction?
Each of these changes for object 1 defines a sequence of events. This is the same for object 2. The problem is the relation between the events of sequence 1 versus the events of sequence 2. See also next page.
Page 206
-
Obviously, we might reverse the presentation by assuming that it was space-time that was moving past our consciousness; we might also claim the very texture of space-time possessed dynamic properties urging our consciousness along time directions.
-
No we cannot. See previous sentence.
-
But in view of the vagueness of the subject, not much is to be gained by speculating on this score.
-
Why mention this? Most of the sentence is not clear.
-
Now when, along the world-lines which each one of us follows, a common direction from past to future has been specified, we find that an absolute past and an absolute future (though not an absolute present) are demanded by the theory of relativity.
-
What does it mean: an absolute past and an absolute future compared to a relative past and a relative future.
This whole discussion is interesting because all of a sudden we use the words absolute and relative.
-
To be more explicit, we find that whereas, according to the nature of our relative motions, certain events may appear as simultaneous, or as antecedent and consequent, or as consequent and antecedent, others will invariable present themselves in the same order of temporal sequence regardless of our motion.
-
This sentence is difficult to understand. To establish the sequence of the events in the universe the first step is to postulate that in general there are simultaneous and non-simultaneous events. The second postulate should be that this sequence of events (assuming that there is a certain relation between certain events), this order has nothing to do with humans in general.
See also: Reflection 10 - The collision experiment.
See also: Reflection 4a - absolute simultaneous versus relative simultaneous. (Relativity of simultaneity)
See also the end of the previous page.
See also the next sentence:
-
This division between events whose order of occurrence is absolute and those whose order is relative is obtained as follows: When ever it is possible for a ray of light to pass from one event to a second event, leaving the first event at the instant it is produced and reaching the second event before or even at the instant at which it is produced, the time sequence of the two events cannot be reversed by relative motion; it is absolute.
-
In fact when that is the case, there is a certain casual connection between the two events and this implies that the two events are not simultaneous. Observers have nothing to do with this.
-
-
-
-
-
Hence we see that when two events are causally connected, their order of occurrence will remain the same for all observers.
-
When two events A and B are causally connected, I assume that there exists a (causally connected) sequence of events, which leads from A to B.
-
Only when no casual connections could possibly exist can the temporal sequence of events be reversed by an appropriate motion of the observer.
-
How do you know that there can be no casual connection between two events?
The issue is, that in case there exists no casual connection (because the large distance involved), if two events still can be simultaneous?
-
-
Chapter 20.
The Reality of Contraction of Length and of the Lengthening of Durations - page 208
-
Consider a rigid rod placed on a table and suppose that both table and rod are drawn away from us with constant speed along a straight line.
-
Generally speaking that in such an experiment there is always acceleration involved.
A much more interesting question arises if the train moves (around us) in a circle.
-
The contraction of lengths implies that both rod and table will appear to us to be contracted, owing to their relative motion with respect to us.
-
When a train (a rod) moves away from us, which implies that the distance increases, we will observe that the train becomes smaller and smaller.
Next, after a certain time, the train will stop. Next the direction is reversed and the train will move towards us. We will observe that the train becomes larger.
Neither the train, nor the people on the train are contracted.
-
Here we must emphasise the fact that this contraction has nothing to do with the motion of the rod through space or the ether.
-
That seems reasonable. The contraction, observed when the train moves away, is pure a visible illusion
-
-
-
-
-
-
-
Page 209
-
-
-
In Einstein's theory, the rod is contracted, but we must add that this contraction holds only in the space of a frame with respect to which the rod is in motion.
-
Suppose you have two observers A and B and each have a rod. The two observers are moving away from each other.
Then
- Accordingly to observer A, observer B is moving away and his rod is contracted.
- Accordingly to observer B, observer A is moving away and his rod is contracted.
The through question to answer: What happens with the rods which mark the distance between the two observers?
Are they also contracted?
-
Only when we consider the contraction from the impersonal standpoint, from that of space-time, without mentioning the conditions of observation, is the Contraction not an illusion, but downright meaningless; for in space-time length itself is meaningless.
-
This sentence is not clear. If in space-time the length of something is meaningless, why mention it?
A concept like space-time is also not clear. Is space-time a physical concept or a mathematical concept?
You can claim that the concept of length of a rod is unambiguous (not clear). However, in principle, you can call the length of any rod the standard (length). When you do that, the sentence: "The length of this rod is 10 times the standard (length)" becomes unambiguous.
-
-
-
-
-
-
Page 210
-
All these arguments developed on the score of length apply in similar fashion to duration. Both length and duration are relatives having no absolute significance in the universe.
-
See Reflection 3 - Length contraction.
-
Just as the height of the man is independent of our position and of our existence as observers, so is the length of the rod independent of our relative velocity.
-
That is almost okay.
It should be mentioned that when we want to measure a rod which is moving away, its length is shorter than it really is and when the rod is moving towards us its length is longer than it really is. The cause is the speed of light.
-
-
-
This length enters into existence only when a definite space is specified; till then it is meaningless.
-
Suppose what is the case when the rod travels from A to B, along a straight path, indicated with identical rods?
-
And in the absence of an observer there is no such thing as space, but merely four-dimensional space-time.
-
-
Thus suppose that, as measured in our Galilean frame of reference, two flashes occur at points A and B situated at a distance l apart and suppose the flashes are separated in time by an interval t.
-
Okay. However, how is the distance between the points A and B measured? Are they physical connected? Similar questions should be raised for the time interval.
See next line.
-
If we change our frame of reference, both l and t will change in value, becoming l' and t' respectively, exhibiting by their changes the relativity of length and duration.
-
The most important question is: Why would you do that Why not study the whole of the universe from one reference frame? This is already difficult enough.
-
-
-
-
-
-
-
-
-
-
-
-
Page 211
-
In the case of accelerated frames, however, we must restrict our attention to Einstein intervals of infinitesimal attitude, and then add up the intervals when finite magnitudes are involved.
-
When you study the solar systems from different frames, with origins linked to points at the surface of the Sun and the planets, then all these frames are accelerated frames.
This creates huge complications?
-
-
-
-
Chapter 21.
The Paradoxes associated with Space-Time and the Trip to the Star - page 212
-
The inevitable rational consequences which follow with mathematical certainty when once the existence of space-time as a model of the universe is conceded, are often puzzling to beginners, who feel that these consequences are too paradoxical to be acceptable.
-
The first step is to define all the concepts used.
-
-
-
If, therefore, when analysing any given example in Einstein's theory, etc, etc and find them to be contradictory, hence inconsistent, the theory of relativity could never survive.
-
The fact that the results of two alternatives are different does not mean that the logic (reasoning) involved is wrong.
-
-
-
But once more it is important to differentiate between strangeness or paradoxes of feeling and inconsistency or paradoxes of reason.
-
Generally speaking in physics there is no place for feelings. The only exception is that it is only humans who have feelings, in the sense those humans are the only objects which question there own existence.
In physics there is also no place for paradoxes only for observations and reason
-
-
-
-
-
-
-
To-day Einstein has done for space, time and motion what Riemann and Lobatchewski did for geometry of space alone.
-
-
-
Page 213
-
Many people, however, are of the mistaken opinion that the theory of relativity leads to paradoxes of logic or inconsistencies.
-
The only thing that is important that the theory of relativity is in accordance with all observations.
-
In many cases the critics seem to have a very hazy idea of the premises on which the theory is built.
-
It is very important to explain these premises very clearly.
-
-
-
Let us consider, for example, the relativity of duration.
-
-
A number of clocks or atoms which beat at the same rate and mark the same time when placed side by side are displaced along different routes to the same terminal point.
-
Okay.
-
The relativity theory then demands that when set side by side once again they shall be marking different times.
-
Relativity theory demands nothing. The question is: what is the result of an actual experiment?
If the experiment involves two clocks and one clock stays at home and the other clock one moves a certain distance away and returns it is easy to show that the elapsed time of the stay at home clock is longer than the elapsed time of the moving clock. This prove is based on the internal operation of the clock.
-
The critic immediately exclaims: "This is inconsistent".
-
The result of an actual experiment can never be inconsistent.
-
There would be inconsistency, indeed, had Einstein started out by positing as an axiom that time was absolute.
-
Any claim that time is either absolute or relative requires a clear definition.
It is very important to make a difference between the concept of time and clock reading i.e. the number of counts on clock.
-
This, in fact, is precisely what the critic has done.
-
?
-
-
-
Of course, the source of all the trouble lies in the fact that a belief in the absoluteness of duration has become second nature to us and it requires a certain effort of introspection of our part for us to realise that this belief presents no rational justification.
-
The only thing that is absolute related to time is the time since the Big Bang.
-
Our sole means of settling the problem is, then, to appeal to experiment; to ultra-precise experiment in the present case, since the crude variety would not enable us to reach a decision.
-
Experiments are the only way to find out how the physical world operates.
Any way if a moving clocks runs faster or slower than a stay at home clock does not mean that duration is either absolute or relative, it only means that this particular clock runs faster a slower than a stay at home clock.
At the bottom of this page:
-
Unfortunately, as we mentioned previously, this experiment with clocks or atoms cannot be performed with sufficient accuracy, so that indirect methods must be considered.
-
Like?
-
-
-
-
-
-
-
-
Page 214
-
But it is precisely because of all the indirect experiments thus far attempted have yielded results incompatible with the absoluteness of duration and distance that Einstein was compelled to reject these secular beliefs of mankind.
-
Please describe one indirect experiment that rejects the concept that duration is absolute.
-
-
-
Let us abandon these generalities and consider the clock experiment in a more vivid form.
-
Okay.
-
We refer to what is known as the problem of the twins.
-
The twin paradox is in essence the same as the clock experiment. See next sentence.
-
In this we consider twin brothers one of whom remains on earth, while the other steps on to a magic carpet and visits distant Arcturus.
-
This is exactly the same as a stay at home clock versus a moving clock.
-
On his return he finds his brother has grown old and decrepit, while he himself has preserved his youth.
-
Using the clock analogy, the stay at home clock shows 1000 ticks and the moving clock 10 ticks.
-
-
-
Now, in order to avoid any misconception, we may mention that in our example both twins hold in their hands clocks which, when placed side by side, beat out their seconds and minutes in perfect unison.
-
Exactly the same as previous mentioned.
-
-
-
Some critics, such as Bergson, while accepting the postulate of the invariant velocity of light, deny that this slowing down in beatings of the moving clock is required by the theory in any real sense.
-
A more detailed description of exactly what Benson means is required.
The whole issue that the moving clocks moves slower is primarily a physical issue i.e. the internal operation of the clock.
-
It is a mere appearance, Bergson maintains; a mathematical illusion.
-
If experiments demonstrate that moving clocks run slower it can never be a mathematical illusion.
-
-
-
Now, it cannot be stressed too strongly that this interpretation of the problem is worse than incorrect.
-
This is a dangerous type of reasoning. The fact that someone else is wrong does not demonstrate that the other party is correct i.e. that Einstein is correct.
-
Not only is it incorrect from the standpoint of Einstein's theory, but it denotes on the part of the critic a colossal ignorance of the significance of a theory of mathematical physics.
-
The whole issue has nothing to do with mathematics. It is a physical issue.
-
Here it must be recalled that the comparative retardation of the travelling twin's clock is an inevitable consequence of the Lorentz-Einstein transformations.
-
No. The behaviour of a clock is a function of how the clock operates. This operation can be described by the Lorentz-Einstein transformations. Other clocks are described differently.
-
-
-
-
-
-
Page 215
-
-
-
-
-
-
-
-
-
-
-
-
Page 216
-
-
-
-
-
Let us now analyse the problems of the two twins, and let us suppose that we as observers are stationed on the earth, say, at the North Pole.
-
Okay.
-
To a high degree of approximation we may consider ourselves, therefore, as at rest in a non-rotating or Galilean frame.
-
-
-
-
-
Page 217
-
-
-
-
-
-
-
-
-
-
-
-
Page 218
-
-
-
In other words, the so-called slowing down of time in the frame of the travelling twin would be due entirely to the slowing down, not of time, but of the optical clock wherewith he proposed to measure time.
-
Implying the slowing down is a physical process, depending about the inner operation of the clock?
-
-
-
-
-
Einstein starts with the assumption that Galilean motion through the ether is relative.
-
What is relative is the motion between two Galilean frames (if they meet).
-
From this it follows that no observer attached to a Galilean frame can be in any means whatsoever ascertain whether his frame is in a state of uniform rectilinear motion or in a state of rest (SR)
-
From this it follows that only one observer (when they meet) can claim that he is in a state of rest.
-
Then he lays down his famous postulate on the invariant speed of light (300.000 km per sec) through any Galilean frame when measured by the observer attached to the frame.
-
How is the speed of light measured?
-
This postulate, as we have seen, enables any Galilean observer to construct an optical clock and to measure duration as referred to his clock, hence to his frame.
See also: page 216
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Page 221
-
-
-
-
-
Our awareness of the flight of time is probably the most fundamental fact of consciousness and it remains an ever-mysterious enigma.
-
All of this is true, but irrelevant in the topics discussed. Personal, human feelings should not be discussed.
-
-
-
-
-
-
Page 222
-
-
-
The fundamental reason for all the criticisms we have mentioned, is that deep down at the bottom of his heart the critic wishes to preserve, in spite of all, his hereditary belief in the absoluteness of time.
-
The concept of absolute time only makes sense if there also exists something as relative time.
What is wrong in the concept that the age of the universe is absolute and that clocks who measure this age are also absolute? Such a clock we can call a universal clock.
What is wrong in the concept that duration is relative i.e. the difference between the two readings of one universal clock?
You can use the same reasoning between the concepts position and distance.
Positions are measured or observed and are absolute. Distances are calculated and relative.
Because both concepts "speed" and "acceleration" are based on the concept distance you could also call them relative, but what is in the name.
The real issue is: how "the age of universe" and "positions in total space", each are measured.
|
-
-
-
In this way he proceeds to draw a distinction between time lived and time measured by our optical clock.
-
To make such a distinction is wrong; however time measured by an optical is also open for different interpretations, specific because not all optical clocks show the same time under different conditions.
-
-
-
For all these reasons, if we accept Einstein's premises there is no alternative but to recognise that the duration marked out by an optical clock in a Galilean system will give us the same measures of duration as will any other isolated periodic physical phenomenon; and that our aging, our awareness of the flow of time, and the time we are conscious of living accompany the oscillations of the optical clock.
-
-
-
-
Under these circumstances, to what does the example of the two twins finally reduce?
-
Okay
-
Simply to this: The departure of our twin brother and his return to earth constitute two definite events.
-
In real there are three events: The turn around event.
-
The duration separating two events being robbed of any definite value by the theory of relativity, there is no cause to be surprised that this duration should manifest different magnitudes to different observers.
-
The reasoning in this sentence is wrong. The observations come first and the explanation second.
We can never be surprised that different observers observe the same process differently. The question is what is identical and what is involved to make that decision.
Only when we have a mutual agreed description of the processes involved we can unravel the laws that describe the same more detailed.
-
Again let us put the paradox in the following alternative form: Our twin brother covers a distance of 20*Sqrt(3) light years (when he goes to the star and returns), and the duration of his trip is forty years; hence his speed along the distance is 20/40*sqrt(3) = 0.5*sqrt(3) that of light.
-
That is a simple calculation, but how do we know that. What are the observations? What are the observed positions and what are the observed events?
-
-
-
-
Page 223
-
-
-
The critic does not grasp the fact that the distance from earth to star, just like any distance, is indeterminate and has no meaning in itself.
-
What does it mean: "has no meaning in itself"?
The word distance means something when you clearly explain how a distance is measured. The problem with any distance, between free falling objects is that the distance is not constant.
To claim that the distance between two objects is equal to "the distance that a light ray travels in one year" does not solve this issue.
-
While it is true that, so far as we are concerned, this distance is 10*sqrt(3) light years, yet in the opinion of the traveller it is only one half as much, and his opinion expresses exactly the same measure of reality as does our own.
-
If two observers don't agree about something they have to compare detailed observations and calculations to solve the issue.
-
We can only repeat once more that absolute duration and distance are incompatible with Einstein's premises, and if we insist upon preserving our classical obsessions, a study of Einstein's theory will be little better than a nightmare.
-
That is maybe true, but the relation with the previous sentence is not clear.
When the traveller uses absolute duration and distances and we not, we have to explain how this explains our discrepancy.
In a second phase we also should explain why our methodology is better.
-
-
-
-
-
This criticism is based on false premises.
-
Okay
-
The Special Principle does not state that when two bodies are in relative motion we may always consider either body indifferently as being at rest and the other in motion.
-
Part of the issue is: what exactly means at rest.
-
The special principle states explicitly that reciprocity of motion exists only when the motions of both bodies are Galilean; in other words only when both bodies remain permanently attached to Galilean frames
-
This first of all requires a definition of the word reciprocity.
Accordingly to Webster dictionary the word reciprocity means: being reciprocal or mutual dependent.
My interpretation is that both bodies should be freely moving, far from any object, with a constant speed.
This is not the case in the twin paradox where always accelerations are involved.
-
When a body is not permanently attached to a Galilean frame, it is must be in a state of acceleration (according to the special theory), and so that reciprocity of motion is no longer valid.
-
This may be true, but it does not explain the twin paradox.
It should be mentioned that in reality all objects are always in a state of acceleration. In fact you cannot perform any (?) experiment without acceleration.
-
Now in the example of the twins, the earth-twin remains fixed in a Galilean frame (if we neglect the earth's rotation and its accelerated motion along its orbit) but the second twin, on reaching the star, changes his position from one Galilean frame to another which is moving in the opposite direction, and so the second twin does not remain fixed to a given Galilean frame.
-
This reasoning is tricky. Initially both twins are in the same reference frame. When the experiment starts there is already acceleration.
-
It is this change in Galilean frames (accompanied as it is by acceleration) which differentiates the present problem from the usual ones studied in the special theory of relativity and which is responsible for the absence of reciprocity.
-
Why this blame on reciprocity? See also next page: page 224
-
-
-
-
-
-
-
-
Page 224
-
In short, the twin that has been subject to acceleration, and so to forces of inertia, will be the younger of the two when the twins meet again.
-
When you perform the experiment twice with optical clocks, first over a long distance and second over a distance twice as long we will observe that the moving clock runs behind twice as much. When you study this more carefully, this running behind is a function of the distances involved. In all these cases the accelerations are the same. In fact this period can be considered very small and don't influence the number of ticks of the clock. What is different is the speed of the moving clock during the whole travel period, versus the speed of the stay at home clock. It is this speed that influences the behaviour of the clock. The maximum speed is the speed of light. When the moving twin approaches the speed of light the optical clock will stop ticking. I expect this is also the end of the story for the moving twin.
In short the explanation of the twin paradox is in the internal functioning or mechanics of the clock.
-
-
-
A body has one velocity or another, according to our point of view of choice of a frame of reference; but when a body is accelerated the choice of our frame of reference is irrelevant for the simple reason that acceleration betrays itself by physical forces and stresses which may exert palpable influences.
-
The explanation based solely on the internal operation of the clock is much simpler.
-
We must not allow ourselves to be misled by further generalisation of Einstein's known as the Postulate of Equivalence, according to which even an accelerated observer may be considered at rest.
-
See also page 236, etc
-
However, those who hope to discover by this means a logical inconsistency in the theory, will again be disappointed ; for the postulate state expressly that an accelerated observer may be considered at rest only if we assume that a field of gravitation takes the place of the field of inertial forces to which the accelerated observer was submitted.
-
The whole issue is the physical meaning of the Postulate of Equivalence
-
-
-
-
-
-
-
-
-
-
-
-
-
Even in classical science it is not necessarily correct to state that velocities ad up like the numbers of arithmetic.
-
Okay.
At the end of the page:
-
Consider, for instance, the following illustration: If, while we are standing on an embankment, a train moves away from us with a speed v and if a riffle bullet is shot from the train with a speed V, it is not always correct to state that the velocity of the bullet relatively to us on the embankment is vV = v+V.
-
Okay.
Page 225
-
This statement is true only when the velocities of the train and the bullet lie along the same straight line.
-
Of course. If that is not the case a whole different situation arises.
But, and this is important, this is the cherry on the cake, how are the three velocities v, V and vV each individual measured? (In order to test the equation vV = v + V). That means this not so much a mathematical issue, but exactly how are positions and time measured.
- Consider that the train has a speed v = 72 km/hour. That is 20 m/sec. That means the traveltime of the train between two markers 20 meters apart, should be exactly 1 second. Both the 20 meters and the 1 second should be confirmed by experiment.
- Suppose that the bullet has a speed V = 800m/sec. That means the time span of the bullet from firing position until the bullet reaches the target 800 m away, should also be in exactly 1 second. Both the 800 meters and the 1 second should be confirmed by experiment.
- Now we perform the experiment in the train. Observations should show that the distance travelled by the train from the point of firing until the bullet reaches the target is 820 meters. Both the 820 meters and the 1 second should be confirmed by experiment.
When all the three experiments are performed it becomes easy to calculate v = 20m/sec, V= 800m/sec and vV = 820m/sec. That means vV = 820 m/sec = 20 m/sec + 800 m/sec = v + V. As expected.
In this particular case all the position and time 'observations' are performed in one reference frame.
The problem with the equation vV = v + V is, if this equation is valid for all values of the speed V of the bullet and the speed v of the train?
What makes this experiment tricky is that the mechanics that describe the bullet belongs to GR or Newton's Law.
-
If a Galilean frame moves away from us with a speed v and if, with respect to this frame and in the direction of its motion, a bullet speeds with a velocity V, the resultant speed of the bullet might be v+V only provided our methods of measuring a velocity, and those of the observer in the Galilean frame, were identical; that is, provided our measurements of space and time were identical.
-
It is important that velocities are not measured but calculated based on positions and time i.e. clock readings.
-
-
-
-
-
-
-
-
-
-
Chapter 22.
22. Potentials and Forces - page 231
-
-
-
In order this indeterminateness, it is usual to specify that the body on which the force is acting is one of unit mass; it is then called a test-body,
-
The whole idea about a test-body is that the test-body is small and does not influence the external gravitational field.
-
Under these circumstances, we can explore a field of force by placing our test-body in successive regions of space and determining the magnitude and direction of the force which is acting on the body.
-
Correct.
The subject is here a gravitational field.
-
-
-
When we have mapped out the magnitude and direction of the force for every point of space, we are in a position to state that we have determined the lay of the field of force.
-
This methodology introduces two concepts:
(1) only one reference frame is used for the whole of space.
(2) If this mapping should be done simultaneous.
-
In physics we are often concerned with fields of force. The gravitational field surrounding the earth constitutes only one particular illustration
-
In fact this field stretches over the whole of the universe as a superposition of all the individual body masses.
-
-
-
When the direction and magnitude of the force are the same throughout space and do not vary with time, the field of force is called uniform
-
This is only true in principle. However in the whole of the universe this condition does not exist.
In fact fields are only called uniform when they are locally strong and uniform.
-
Uniform fields of force are very difficult to obtain; etc.
-
Uniform fields physical are total unimportant.
-
-
-
-
-
-
-
-
-
-
Page 232
-
-
-
Mathematicians were therefore compelled to take into consideration a new type of abstraction called a potential.
-
A potential is basically a physical term. What is important that it physical represents an average i.e. an average force. Such a concept is not useful for a detailed simulation of the planets around the sun.
See also page 267
-
-
-
-
-
-
-
-
Page 233
-
We have already mentioned the field of force surrounding matter
-
See also: page 231 and page 270
-
This was the gravitational or Newtonian field, and the potential at ever point derived there from was called the Newtonian Potential at the point.
-
The word 'at the point' is slightly misleading, because in most cases it defines an average over a certain area.
-
The distribution of the field of force was known in a perfectly definite manner when the potential distribution was known.
-
The real question is: what comes first: 'the field of force' or 'the potential distribution'?
-
-
-
In fact Newton's Law, which tells us how the field of force is distributed around matter, can also be expressed in an equivalent form by Laplace's Equation in which it is the potential distribution, and no longer the force distribution, that is described.
-
That is not correct.
Starting point is the conservation law which describes that the sum of all the forces is zero. Using observations (in time) and with the aid of Newton's law F=m1*a = G* m1 * m2/(r^2) it is possible to calculate the masses of all the objects involved.
-
-
-
-
-
Thus, consider a disk that is rotating, and a ball rolling without friction on the disk's surface.
-
The concept rotating can only considered from a frame that is not rotating i.e. the earth frame.
This is a very tricky example.
-
If the ball is sent from the centre of the disk to its periphery it will of course follow a straight line at constant speed with respect to the earth or to any other Galilean frame.
-
The word of course is wrong.
That is only the case when the ball is like floating above the disc.
This experiment explains nothing, because it is in conflict with the reality.
-
But then, with respect to the rotating disk itself, its course can no longer be rectilinear or uniform. Instead of following one of the radii of the rotating disk, it will follow a curve it had been pulled sideways by some force.
-
From the point of view of the disk the ball will follow a path in the opposite direction of the rotating disk.
-
-
-
To all intents and purposes, when we referred events to the rotating disk and not to the non-rotating earth (the rotation of the earth being so slow that we may neglect it as a first approximation), the physical existence of a field of force would have to be taken into consideration.
-
Rotation speed of the earth at the equator is 460 meters per second.
The rotation of the earth around the sun is a physical effect considered from the position of the Sun. The rotation of the earth around its axis comes on top. The rotation of a disk (on the surface on the earth) again comes on top.
The first question is: what is the influence of these rotations, with respect to a point at the rim of the rotating disc, in the frame of the Sun, assuming that all rotations are happening in the same x,y plane? The movement of this point is very complicated.
The second question is: and what about the speed of this same point? This speed is also very complicated in the x and y directions.
The third question is: and what about the speed of this point, related to the speed of light? IMO very complicated.
The final question is: and what about the speed of the position of the Sun, related to the speed of light? IMO this is simpler.
-
-
-
The precise type of force we have mentioned is called the Coriolis force; in addition, there also exists another type of force, better-known centrifugal force.
-
The origin of these forces is the force that caused the disk to rotate i.e. a human.
-
Both these types of force are called forces of inertia. It is their ensemble which constitutes the field of inertial force existing in a rotating frame.
-
The same forces exist in the rotating frame of the earth versus the non-rotating frame of the Sun.
The same forces exist in the rotating frame of the Sun versus the non-rotating frame of our Galaxy.
-
All these different illustrations show us that whereas, in a Galilean frame, no field of force exists, yet a field springs into existence automatically as soon as we place ourselves in any accelerated frame.
-
A true Galilean frame, where the speed of an object is 100% constant does not exist.
The simple reason is that stars in our Galaxy create forces, and this force can be small, but is never zero. . This field becomes smaller when we move away from the largest object in our neighbourhood and larger when we approach the largest object in our neighbourhood.
At the end of page 233
-
It is for this reason that accelerated frames can be distinguished physical from Galilean frames; and it is owing to this generation of physical fields of force that accelerated motion must be regarded as absolute, whereas velocity, giving rise to no such fields, yields us no means of distinguishing one velocity from another, hence it is relative.
-
The most important issue is that we make a distinction between accelerated frames and frames with a constant velocity.
The question is why we call the first absolute and the second relative? This is not clear. If you have different frames with a constant temporary velocity also accelerations were involved in the past.
-
-
Page 234
-
Hence it follows that, whereas, with respect to a Galilean frame, the inertial potential is zero at every point, or at least maintains some constant value, in the case of accelerated frames this inertial potential must vary from place to place in the frame.
-
Generally speaking the inertial potential of all different Galilean frames is constant. The inertial potential for all accelerated frames varies and becomes constant when the acceleration stops and drops to zero.
-
-
-
-
-
-
-
Consider a Galilean frame and an object moving freely in this frame.
-
Okay.
-
-
-
If we now examine the motion of this same free body from some definite accelerated frame, all we have to do is to change our four-dimensional space-time mesh-system in an appropriate way.
-
What is the reason to examine this free body in an accelerated frame?
Maybe the answer is that free bodies, in the sense of moving in a straight line don't exist.
-
-
-
-
-
-
Page 235
-
So far the reason for the existence of forces of inertia has been made apparent.
-
The reason of the forces of inertia is induced by something external what is supposed to move.
-
They arise owing to the uneven spread of gik numbers which accompanies all curvilinear mesh-systems (accelerated frames)
-
See also page 99 and page 199 and page 252
-
-
-
-
-
-
-
-
Chapter 23.
23. The Postulate of Equivalence - page 236
-
Einstein's Postulate of Equivalence consists essentially in an identification of forces of gravitation and forces of inertia.
-
A better name for Postulate of Equivalence is Postulate of Unification. The two forces are one and the same.
-
Let us first recall that a field of force is exemplified by a region of space, at each and every point of which a definite force would be found to be acting on a test-body with which the field might be explored.
-
It is important to make a distinction between two types of forces: Continuous forces and instantaneous forces.
Continuous forces are induced by matter. The most important is the force of gravity. Instantaneous forces are temporary. The best examples are forces induced by humans. Only continuous forces can be described by a field, because they are permanent.
-
Several different fields were known in classical science. Electric fields acted on electrified bodies, magnetic fields acted on magnets and both inertial and gravitational fields acted on material bodies in general, whether electrified or not.
-
All of this is correct except the concept of inertial field, which is misleading. See also page 237
-
For the present we shall be concerned solely with the inertial and gravitational fields.
-
It is better first to discuss gravitational forces and then inertial forces, because in any earth based experiment there are always gravitational forces involved.
A billiard ball has a weight, which induces a pressure on the billiard table. This pressure again induces friction and if you want to move the ball you have to give the ball at least enough energy, to overcome this friction.
-
These two species of fields of force were regarded by classical science as of totally different nature
-
The origin of a gravitational force and inertial force are different.
-
Suppose, for instance, that a train is slowing down.
-
The whole experiment involving a passenger and a train can be considered an inertial experiment. There is inertial energy involved to start and stop the train. (As a matter of speaking).
-
As such, the force is obviously real, in that it is experienced.
-
Correct. The observer in the train will feel two forces: One when the train starts and one when the train stops.
This line of reasoning is tricky because it has nothing to do with what an observer experiences. Always the same types of force are at stake.
-
But suppose now that an observer on the embankment views these same happenings.
-
Okay.
-
He will argue as follows: No force is pulling the passenger; but as the train is slowing down and as the passenger's body tends to maintain a constant velocity along a straight line , in conformity with the laws of motion (law of inertia) the net result is that he will overtake the engine unless he holds on to the seat.
-
You can never explain an experiment by referring to any law. It is the experiment that defines the law.
If you want to explain this experiment the first step is to define a rigid object.
A rigid object is an object when you push or pull (use a force) the object the whole object moves without out any deformity. A train can be considered as a rigid body. This implies when you apply a force the whole of the train starts to move (instantaneous).
When inside the train there is a passenger (i.e. second object) the whole train (including the second object) is not anymore a rigid object. If you want to move the whole you have to apply two forces: one to move the train and one to move the passenger. That means the passenger has to do something or he will not move.
If you want to stop the whole you again have to apply two forces: one to stop the train and one to stop the passenger. That means the passenger has to do something or he will continue to move, which can be painful.
-
-
-
-
-
Contrast this situation with that of a stone falling towards the ground
-
In that case two fields are involved: The continuous field induced by the earth and the continuous field by the stone.
-
Here we may refer events to any frame we please but in any case the law of inertia can never be made to account for the stone's motion towards the earth.
-
First of all it is much better to write: for the motion of the two objects towards each other
-
-
At the end of the page:
-
The situation appears to be entirely different from that of the passenger in the train.
-
It should be mentioned that the motion of the train is caused by an engine, by the burning of matter and has nothing to do with the opinion of the passenger in the train or an observer on the embankment.
Page 237
-
And so it follows that we are compelled to conceive a real force, a force of gravitation pulling the stone towards the center of the earth.
-
Again it is much better to write: for a force pulling two objects towards each other
-
Thus it would appear that gravitational force, in contradistinction to inertial force, could not be ascribed to mere conditions of observation.
-
Physics has nothing to do with observations. However to understand physics requires observations (and experiments).
-
It was assumed, therefore, by classical science that there existed around a body like the earth a real absolute field of force, which was distributed radial through space, whereas in the accelerated enclosure the forces were merely fictitious or relative.
-
The use of the words absolute and relative is misleading. Anyway if you want to start or stop a train real forces are involved, but it is misleading to speak about a field.
-
Forces of inertia are generated by motion, whereas forces of gravitation are generated by matter.
-
Both are generated by matter. However to generate motion (i.e. moving a train) you need to transfer matter into energy into motion.
-
-
-
Likewise, in an inertial field, the magnitude of the pull is proportional to what is known as the inertial mass of the body, and in a gravitational field the pull is proportional to the gravitational mass of the body.
-
The inertial force to move an object is proportional to the inertial mass of that object.
The gravitational force induced by an object is proportional to the gravitational mass of that object.
The first part of this sentence raises doubts. See below.
-
Every material body was assumed, therefore, to possess two types of masses, the inertial and the gravitational, corresponding to the two types of fields to which the body would react.
The physical issue is if the inertial mass and the gravitational mass of the same object are the same.
To study both the influence of an inertial force and the force of gravity should be considered. The eventual fields are of no importance.
See also page 240
-
A concrete illustration of the difference between inertial and gravitational mass is given by the following example: Consider a billiard ball at rest on a table.
-
It should be remembered that the billiard ball is not only at rest on the table but causes a certain pressure against the table caused by the force of gravity induced by the mass of the earth.
-
-
We should discover that the more massive the ball, the greater would be the effort necessary to set it in motion, as also to arrest its motion once started.
-
This whole experiment it not symmetrical. To set the ball in motion requires an instantaneous force larger then the friction induced by the pressure against the table induced by the force of gravitation. The extra amount will start the movement, but the friction works as a force against the direction of movement, slows down the movement, until the billiard ball finally will again come to rest.
-
The type of mass with which we should here be concerned would be inertial mass; and we may say that it is inertial mass which opposes a departure from rectilinear uniform motion at rest, hence which opposes acceleration.
-
That is a tricky explanation. The issue is that in order to bring the billiard ball in motion a force should be applied which is larger than the opposing friction (force) caused by the contact the ball and the surface of the table. This friction is a function of the gravitational mass of the billiard ball.
As such to call the inertial mass and the gravitational mass the same seems the most logical.
-
-
At the end of the page:
-
Yet it so happens that the most refined physical experiments have invariably proved the strictest proportionality between these two types of masses; so that by choosing our units suitable it was always possible to represent both the inertial and the gravitational mass of a given body by the same number.
-
Problem solved. But then it can not be called a postulate.
This in some way implies that you cannot demonstrate this equality by means of experiments.
-
-
Page 238
-
Classical science had accepted the equality of the two masses as an empirical fact, but had found it self incapable suggesting any theoretical justification for it.
-
The question is if there are really two types of masses involved or only one.
The only way to solve the issue is by means of an experiment.
When you drop two identical billiard balls from a certain height you will see that the behaviour is identical which implies that the gravitational masses are the same.
(The gravitational mass of the earth includes the gravitational mass of the billiard ball)
When you drop one billiard ball the gravitational mass can be calculated based on observations. In that case the gravitational mass of the earth is slightly less.
When you study the behaviour of a billiard ball on a billiard table also gravitational masses are involved.
-
For suppose, indeed, that the equality did not hold.
-
Okay. Implying that gravitational mass and the inertial mass of objects don't have to be the same.
-
This would imply that two billiard balls might present exactly the same gravitational mass, yet differ in the value of their respective inertial mass.
-
See also: Reflection 11 - Gravitational mass and forces versus Inertial mass and forces
This sentence contains a philosophical issue
IMO there are two possibilities:
- First this sentence means that you can have billiard balls that have identical gravitational masses yet have different inertial masses.
- However a this could also mean that you can have billiard balls that have identical inertial masses yet have different gravitational masses.
This implies that the balls are not physical identical in some way or another. More detailed information is required of the cause of this discrepency.
Anyway inorder to settle this situation, what you need are individual experiments which test either the gravitational mass or inertial mass and not both
-
If then, the two balls were to be released simultaneously and allowed to fall from the same height towards the earth, their gravitational mass being equal, both balls would be subjected to exactly the same pull by the earth.
-
Okay
-
But their inertial masses being assumed unequal, the ball whose inertial mass was greater would oppose the acceleration of the fall more strenuously than would be the case with the ball of lesser inertial mass.
-
This whole line of reasoning is logical tricky.
It can easily be demonstrated that the inertial mass of both billiard balls are the same by applying the same inertial force against each.
A different way is to hang identical balls on identical strings from the same height. A force applied to the left ball will propagate through all the other balls. That means there is frictionless energy transfer between each ball, in agreement with the concept that the mass of each is the same.
-
As a result, the balls would not reach the earth's surface simultaneously.
-
When this is the case there is a problem with both the concept gravitational mass and inertial mass. See also the two possibilities mentioned previous.
There is an issue if falling balls or anything free moving have anything to do with inertial mass or inertial forces
-
It may be mentioned, however, that ultra-precise experiments (notably with Eötvös' torsion balance) have since verified these results with extreme accuracy.
-
The results of what? The equality of masses or the fact that inertial mass and gravitational mass are one and the same?
What ever is the case you need a very precise definition of both the inertial mass and the gravitational mass and how each can be measured separate.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
The statement that all bodies fall with the same motion in vacuum is correct, but, unless properly understood, is apt to lead to erroneous conclusions.
-
In fact this statement 'does not make sense' because nowhere in the universe there exists a vacuum. However this depends what a vacuum is. To call empty space: vacuum, implies that both words mean the same, which raises the question: why?
-
What the statement asserts is that any body, regardless of its constitution or mass, will fall in exactly the same way through a given gravitational field.
-
This of course is not true and depends on the mass of the second object. The issue is that in fact always both objects fall towards each other. And as such influence the gravitational field of both.
-
If, however, the falling body causes a modification in the distribution of the field, then it is obvious that various falling bodies will no longer be situated in the same gravitational field, then it is obvious that various falling bodies will no longer be situated in the same gravitational field; and there is no reason to assert that they will all fall in exactly the same way.
-
For all practical purposes, this is always the same
At the bottom of this page:
-
The motion of the earth would thus shorten considerably the distance through which the moon would have to fall, whereas the billiard ball would have to fall through the entire distance.
-
That is 100% correct.
It is important to remember that we are only speaking here about gravitational mass.
-
-
|
Page 239
-
We see, therefore, that the equality of the two types of masses allows us to anticipate that the observer situated in a falling elevator would have no weight.
-
The last remark is strange. In a falling situation both the elevator and the observer are falling. Only the gravitational masses are involved of both the observer and the elevator.
-
The fact is that both observer and weighing balance would be falling with the same motion towards the earth; hence the observer's feet would never press against the balance.
-
The fact that both are falling with the same speed is the most important.
-
-
-
In short, no mechanical experiment could reveal the presence of the earth's field of gravitation in the interior of any frame of reference moving freely under the action of this field of gravitation.
-
When you drop pebbles (point masses) from a sphere around the earth, they will all drop in straight lines towards the center of the earth, demonstrating that the gravitational field radiates away in the opposite direction, like the stakes of a wheel.
-
-
-
Experiments conducted inside such falling bodies are very difficult to perform, but since the results we have mentioned are the immediate consequences of the equality of the two types of masses, which highly refined experiment has established, we are able to anticipate indirectly the results of such experiments.
-
Which are these 'highly refined experiment'?
The borderline is that experiments inside falling objects are of no scientific importance, because the results can not properly 'measured'
|
Page 240
-
So far we have considered the cancellation of a field of gravitation, but we may also consider the creation of a field of force in empty space far from matter.
-
If an object is inside a free falling object the field of gravitation is not cancelled. Every object is always guided by all the objects in the total universe. This is the case for large and small objects, if they are nearby or faraway.
-
Thus, if a hollow chest be subjected to a variable acceleration through empty space, a variable field of force (inertial force) will be experienced by an observer in chest's interior.
-
I expect the following is meant:
-
If a floating hollow chest in empty space is subject of an external force (motor on top of the chest) an inertial force will be experienced by an observer inside the chest and attached to the chest.
-
-
-
Thus, according to classical science, there existed a very decided difference between the two types of fields of force, and it was always assumed that this difference would be detected when we performed non-mechanical experiments such as optical or electromagnetic ones.
-
The basic whole issue is recapitulated by the difference between two identical large objects in two different situations.
- In the first situation they are kept apart by a fixed length rod. That means we can speak of one object, which each has an inertial mass and a gravitational mass.
- In the second situation this rod is broken. Now we have two objects.
Now we have two inertial masses and two gravitational masses.
The question is does it make sense to make a difference between the inertial mass and the gravitational mass or is it better to speak about one object which shows gravitational behaviour when in a gravitational field and inertial behaviour when in an inertial field?
What will happen in the second situation is that the two masses will collide as a result of the gravitational force between the two objects.
See also page 237
-
-
-
Also in the case of the falling elevator, we should not say that the field of gravitation had been counteracted; we should say that it has vanished.
-
This is typical a local argument.
The gravitational field has vanished when you put a force on the falling elevator which points in the opposite direction as the direction of movement of the falling elevator, such that the distance between the elevator and the floor is constant.
Page 241
-
But, of course, Einstein's idea was susceptible of experimental proof or disproof. For if we assume that the two types of fields of force are all one, we must assume that not alone mechanical experiments, but also all manner of experiments, will fail to detect the slightest difference.
-
This is similar as the perpetual mobile experiment. Please build one to prove that one exists.
-
This is indeed Einstein's attitude, and he upholds it in the postulate of equivalence
-
The philosophical question is: are postulates the correct way to unravel scientifically the laws of physics.
See also: Reflection III - The philosophy of Science, Experiments and Postulates.
-
This postulate states that there can exist no difference in the conditions prevailing in the interior of an enclosure, regardless of whether the field of force experienced be generated by acceleration or by gravitation.
-
The issue is the force of gravity which causes gravitation and the inertial force which causes acceleration.
In the case of gravitation (because it is a constant force) you can define a field, but in the case of an inertial force not, because the duration is instantaneous or temporary.
The masses involved are respectively the gravitational mass and the inertial mass.
The gravitational mass of an object is calculated solely based on observations for free moving (falling) objects. Nothing prevents us, to use the gravitational mass when we study the behaviour of an object when inertial forces are involved.
See also page 237
-
The equality of the two masses proved that so far as mechanical experiments were concerned, conditions existing in a falling elevator would be identical with those enduring in an enclosure floating in free space far from matter.
-
The whole issue is that in physical sense the behaviour of free moving objects in space are only influenced by each their gravitational mass. In such a situation when mechanical experiments are be performed the concept free floating can be jeopardy
-
These anticipations were based on experience.
-
That is maybe true. The whole issue is that first people thought that there are two concepts gravitational mass an inertial mass, but in reality they are one and the same. The difference is in the forces: The force of gravity, inertial forces caused by engines and humans and friction.
-
-
-
It is not his knowledge of mathematics or physics that causes admiration; it is his insight into the philosophy of nature, which is stupendous.
-
This sentence is by itself a philosophical issue. We cannot speak about the philosophy of nature. Nature, the universe, evolves as an open system without any logic. We can only speak about the philosophy of physics i.e. something which involves humans.
-
-
-
-
-
-
-
-
Page 242
-
If we now pass to the problem of gravitation we see that the situation is very similar.
-
-
Gravitational force vanishes in a falling elevator; this is a physical fact.
-
It requires a very detailed description what is meant by this.
When we stand on the ground, on a floor, we feel the force of gravitation.
When we jump, we start falling towards the earth. At that moment we don't feel the force any more, but the force is still there, because the force is the cause that our speed increases linear.
-
Classical science took the stand that the force did not really vanish, but that it was compensated.
-
This sentence requires more detail.
-
Einstein prefers to assume that if the gravitational force appears to vanish, it is because it really does vanish.
-
This sentence contains a strange twist. Gravitational forces are supposed to be induced by gravitons. The sun is such a source of gravitons which propagates throughout the universe in straight line, undisturbed. The situation is the same for the earth and the moon. No physical changes can be detected when the Sun, the Earth and the moon are in one straight line, which 'proves' that the gravitons pass undisturbed through any intervening object. For photons this is different.
-
Just as a force of inertia can be annulled by changing the motion of our frame, so now can a force of gravitation be annulled.
-
This whole sentence is a philosophical issue.
What exactly means annulled? Accordingly to Webster: to cause to cease to exist; reduce to nothing.
Within our universe, within the whole physical realm nothing can be annuled. The forces of gravity are always there because they are an important concept to explain the movement of the planets.
When you are in a merry go round (mgr) first of all you need an inertial force to get the mgr moving. When you are in the mgr you feel an outward force. This is physical because your radius increases. If the mgr all of a sudden stops, which also requires a force you will free fall towards the earth, caused by the force of gravity.
All these forces are physical real, independent from which frame you want to study the physical world.
-
This does not mean that a force of gravitation is unreal.
-
The whole issue is that we humans can feel that we are standing on the surface on the earth, caused by the force of gravity induced by the earth. The question is: are we also aware that the earth is falling through space, in a more or less circular trajectory and that we are part of this process? The answer is no.
But does that imply that the force of gravity caused by the sun is annulled? I doubt that. This force is real.
-
But it is no longer an absolute; it is a relative, like a force of inertia, for its value varies with our choice of a frame of reference.
-
-
Henceforth no intrinsic difference exists between a force of gravitation and a force of inertia; these forces are of the same essence.
-
This depends what you mean by essence. A gravitational force is a continuous force. An inertial force is an instantaneous force but can also be temporary.
-
-
-
-
-
-
-
-
Page 243
-
-
-
Consider a hollow chest pulled by some unseen hand through interstellar space far from matter.
-
Such a situation is physical not possible.
Please study: Reflection III - The philosophy of Science, Experiments and Postulates.
-
If we suppose that the chest is rising vertically with constant acceleration, we know that as a result of this constant acceleration a uniform field of inertial force will be present in the interior of the chest.
-
This example is not very clear. What you can have two identical spaceships which travel with almost identical speeds through interstellar space. One goes slightly faster than they other. What you can do is to turn on the engine of the fastest and give it a boost in the direction of the slower one. By performing that continuous and carefully the result could be that the fastest space ship performs a revolution around the slowest one. In fact now the behaviour of the fastest spaceships becomes a combination of acceleration and gravitation.
-
The postulate of equivalence consists in asserting that the observer in the interior of the chest might with equal justification consist the chest to be unaccelerated or at rest in space, while the field of force he perceives would be assimilated to a field of gravitation.
-
In the case of the two spaceship the postulate of equivalence 'seems to indicate' that an observer in the slowest moving spaceships, which performs no action, also can consider the behaviour of his spaceship as a combination of acceleration and gravitation. All of this reasoning raises certain doubts.
-
All that it is meant here to imply is that the physical nature of fields of gravity and inertia is one and the same.
-
It is clear in the case of the two spaceships that the force of gravity and the force induced by the engine in the fastest spaceship are physical completely different. Only in case of gravity you can speak of a continuous field.
-
-
-
We shall see that when we come to consider the universe as a whole, there maybe grounds for modifying our opinions.
-
When you consider the universe as a whole, the whole universe becomes one frame. The motion of such a frame cannot be changed. See also page 242 .
In order to understand the movement of the stars in our Galaxy; you have to consider the universe as a whole.
-
-
-
-
-
Nevertheless, the inertial field on the disk can be called a field of gravitation for the reasons previously set forth in this chapter.
-
In order to give the disc a speed you need an instantaneous force. After that the speed will continuous diminish because of friction. To speak about an inertial field, does not make much sense.
It makes sense to make a distinction between different types of forces, specific if they are continuous or instantaneous.
-
-
At the end of the page:
-
This statement may appear to be in conflict with the example of the falling elevator, in which it was explained that owing to the motion of the elevator the field of force produced by the earth vanished in its interior.
It does not make sense to claim that the (field of) force produced by the earth vanished in its interior, because when there is a free object within the elevator, this object will also fall for the same reason (force of gravity) why the elevator falls.
-
Page 244
-
-
-
In the falling elevator no field of force is experienced in the interior of the elevator, provided the extension of the elevator is small in comparison with the size of the earth.
-
The elevator falls under influence of the earth. When inside the elevator there is a small object this object also falls under influence of the earth.
From the point of view of the elevator the object seems at rest. However from the point of view of the object the elevator seems at rest.
What is the point? Anyway it does not make sense to claim that something vanishes.
-
-
-
-
-
-
-
-
-
It follows that a falling elevator cannot be assimilated in all rigour to a Galilean frame, since in a Galilean frame, wherever we might be stationed, no forces would be experienced.
-
A falling elevator, towards the earth, is experiencing the force of gravity, implying that this observer is not at rest in the frame of the earth. This is the same for any observer falling towards the earth.
-
-
-
-
-
And so it is not correct to say that it would be impossible for us to ascertain whether the field of force experienced in our enclosure was due to the acceleration of the enclosure or to the proximity of gravitating masses.
-
This means that it is possible. But how important is that?
The acceleration of the enclosure, assuming this is considered a falling elevator, is caused by the proximity of matter i.e. the earth.
-
Even without peering out and discovering whether large masses were present, we could always, at least in theory, by a mere exploration of the field distribution, ascertain the true conditions.
-
How is that done?
-
-
-
In fact, as we shall see later, the complete relativity of all motion can be established only if the universe is finite.
-
See also page 301
-
-
-
Now it might be thought that owing to this fundamental difference in the spatial distribution of fields of force (inertial and gravitational) the postulate would not be much use in its physical applications.
-
This is a philosophical issue related to the definition of postulate. A postulate is the same as an axiom. It is a self-evident statement. The problem with any postulate is that it should be self-evident in all situations where it is used.
Page 245
-
But this view would be erroneous.
-
The issue is that the postulate should be clear whenever used. For example the postulate is also used to explain the bending of light rays.
-
From a purely qualitative standpoint the postulate permits us to assert that any phenomenon whose behaviour should be affected by the acceleration of the enclosure, must also be sensitive to the presence of a gravitational field due to matter.
-
The implication of the postulate could be: that any object whose behaviour is affected by acceleration consists of matter and as such is also sensitive to a gravitational field.
The question is if a free floating enclosure is accelerated does this has any consequence for a free floating object inside this enclosure.
If electromagnetic phenomena are considered the answer is: yes.
When the mass of the enclosure is small and the mass of the object is small the answer is: no.
-
Inasmuch as it is often easy to see that the acceleration of our frame of reference must inevitably modify the observed behaviour of a phenomenon, we are able to infer there from that the same phenomenon will also be affected by a gravitational field generated by matter.
-
A reference frame can not undergo acceleration, only objects can.
-
-
-
-
-
It was by following this matter that Einstein was able to anticipate a number of gravitational effects which classical science had never even suspected.
-
That is correct. The primary issue is first by means of experiment to detect them. The second issue to explain.
-
Chief among these are the bending of a ray of light in a gravitational field, and the Einstein-shift effect, since observed on the companion of Sirius.
-
Specific the bending of light is the most interesting.
-
We may understand without difficulty how the bending of a ray of light was anticipated.
-
You can never understand physical phenomena. You can only understand that given a similar situation (cause) that the results are the same.
-
For consider an enclosure floating in empty space far from matter.
-
Assume moving instead of floating.
-
A wave of light enters by a crack in the wall and travels through the enclosure along a line parallel to the floor.
-
Okay.
-
But if now the enclosure be uniformly accelerated, the floor advances with accelerated motion across the ray.
-
I expected you turn on an engine, which gives a power boost in a certain direction.
-
AS referred to the enclosure, the ray of light will thus assume a bent path, just as the course of a bullet would appear bent under similar circumstances.
-
As referred to the enclosure: yes. As referred to the light ray: No. The path of the light ray is not bended when a force is acting upon the enclosure i.e. undergoes acceleration.
Consider a large collection of parallel laser beams. The enclosure is smaller as this collection as such the enclosure is engulfed in laser beams. When the enclosure, which has one hole, is given an extra speed in a certain direction the only thing that you will observe from within the enclosure, when a laser beam enters through the hole, that the path within the enclosure is different.
The reflection point on the opposite wall will move. However nothing happens with any of the laser beams.
That means the laser beams are not influenced by the speed or extra acceleration of the enclosure.
In fact nothing, free moving, within the enclosure is affected, when the enclosure is accelerated by an external force.
The path of a bullet is bended because a bullet is also like a free moving object, bended by earth gravitation.
-
Then the postulate of equivalence allows us to assert that exactly the same results would have ensued had the enclosure been at rest in a uniform gravitational field; so that regardless of whether or not uniform gravitational fields generated by matter can exist, we are led to the general conclusion that a gravitational field will bend the course of light waves and modify their velocity.
-
The postulate of equivalence can only express what is observed. It can express the behaviour of free floating objects based on their masses. If the behaviour of light beams is identical as when objects (i.e. masses) are involved this implies that light beams have mass and that the speed of light is not constant.
-
-
-
-
-
-
-
-
Page 246
-
-
-
-
-
In a general way, the postulate of equivalence led Einstein to the following conclusions: Inertial mass and gravitational mass being one and the same thing, all forms of existence which posses inertial mass must also manifest weight in a gravitational field.
-
When all objects have both inertial mass and gravitational mass and When inertial mass and gravitational mass are the same the whole principle of equivalence can be 'removed' because it does not have any significance in the behaviour of objects i.e. stellar mechanics.
In that case only word mass remains. In the case of stellar mechanics these masses are calculated based on the positions of the objects involved there by using Newton's law or GR.
|
-
Conversely, all forms of energy must develop a gravitational field.
-
In agreement with the fact that all (baryonic) masses are the physical the same
-
In the following pages we shall show that the postulate of equivalence, which in the present chapter was derived as a generalisation from the equality of the two masses, can be deduced in a purely rational way from the existence of space-time.
-
But if some form of inequality disappears the importance of the postulate also disappears.
-
-
Chapter 24.
24. The Inclusion of Gravitation in the Model of Space-Time - page 247
-
1. No essential difference exists between a field of gravitation produced and a field of inertia produced by the acceleration of our frame of reference. (postulate of equivalence)
-
IMO it seems much more reasonable to write:
-
No mathematical difference exist between the acceleration caused by the force of gravity (induced by matter) and by an inertial force (produced by any engine)
In the case of gravity we can speak of a field of gravitation. The most important different is that the force of gravity acts continuous and an inertial force temporary.
However it should be mentioned that the most important issue of the postulate of equivalence is that the gravitational mass and the inertial mass of any object is the same. (Which, in some sense, eliminates the importance of this postulate)
-
-
-
These are the results which we must weave into the general model of space-time, unless we reject Einstein's postulate of equivalence, and maintain that fields of gravitation produced by matter have no more in common with fields of inertia than they have with electromagnetic fields.
-
Both gravitational fields and inertial fields have physical nothing in common with electromagnetic fields (except maybe mathematically), but this has nothing to with the postulate of equivalence.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Chapter 25.
25. Tensors and the Laws of Nature - page 252
-
-
-
-
-
It may split up space into equal cubes (in which case it is called Cartesian), or again it may be curvilinear and split up space into irregularly shaped volumes.
-
Why would you do that?
See also: page 84 and page 199
and page 235
-
-
-
In all cases, however, we shall assume that these mesh-systems remain fixed and do not vary in shape or orientation once they have been drawn.
-
For a discussion about non-fixed see: page 265
-
-
-
Nevertheless, we always had to view the possibility of having to investigate problems in which Cartesian co-ordinate systems would be impracticable, owing to the curvature or non-Euclideanism of the continuum.
-
In real all applications are that way, including our solar system.
-
-
-
-
-
-
-
-
-
-
Page 253
-
-
-
-
-
Magnitudes of this sort, which transcend in every respect our choice of a co-ordinate system, are known as
scalars, numbers or invariants
-
Okay.
-
But suppose now that we wish to determine the exact orientation of our rod.
-
What exactly means: The exact orientation?
-
Orientation, in contrast to length, has no meaning until some mesh system has been prescribed; for we can define a direction in empty space only by referring it to some accepted system of standard directions at each point.
-
What means: prescribed? In completely empty space there are no reference points, implying that it is impossible to define a mesh system.
When you know the orientation (angle) you are close to know its length.
The strategy followed in this sentence is to answer one question by raising a different question
That means the answer on the question: 'What is the exact orientation?' is: 'What is a system of standard directions?'
|
-
In a general case of a Gaussian, or curvilinear, mesh system, the definition of the three components is less simple.
-
I thought that a Gaussian system is not empty?
-
Whereas the invariant magnitude possessed no components, the directed one has as many components as the space has dimensions, three in the present case.
-
This sentence depends very much about the definition of the word directed. I expect: orientated i.e. having a direction.
-
A directed magnitude of this sort is termed a vector
-
Okay
Page 254
-
-
-
-
-
As these two rules of mathematical transformation, known as the contra variant and the covariant rule, respectively, appeared to be the only consistent ones, it was recognised that there existed only these twp different types of vectors; the so called contra variant vector and the covariant vector.
-
Okay
-
-
-
-
-
-
Mathematicians discovered, however, that there existed a vast array of other types of magnitudes named tensors whose components likewise obeyed rigid rules of mathematical transformation when we passed from one co-ordinate system to another, and which for this reason could be credited, just as truly as vectors and invariants.
-
Okay.
-
-
-
Page 255
-
-
-
-
-
Here it must be stated that the two rules, the contra variant and the covariant, are in certain respects the antitheses of each other.
-
Okay.
-
What one rule does the other undoes.
-
Okay
-
-
-
-
Page 256
-
-
-
In other words, the equality of two vectors at a point of space constitutes an equality which change in our co-ordinate system can never destroy; the equality is thus absolute.
-
The opposite would be 'strange'.
-
Similar conclusions apply to the equality of two tensors at the same point of space.
-
The opposite would be 'strange'
-
If these conditions are satisfied, we see that equations between vectors and tensors, often called vector equations and tensor equations, exhibit the remarkable property of remaining unaffected by a change of mesh-system.
-
This seems logical.
-
-
-
As a result, what we come into contact with - what we measure in reality - is not the vector or the tensor itself, which is absolute, but its components in the mesh-system that we have selected.
-
It are these measurements which are the most important when we want to study the laws of physics.
-
These components are relative, since they change in value when we change our mesh-system.
-
Why would we do that? Why not stick to one mesh-system? Only then it is easy to compare all our observations and measurements.
-
-
-
-
-
-
Page 257
-
-
-
For this reason it is customary to speak of the covariance rather than invariance of vector or tensor equations.
-
Okay
-
The word covariance expresses the fact that both sides have varied in exactly the same way.
-
-
-
-
All these deductions obtained mathematically are in a certain sense self-evident physically when we recall that a tensor, a vector and an invariant represent magnitudes to which an objective existence may be conceded.
-
The point is that a tensor, a vector and an invariant can be used within a physical context, but strictly speaking they are mathematical concepts.
-
-
-
-
The last sentence, bottom of the page:
-
If these mathematical considerations have been grasped, we may pass to physical applications of these purely mathematical discoveries
-
Okay.
-
-
Page 258
-
-
-
In classical science we often come upon invariants and vectors.
-
Okay.
-
Examples of invariants are given by the mass and the density of mass of a body.
-
The mass of a moving train, the engine, is not an invariant.
The density of mass of a certain volume can change continuously in time.
-
Vectors are illustrated by a velocity, acceleration, a force, a displacement; and we may say that in a general way a vector can be represented by an arrow.
-
A vector has both a direction and a length.
-
The simplest physical illustration of a tensor at each point of space is afforded by the state of compression and tension at each point of an elastic medium which has been distorted
-
Okay
-
In the present case the tensor is a second-order tensor, and, furthermore, it is what is known as a symmetrical tensor
-
-
-
-
It can be proved that the gik numbers which we have often mentioned constitute symmetrical second-order covariant tensors
-
See : page 96 , page 199 , page 235 , page 276 and page 281
-
-
-
-
-
-
-
-
Page 259
-
-
-
Since, however, the shape of our mesh-system, through arbitrary in large measure, is nevertheless restricted to certain types compatible with the structure of space within we trace them, these gik's are also representative of the structure or geometry of our space.
-
This last part is not clear. What means: 'structure of space'.
-
For this reason they are called structural or fundamental tensors
-
-
-
-
-
-
In short, we see that the magnitudes in which classical science was chiefly interested were either invariants vectors or tensors.
-
Okay,
-
-
-
-
Page 260
-
-
-
If now we consider the laws of nature, we can anticipate, for two different reasons, that they must be vector or tensor equations.
-
The laws of nature are descriptions of the physical reality, part of which can be in the form of a mathematical notation i.e. equations.
These equations can be very complex depending about the accuracy required.
-
-
-
-
-
-
-
We may summarise these discoveries by saying that all the laws of classical science were vector or tensor laws.
-
That may be true. The most important thing is that all these laws should be in agreement with all observations and experimental results.
-
They remained covariant or unchanged in form when we changed the orientation or shape of our mesh-system while maintaining it fixed in space.
-
When you do that at least one point within each mesh or grid should stay fixed, but not all points.
-
This last point is important; for in classical science, time being absolute and separate from space, it was solely from the point of view of a spatial change in the shape and orientation of our mesh-system that the laws remains covariant.
-
In classical science time is measured by a (absolute) physical clock which does not move through space. In classical science all the points in the mesh-system have the same time. If there is a physical object at each of these points than all the objects have the same time or age.
Of course if there are different moving clocks involved, which don't agree with each other which clock runs correct, you have a real problem.
|
See also page 264
-
-
-
The numerical values of all physical quantities depend on our choice of standard units for measurements of distance, duration and mass
-
The issue is not so much the standard units, but exactly how these measurements are performed.
Distances are by definition relative, duration is also a relative concept, and a mass is not measured but calculated, for example by using Newton's Law based on distances.
Does it matter that distances are relative? If the only way to do science finally needs relative concepts the answer is: No
-
If, therefore, we change our units, if we adopt the minute instead of the second, etc, the numerical values of both sides of the law will be affected accordingly.
-
That seems logical. This sentence shows that standard units are of less importance if you really want to understand physics.
-
This condition is expressed by saying that both sides of the equation must posses the same dimensionality.
-
I.e. both sides must express the same units of measurements. That seems logical.
-
-
-
-
-
-
-
-
Chapter 26.
26. The Principle of General Covariance or of the General Principle of Relativity - page 262
-
We have endeavoured to show that the great change in our views of the world brought about by the theory of relativity arises from the discovery that four-dimensional space-time and not the three-dimensional space and the independent time of classical science correspond to reality.
-
In some sense this is all mathematics.
Such a claim requires clear proof based on actual observations or experiments comparing both situations.
See also page 264
-
-
-
-
-
-
-
Suppose, for instance, that the four-dimensional spatiotemporal background were characterised by some finite invariant velocity C greater than Maxwell's constant c, which is given, as we know, by the velocity of light in vacuum.
-
My own first thought is: no difference.
The issue is what happens with our observations when light is not propagated in vacuum.
-
-
-
The first consequence of this discovery is to prove that C, the invariant velocity of space-time, and c, Maxwell's constant, must be one and the same, since only on this condition will the laws of electromagnetism remain covariant.
-
This discussion becomes to mathematical based, while this is physics.
The laws of physics can never be proved based on mathematical reasoning i.e. the concept covariant.
The question is: what exactly is the velocity C in the concept space-time versus the speed of the propagation c of an electromagnetic field. The first step to answer that question is to define one co-ordinate system.
-
-
-
-
Page 263
-
-
-
-
-
-
-
Now the fact that the laws of nature maintain the same form regardless of the orientation of our space-time mesh-system or frame of reference, suggests that they must be the expressions of relationships between such entities as vectors and tensors in space-time.
-
The pure fact that a certain law is described as vectors and tensors in space and time or in space-time does not make such a law correct.
It's in the details.
-
-
-
In other words, they should be expressible as vector or tensor equations in flat space-time.
-
It should be mentioned if the equations are vector or tensor equations, it does not make these equations correct.
-
-
-
For let us suppose that this erstwhile flat continuum manifests curvature in certain regions.
-
This is the case everywhere in the universe.
-
Under the circumstances, the covariance of the laws of nature should continue to hold regardless of the flatness or curvature of space-time, hence also of the species of mesh-system we might appeal to.
-
Okay.
-
Henceforth it becomes permissible to say that all the laws of nature express relationships between entities of space-time (vectors and tensors); and as a result we are able to extend to space-time the conclusions we arrived at when discussing space in the previous chapter.
-
The question is if this is required for all the laws of nature, without any clear definition what all the laws of nature are. In the broadest sense this are descriptions of identical processes.
-
-
-
-
-
-
-
-
-
-
-
-
Page 264
-
-
-
It must be kept in mind, however that the space-time tensor test cannot aspire us with certainty what the laws of the real world will be.
-
Under investigation. See page: page xxx
-
-
-
-
-
On the other hand, the classical equations of mechanics and with them, Newton's law of gravitation were certainly incorrect, for they did not remain covariant to a change in our space-time mesh-system.
-
Newton's law of gravitation is certainly incorrect because it assumes that gravity acts instantaneous.
The fact how can we claim that a law is incorrect because of a change in mesh-system?
See also: page 260. Study the concept "while maintaining it fixed in space"
-
-
-
We have stated elsewhere that in this way mass was proved to be relative, no longer an invariant, and its value varying according to our space-time mesh-system.
-
This is a very important remark. Using Newton's law mass is a calculated parameter based on observations.
The general equation involved is F= d(m*v)/dt = dm/dt*v = m * dv/dt
When mass is considered a constant, we get: F= m*dv/dt = m * a
When the masses of the planets in our Solar system are considered in principle a variable (in Space-Time?) it becomes very difficult to calculate each.
-
We have also mentioned that the most exacting experimental tests have proved the correctness of the new laws and the fallacy of the classical ones.
What is important to compare the results of an actual calculation of the behaviour of all the planets of the solar system using Newton's Law versus the same using GR and tensor notations?
-
In the special theory, space-time is also considered flat, so here again the tensor symbolism can be dispensed with.
-
This sentence is important because it defines that in the special theory space-time is considered flat. This implies that tensors don't have to be used.
However suppose that space-time is not flat. This must have consequences for the special theory?
Either in these cases SR becomes invalid or requires modifications.
See also: page 269.
At the end of page 264:
-
We have seen, indeed, that the special theory was concerned only with Galilean observers in space far from matter, and we know that observers of this type always split up space-time into space and time through the medium of Cartesian mesh-systems.
-
That is most probable true but is in practice not very practicable. In any form of physics there is always matter involved.
Page 265
-
-
-
These mesh-systems differ from one another merely by their various orientations in space-time; and we pass from one mesh-system to another by means of the Lorentz-Einstein transformations
-
In real applications these transformations are tricky because what is the speed v of an object versus the speed of light
in different mesh-systems.
-
On the other hand, when we come to consider accelerated observers we are dealing with observers who split up space-time with curved mesh-systems.
-
Maybe this whole line of reasoning becomes impracticable. See also next line.
-
Again, when masses of attracting matter are present, space-time assumes an intrinsic curvature which renders the utilisation of Cartesian mesh-systems impossible.
-
Important remark
See also: page xxx
-
Certain particular observers, such as those who are falling freely in a gravitational field, adopt mesh-systems which are approximately Cartesian in the immediate neighbourhood of the observer; but were we to prolong these mesh-systems sufficiently, we should soon discover that they became curvilinear, hence varied in shape from place to place, owing to the intrinsic curvature of space-time.
-
This sentence clearly demonstrates the difficulties/complexity involved in calculating the movements of the planets in our solar system.
-
Thus, in a general way, why it is that when we leave the special theory, where space-time is flat and where the observer, being Galilean, abides by Cartesian mesh-systems, and when we investigate the general theory, where the observer is accelerated or space-time is curved, the Lorentz-Einstein transformations must give place to a more general type.
-
Okay.
-
Under these circumstances the tensor calculus becomes a mathematical instrument of great power.
-
But also causes great difficulties in practice.
-
-
-
-
-
-
-
-
-
-
-
-
Page 266
-
-
-
-
-
-
-
-
-
Furthermore we may very easily confer a relativistic aspect on the theory if we recall that by selecting curvilinear or Gaussian mesh-systems in space-time, we are merely placing ourselves in the position of an accelerated observer, who refers his measurements to some frame of reference , squirming like an octopus and who times events with clocks running wild.
-
See also: page 104/105
-
-
Chapter 27.
27. The Discovery of Einsteinian Law of Gravitation - page 267
-
Thus, in its most general aspect, Newton's law of gravitation defines the intensity and distribution of the gravitational field both inside and outside of matter
-
Okay.
-
Expressed in this form, it is known as Poisson's equation and is written
-
in this celebrated equation, phi represents the potential at each point; grad(phi) is a complicated mathematical expression linking the potential at a point and its value at all neighbouring points; mu expresses the density at each point of the matter producing the field, and k is a constant of proportionality known as the constant of gravitation.
-
That is true, but how is equation (1) applied in reality? How is 'mu' calculated, based on observations?
In fact equation (1) is much more complex as Newton's Law expressed as: F = G*m1*m2/r^2 with r the distance between m1 and m2.
See also: page 232 and page 299
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Page 268
-
Thus we may say that Newton's law of gravitation inside and outside of matter is given by grad(phi)= 4*pi*k*mu, in which mu is zero or has some definite non-vanishing value according to whether we are considering a region outside matter or in its interior.
-
In reality, in the universe, there is no place where mu is zero
-
Now, this potential distribution in Newton's law refers to the distribution through space of one same potential, an invariant in space known as the Newtonian potential
-
To assume that the Newtonian potential is an invariant i.e. constant does not seem correct because mu is a function of every point in space. Except if the density distribution is uniform.
-
-
-
-
-
-
-
Matter, as a source of gravitation, was obviously described much more completely by this tensor than was the case in classical science, where the mere mention of its density of mass was considered sufficient to determine its gravitational field.
-
Density of mass is an average for a region. In order to calculate the gravitational field each object has to be taken into account.
Density of mass defines an average. If you want detail and accuracy individual objects have to be considered.
-
-
-
-
-
It was a second-order symmetrical tensor generally written as Tik and its ten separate components, as referred to any definite space-time mesh-system, defined such physical magnitudes as the density of matter at a point, its internal stresses, vis viva, and momentum in that mesh-system.
-
The most important issue is: how to calculate these ten separate components?
-
Thus, Einstein was in the possession of the right-hand side of the equation of gravitation in the interior matter, that corresponding to 4*pi*k*mu in Poisson's equation.
-
It is important that mu represents an average.
-
-
Page 269
-
It remained to discover the left-hand side of the equation. Owing to the condition of covariance, this left-hand side had to be represented by a tensor of the same order and nature of the right-hand side, hence in the present case, by a symmetrical tensor of the second order.
-
That is of course mathematical correct. The importance is in the physical implications of both sides.
-
Further, it would have to be built up of the ten gik's or potentials, expressing a relationship between these ten gik's at every point and at the neighbouring points
-
Specific this last part shows how complex this physical is.
-
All these tensors served to represent various possible types of structure, geometry or curvature.
-
Specific in the detailed physical implications
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
In a previous chapter we mentioned these tensors. First, there was the Riemann-Christoffel tensor Bikst. It was a tensor of the fourth order, as indicated by the four indices underlying the letter B.
-
Okay.
-
Then there was a second-order symmetrical tensor Gik.
-
Okay.
-
Lastly, there was an invariant of curvature G, no longer a tensor in the ordinary sense of the word.
-
Okay. The importance lies in the physical and observational details.
-
Einstein had still one further clue to guide him
-
Okay
-
Classical science had assumed that at an infinite distance from attracting matter the law of inertia would hold rigorously; that is to say, a body moving freely would follow a rectilinear course with constant speed when referred to a Galilean frame.
-
The problem is that an infinite distance does not exist. In reality any object is always influenced by all the objects in the universe. To claim that an object has a constant speed is only an approximation; its speed will always increase or decrease and is bended.
-
Expressed in the language of space-time, this would imply that at infinite distance from matter, space-time would become rigorously flat, as we had assumed it to be in the special theory.
-
See also: page 264
-
-
-
-
-
-
-
-
-
-
-
-
Page 270
-
Henceforth, the law of potential distribution, or of gravitation inside matter, would have to be (neglecting constant factors
-
Gik-0.5*gik*G = Tik
(Analogous to Poisson's equation); and outside matter, as Tik disappeared, there was left
-
Gik-0.5*gik*G = 0
This reduces to
-
Gik = 0
(Analogous to Laplace's equation)
-
See also: page 295 and page 301
-
-
-
-
-
-
-
We see, then, that in Einstein's theory ten separate equations are necessary in order to define the distribution of the gravitational field in the interior and around matter, whereas in classical science one equation, i.e., Poisson's equation (grad(phi) = 4*pi*k*mu), was sufficient.
-
This gives a hint why GR is much more complex.
-
-
-
-
under construction
Chapter 28.
28. The General Laws of Motion - page 272
-
-
-
According to Newton mechanics, free bodies in interstellar space far from matter, moving under no constraint, always described rectilinear courses with constant speeds.
-
All of that is true in principle. In reality constant speeds don't exist.
In some sense only one free body can exist. The two objects in a binary system are never free.
-
This law was known as Newton's Law of inertia.
-
In fact the origin of fast moving objects in interstellar space is always gravitation.
-
-
-
We remember, of course, that a law of motion of this type remained completely indeterminate until we had defined the frame of reference to which this motion would be referred, and we saw that any Galilean frame answered our requirements.
-
The concept motion always requires a reference frame. The size of the frame used should be as long as the duration of the motion of the object studied.
-
Now it was assumed that Newton's law of inertia was universally valid in the case of free bodies moving under no constraint; when, therefore, the law was found to be at fault in the neighbourhood of large masses of matter, the discrepancies were ascribed to a real force of gravitation emanating from matter and compelling the erstwhile free bodies to move under constraint.
-
It is very tricky to make a distinction between inertial force and gravitation force among free floating objects small and large.
-
-
-
Thus there existed a complete duality between the two types of law and motion, those for free bodies and those for bodies moving under gravitational constraint.
-
This distinction does not make sense in reality. Generally speaking there are no free bodies. What there are except bodies or objects are point masses in order to calculate a gravitational field
-
-
-
-
-
-
-
-
-
-
-
-
Page 273
-
In Einstein's space-time theory this duality is removed
-
Newton's Law is capable to describe the behaviour of all free bodies large and small.
-
-
-
-
-
-
-
-
-
-
Page 274
-
-
-
Were there no guiding field, or metrical field, were space-time completely amorphous, there would be no space and time partitions, motion would be meaningless and inconceivable; even were it conceivable, the bodies would not know how to move.
-
Laws are descriptions of the physical reality i.e. processes. The behaviour of these processes is completely independent of these laws. The explanation of this behaviour is within the details of the processes themselves.
In short: The evolution of processes is not guided by laws.
-
It would appear, then, to be more correct to state, that freely moving bodies can not exist, since all bodies are subjected to the influence of the guiding field.
-
The way this sentence is written is slightly misleading.
In principle all single bodies can move freely. At the same time all single bodies move in some sort of orchestrated behaviour, each body influenced by all the other bodies. This influence can be described as a field.
-
-
-
The important point to understand is that as regards freedom of motion, all bodies in empty space, whether situated in a gravitational field or far from matter, are on the same footing.
-
There exist no empty space in our (visible) universe except if you call all the space inside our solar system, in between the Sun and all the planets empty space. This is misleading because that space is definite not empty.
To repeat, all the bodies are influenced by all the other bodies.
-
The sole difference is that in the neighbourhood of matter, the lay of the guiding field is curved slightly.
The issue is: what is the physical picture of this guiding field.
The influence between two binary objects is rather straight forward when the distance between the two objects is large and the masses involved are small. In that case the revolution time is large and the influence is flat (The present position is influenced by the almost present position of the second object).
The situation changes, when the distance involved is small and the masses are large. The revolution time becomes small and the influence becomes curved. (The present position is influenced past position of the second object)
-
-
It is incorrect, therefore, to invoke real physical pull acting on the body when it moves near matter, and to deny the existence of such a pull when the body is moving in interstellar space.
Any object always influences all the other objects as a function of its mass. This influence diminishes as a function of distance. Interstellar space has nothing to do with this.
-
-
And yet it might be said: "We experience a real physical pull when we stand on earth, whereas we should experience no such pull were we floating in interstellar space."
-
Okay
-
A freely moving body follows, as we have explained, a geodesic of space-time, regardless of whether space-time be curved by the proximity of matter or whether it be flat.
-
This line assumes a lot of concepts, which are already explained earlier and IMO have nothing to do with the issue. What we should do is to explain this question as simple as possible.
The whole issue that two objects in space always be attracted towards each other and the path followed will be a straight line between the center of gravity of each object. The best way to demonstrate is a diver, who performs a free fall out of a helicopter. There should be no wind.
The whole point is that during the free fall neither the diver nor the earth will 'feel' a force. The attracting force of the earth is not felt by the diver and vice versa.
After the landing, assuming the diver survived, then, when the diver stands up, the attracting force of the earth is still there and is felt by the diver as a counter force. This force tries to stick the diver on the surface of the earth.
-
-
-
-
Page 275
-
-
-
-
-
-
-
But we see once again that this force has exactly the same origin as the forces of inertia we discussed previously, so there exists no essential difference between a force of inertia and one of gravitation.
-
Exact.
The problem is that the behaviour of 'freely' moving objects (like falling apples, planets and stars) is controlled by gravity and not by inertia.
Inertia is typical the behaviour of small objects on the surface of a large object.
-
-
-
In short, they are both of them but manifestations of the four-dimensional metrical field or guiding field of space-time
-
The physical problem is that objects influence each other. The issue is: a physical explanation. The introduction of elementary particles, called gravitons, is such an explanation. Photons are the same for processes when electromagnetism is involved.
The introduction of a field is not the same. A field is a mathematical description of the behaviour of elementary particles. The whole issue is, that any field is not something static but dynamic and changes as the position of the source of the field changes. For Newton this was no issue. For Laplace this was an issue.
Chapter 29.
29. The Verification of Einstein's Law - page 276
-
Einstein's law, as we have expressed it, is one of space-time curvature around matter and in the interior of matter.
-
Okay.
-
It is also the law of the distribution of the ten potentials or gik's throughout space-time or again the law of distribution of the four-dimensional metrical field or guiding field of space-time.
-
The real question to answer is: what are the values of all these gik's of the planets of our solar system?
-
But in order to study the implications of the law we may discuss it from yet another angle.
-
It is very important to study the physical details.
-
-
-
Being a law of space-time curvature or structure, we are able to derive from it the precise lay of the geodesics of space-time around matter.
-
That is the question.
The same remark as above: What are the gik's around matter?
To answer that question you need observations, and with these observations you can calculate the gik's.
Using Newton mechanics the similar parameters are the masses of the objects studied. Using observations you have to calculate the initial conditions and the masses of the objects studied etc. etc. etc.
-
Knowledge of the lay of the geodesics around the sun will therefore allow us to determine the precise courses in space and the precise motions along these courses of all free bodies moving in a gravitational field.
-
This should also be the case for all the planets in the solar system.
This may be true in theory, but how do you calculate the geodesics around the sun in practice? You need some form of step by step handbook of how to perform this very complex exercise.
-
When these geodesics are submitted to mathematical analysis, it is found that the courses and motions of the planets should be very nearly identical with those required by Newton's Law.
-
The issue is, how to calculate the movements of the planets in our solar system first with Newton's Law and secondly with Einstein's Law. In the case of Einstein's Law of gravitation the full law should be used, in all its detail for all the planets, without any simplification.
Of course the results should be almost identical as the results calculated with Newton's Law. Except they should be more accurate compared with observations.
In fact this whole exercise starts with a discussion: How to perform observations using Newton's Laws versus Einstein's Law.
See also: Reflection 8 - Newton's Law and the movement of the planets.
|
-
-
-
-
-
There would be slight discrepancies, however, between the requirements of the two laws.
-
I would use instead of requirements the words implications or consequences.
-
In particular, Einstein's law of gravitation would predict that the courses of the planets should be very nearly elliptical, but not exactly so; there should be a slight precession of the perihelion of the planet, increasing in magnitude with the velocity of the planet on its orbit.
-
Newton's Law also predicts that the orbits are not elliptical and precession of the planet Mercury. This precession is caused by all the other planets; however this precession does not reflects the total precession observed.
What is the explanation of this extra discrepancy?
Newton's Law assumes that gravity acts instantaneous, which is definite not the case.
Einstein's Law assumes differently. But what ever the explanation, this can have consequences on the trajectories of all the planets.
-
-
-
-
-
-
-
However, in the following discussion, we shall see that Einstein's law was able to foretell the existence of a phenomenon totally unsuspected by classical science.
-
-
We refer to the deviation of a ray of light in a gravitational field.
-
Newton's Law predicts the same qualitatively.
Light involves energy and energy corresponds to mass, as such both light and mass will behave the same.
A whole different question is to what extend photons influence each other.
-
-
under construction
Page 277
-
Classical science had always assumed that a gravitational field, such as that of the sun, would attract material bodies, but that it would be without effect on light rays, which were considered to be immune from gravitational attractions.
-
How do we know both 'facts'?
-
Had classical science been thoroughly convinced of the identity of two types of mass, it would have realised that light waves must be possessed of gravitational mass, since they were known to manifest the characteristics of inertial mass.
-
This is quite a remarkable sentence
Common sense, based on the postulate between the equivalence between mass and energy, more or less imposes the idea that photons have mass.
The issue is not so much waves but the transportation mechanism of fields, being either electromagnetic or gravitational (including the higgs field), implying energy transport.
-
This inertial property of light rays had been foreseen theoretically by Maxwell and proved experimentally by Lebedew, who detected the pressure exerted by rays of light on a body on which they impinge.
-
See also: http://web.ihep.su/dbserv/compas/src/lebedev01/eng.pdf "Experimental Examination of Light Pressure" door P.N. Lebedev
-
It would have been, therefore, only a step to assume that light rays must manifest gravitational mass, and hence must be attracted by the sun.
-
Okay. However the only way to demonstrate this is by means of experiments.
-
-
-
-
-
Let us now pass to Einstein's attack
-
Okay.
-
Of course, in Einstein's theory, even prior to his discovery of the new law of gravitation, a ray of light would certainly have been bent in a gravitational field in virtue of the postulate of equivalence.
-
It is doubtful if the postulate of equivalence as described in 23. The Postulate of Equivalence - page 236 can be used as an explanation.
It is the equivalence between mass and energy.
-
It is easy to see how this would arise.
-
General speaking it is very difficult to predict how processes behave.
-
Consider a chest, floating vertically in interstellar space, and a ray of light traversing it horizontal.
-
How can something be floating vertically?
This is may be simple in your mind, but very tricky in reality.
-
If now the chest be accelerated upwards along the vertical, the floor of the chest will move with acceleration across the ray and, as a result, the light ray will follow a curved path through the chest.
-
That is not true. The light ray will still follow a straight path. However from a point of view of an observer fixed to the upward moving chest, the light ray (the same with every thing else not connected to the chest, like the light source) will follow a curved path moving downward.
-
But in this case the postulate of equivalence allows us to regard the chest as not accelerated but permeated by a gravitational field; we may infer, there fore, that the ray of light would bend downwards under the action of this field.
-
The postulate of equivalence describes the equivalence between inertial mass and gravitational mass, but that law has nothing to do, how light rays behave. The only extra force involved, is the force that causes the acceleration of the chest (i.e. a type of rocket), but that action has no consequences on the way a light ray behaves.
Different versions of this experiment use an elevator which is falling in the gravitational field of the earth.
In that case the light ray is bended in the gravitational field of the earth, but follows a straight path inside the reference frame attached to the elevator.
-
Hence, the mere qualitative bending of a ray of light in the sun's gravitational field would not vindicate Einstein's law of gravitation and dethrone Newton's; it would merely prove the correctness of the postulate of equivalence and the identity of the two species of masses.
-
The whole issue is: how can we explain, because light rays are bended around an object, that gravitational mass is equivalent of inertial mass. Does this explanation involve the gravitational mass of the sun and the inertial mass of the sun? Or the gravitational mass of a photon and the inertial mass of a photon? Or all the four masses?
-
It is the precise quantitative bending of the ray, as determined by Einstein's law of gravitation, which constitutes the crucial test of the correctness of Einstein's law.
-
If that is the case and a detailed description of both calculations is required.
-
-
-
-
Chapter 30.
30. The Separation of Space-Time into Space and Time in a Gravitational Field - page 279
-
We must remember that one of the fundamental continuum of the world is space-time, space and time considered separately, varying as they do with the observer's motion, have no absolute significance.
-
First of all you need a clear definition of what means absolute.
Secondly for an observer at 'rest' does it make sense to consider space and time separately? What does that mean?
Generally speaking for an observer at rest his surroundings should not change and 'all' what the observer sees should not change. As such observed space is fixed. Maybe with some exceptions.
But what does time means for an observer being at rest?
There are two meanings of the concept of time:
- Physical existence of objects (matter) in time. That definition cannot be separated from all what exists. Static or dynamic.
- Time as measured by a clock. That time is not the same physical existence but reflects the state of an object or process i.e. a clock.
-
It is the law giving the distribution of the four dimensional metrical field of space-time in the interior of matter and around matter.
-
How is this 4 dimensional field in detail calculated? That is tricky.
-
It is true that we may be able to affect some sort of separation of space-time into the space and time of some particular observer and this may enable us to represent the law of curvature of space-time as two separate laws of curvature, one affecting space and other affecting time.
-
-
-
-
This separation, however, is possible only in the event that the masses of the moving planets can be ignored, so that the only field we have to consider is that of the sun, remaining unchanged as time passes.
-
The masses of the planets can not be ignored
-
Fields of this type are called stationary
-
In reality there are no truly stationary fields
-
For non-stationary fields, such as those where the distribution of the field changes with time, the separation into space and time becomes impracticable
-
With distribution, I assume, are meant the masses of the objects which are responsible for these fields. This is the case for the solar system.
-
-
-
-
-
-
-
-
-
-
Page 280
-
We will assume, therefore, that the gravitational field of the sun is stationary, that is, that the masses and motions of the planets do not modify the field to any appreciable extent.
-
That is a very serious limitation. .
This becomes specific visible when you want to study the behaviour of the stars in our Galaxy.
-
We may then proceed to split up curved space-time into space and time of an observer at rest with respect to the sun and non-rotating with respect to the stars.
-
It would be interesting how this is done in real.
-
In this way we shall obtain , first, a purely spatial metrical field, which will be responsible for the measurements of our rods when these are maintained at rest in our frame ; and secondly a purely temporal metrical field, which will determine the behaviour of our clocks or vibrating atoms while these are at rest in various regions of the space around the sun.
-
I expect then what you get is a 3D grid, fixed and centred around the Sun, with at all the grid points a fixed clock. Fixed means at rest.
-
-
-
It thus becomes possible to describe the world-lines of the planets under Einstein's law by representing them as spatial orbits and motions along these orbits; hence we are enabled to check up Einstein's previsions with astronomical observations.
-
And how are these astronomical observations performed?
-
We will first consider the curvature of time alone.
-
The curvature of space is discussed starting at: page 287
under construction
Page 281
-
When Einstein was led to his law of space-time curvature Gik = 0, he never could have recognised in advance that this law would account for the motion of Mercury.
-
Okay.
-
But Einstein, as we remember, introduces a second restriction, according to which, in empty space surrounding matter, none but the structural tensors of space time, the gik's should enter into the law of curvature.
-
What is the meaning of empty space?
-
-
-
Theoretically, Bikst = 0 could also be countenanced; but this law, indicating perfect flatness, would connote the absence of gravitation.
-
Okay.
-
-
-
-
Page 286
-
-
-
-
-
-
-
In short, we now understand why it is that Einstein's law of gravitation deviates appreciably in its effects from Newton's only when we consider bodies moving with velocities approximating to that of light.
-
IMO the most important problem is with Newton's Law is that gravity does not act instantaneous. With gravity is mentioned the attractive force between objects.
-
-
-
-
Page 287
-
-
-
We have said that our separation of space-time into space and time was equivalent to splitting up the metrical field of time and a metrical field of space.
-
See also page 83 i.e. systems of Co-ordinates and distance
<-- Text correct -->
-
Calculation shows hat the results should be identical with those which could be obtained were we to apply rigid Euclidean rods on an appropriate paraboloid of revolution.
-
More detail is required to understand this.
-
-
-
-
-
-
Page 288
-
-
-
Let us now examine another point. The velocity of light in a gravitational field is no longer an invariant, as it was in the special theory.
-
Okay.
-
However, if we were to measure the velocity of light from point to point, displacing ourselves from one point to the next, we should find that wherever we might be placed, this velocity would always appear the same everywhere, owing to the progressive modification in the behaviour of our rods and clocks.
-
How is the velocity of light measured?
-
It would only be when viewing distant points that we should recognise variations in the velocity.
-
This is a very unclear sentence.
The next sentence is clearer, but the question is if the sentence is correct.
-
When we measure the velocity of light in increments over a long distance than for each increment the velocity is the same. When we measure the velocity of light over this same distance, 'in one go', the velocity will be different.
The impression is that this is the case when the light ray is bended around an object i.e. mass.
-
Thus we see that the principle of the invariant velocity of light is accurately true only in free space far from matter, and even then, only computed with reference to our Galilean frame.
-
What this means that in practice, if you want to understand Celestial Mechanics, the concept that the speed of light is constant, is not true
-
In an accelerated frame, as in the neighbourhood of matter, the cornerstone of the special theory of relativity no longer applies.
-
This sentence has large implications.
-
It follows that in the general theory the law of the invariant velocity of light must be replaced by some more general principle, comprising the invariant-velocity principle as a particular.
-
What this means that a description of how light behaves is very complex. This has serious consequences for all observations
-
This more general principle can be expressed by saying that a ray of light moves along a world-line which is a very particular kind of geodesic call a null-line or minimal geodesic.
-
This more general principle does not solve any issue, but creates a new one: What exactly is a null-line.
-
-
-
-
-
-
-
-
Chapter 31.
31. The Principles of Conservation - page 291
-
-
-
One of the first triumphs of the special theory of relativity was to prove that mass, just like time and space , must be a relative; and that a body in motion with respect to the observer would increase in mass in all ways identical with that disclosed by Bucherer's experiment.
-
This sentence is wrong in the sense that Bucherer's experiment shows that the mass of an electron increases as a function of its speed in agreement with the special theory of relativity.
-
-
-
-
-
Calculation then showed that the mass of a body would become infinite when the velocity of the body reached that of light; for this reason no material body could ever move as fast as light.
-
This sentence causes what is called a philosophical issue. The calculation of mass is wrong, because the result of the calculation is not in agreement with the result of any experiment.
To calculate the mass of an object, Newton's Law or the General Theory of relativity should be used.
General speaking if you want to move an object as fast as physical possible, the object will disintegrate.
-
Now when we discussed mass in Chapter XIV
-
See 14. Relativistic Mechanics - page 156
Page 292
-
-
-
-
-
We remember that assuming the correctness of Einstein's view of gravitation as being due to space-time curvature, the principle of stationary action led us to the law of gravitation.
-
Gik-0.5*gik*G = Tik
-
See also: page 295 and page 301
-
-
-
-
-
-
-
-
Page 293
-
-
-
-
-
-
-
Thus a body falling freely towards the earth can certainly not be said to posses a constant vis viva, or energy, since, originally starting from rest, it acquires an increasing speed as it falls towards the ground.
-
Both objects are originally at rest and both acquire an increased speed as they move towards each other.
You can also perform a different experiment: Original the object is at rest at the surface of earth. You pick it up and you drop it. The amount of energy to pick it up and the amount of energy of the object just before it touches earth are the same.
-
-
-
-
Chapter 32.
32. Other Aspects of the Gravitational Equations - page 295
-
-
-
-
-
-
-
Now, In Einstein's theory, the gravitational equations become
-
Gik-0.5*gik*G = Tik
Where Gik and G refer to the curvatures of space-time, or if we prefer, to the potential or gik distribution, while Tik represents the characteristics of the matter exiting the field.
-
See also: page 292 and page 301
-
-
-
-
-
-
-
-
-
-
Page 297
-
-
-
-
-
-
-
-
Chapter 33.
33. The Finiteness of the Universe - page 298
-
-
-
-
-
-
Page 299
-
-
-
Let us revert to the state of affairs around the close of the last century (1900), and when the stars were believed to be more or less uniformly distributed through infinite Euclidean space.
-
Okay. Better: through visible space.
-
According to Newton's Law of universal gravitation, the mutual attractions of material bodies should cause the stars to become grouped together into a configuration of uneven density.
-
No. Newton's Law depends very much about initial conditions of positions and velocities.
If you start with the initial condition that the positions of all objects considered are random (within certain boundaries), but all the speeds are zero, then all the objects will move (more or less) towards one point and collide.
-
-
-
Consider a quasi-uniform distribution of stars.
-
Okay. Can such a uniform distribution exist in reality?
-
On a grand macroscopic scale we may view the distribution of one dust particles, packed together densely enough to simulate a continuous cloud of matter.
-
This is a simulation as a thought experiment, but can such a single cloud of matter, in a for the rest empty space really exist?
-
Newton's law, when applied to the interior of a continuous distribution of matter, is expressed by Poisson's equation.
-
Where phi is the Newtonian potential, k the gravitational constant and mu the density of matter.
-
That is true, but how is equation (1) applied in reality? How is mu calculated? Based on observations?
See also: page 267.
At the end of page 299:
-
We conclude therefore that the only possible uniform distribution of matter is one in which there is no matter: and this is another way of saying that a uniform distribution is impossible
-
This raises a philosophical issue. How can you claim something based on equation i.e. equation (1), for which there exist no experimental proof that this equation is correct?
The whole issue is: are there uniform distributions? If the answer is yes than the equation which shows that this is not possible, is wrong.
|
Page 300
-
In view of the incompatibility of Newton's law with the observed uniform distribution of matter, Neumann and Seeliger, in 1896, suggested a slight modification of the law of gravitation, which would have for effect to render a uniform distribution possible.
-
This raises the very important question: Exactly what was observed?
Was a continuous distribution of dust particles observed? I doubt that.
Was a star cluster observed? See: https://en.wikipedia.org/wiki/Star_cluster.
-
The equivalent of Poisson's equation when the Neumann-Seeliger law is used, is
-
| (2) |
grad(phi) - lambda*phi = 4*pi*k*mu |
Where lambda is a positive constant, which may be as small as we choose.
-
-
Let us now turn to Einstein's law of gravitation.
-
Okay
-
We recall that in the general theory, as developed to this point, space-time as a whole was flat, the flatness being departed from only here and there , inside matter and in the proximity of matter, as per Einsteinian law of space-time curvature, or gravitation
-
-
Space-time extended to infinity, and at infinity it was flat, the flatness being departed from only here and there, inside matter and in the proximity of matter, as per Einsteinian law of space-time curvature, or gravitation.
-
Space-time consists of 3 space dimensions and 1 time dimension. Only the 3 space dimensions can extend to infinity. The time dimension not.
The time dimension can only be accounted for from minus infinity to the present. Anyway all of this is tricky.
See also: page 270.
-
-
-
Einstein was averse to the idea that space-time could retain a definite, flat structure at spatial infinity.
-
In classical sense there exists no clear distinction between space and time. Normally we discuss the present and the past. The past started with the Big Bang 13.9 billion years ago.
under construction
|
-
-
-
Einstein observed that not only was the matter of the universe uniformly distributed (on a cosmic scale) but in addition the relative velocities of the stars appeared to be small, so that it was possible to select a frame of reference relative to which the stars would be approximately at rest.
-
What means uniformly compared with non-uniformly?
Within our galaxy you could claim that the stars are uniformly distributed, but within in a scale much larger than our galaxy they are not.
Using that same reasoning you can define a large frame in which the galaxies approximately at rest, but in which the stars are not at rest.
This sentence also raises a philosophical issue.
-
-
-
The problem was therefore to conceive of a space-time universe which would be consistent with a uniform distribution of matter at rest.
-
What is the difference of a space-time universe versus a universe?
-
-
-
-
Page 301
-
The surface of the two-dimensional sphere, and not the volume enclosed within the sphere, is the analogue of the finite space of the universe.
-
It is tricky to compare something local and closed (a sphere) with someting global and open.
See also page page 244
-
-
-
By reason of the characteristics just described, Einstein's universe has been called the Cylindrical Universe
-
-
Now a cylindrical universe filled with matter uniformly distributed, at rest, is incompatible with earlier gravitational equations, viz with the equations
-
-
Okay,
Einstein, however, overcame the difficulty in a manner reminiscent of Seeliger's modification of Newton's law, i.e. by adding to the equations (3) a corrective term involving a new universal constant Lambda.
-
It is easy to add such a term, but very difficult to calculate based on actual observations, because these observations should involve the whole of the universe.
This is specific tricky because generally speaking: the universe at present can not be observed. What we observe at present is the state of the univerese in the past.
-
-
-
-
Einstein therefore, added the term Lamda*gik to his earlier equations, and obtained in place of his original law (3) for space-time curvature inside matter the amended law
-
| (4) |
Gik-0.5*gik*G + Lambda*gik = Tik |
-
Page 303
-
-
-
-
-
-
-
But we must remember that Lambda being equal to the mean density of matter in the universe, is an extremely small magnitude, far too small to be disclosed by measurements over such restricted areas as are available in our solar system.
-
The density of our solar system depents about the radius considered. It is easy to accept that the density of 10*, 100* and 1000* that radius becomes smaller and smaller. At a certain distance stars in our neighbourhood have to be included which will slightly increase this density.
-
-
-
Explorations of space over distances accesible only to larger telescopes would be required.
-
And how would these explorations solve the mystery of Lambda
-
-
Page 304
-
-
-
-
-
De Sitter was of course perfectly well aware that our universe does contain matter, but he assumed that the amount of matter present was too trifling (Wester's: insignificant) to affect the spherical structure otherwise than locally.
-
What did he mean with the last part. What did he mean with: The speherical structure (of what)?
-
-
-
-
-
-
-
-
Page 306
-
To many this dualisme appeared objectionable.
-
The whole situation becomes much simpler if you consider the state of the universe and the evolution of this state from a physical point of view (in time) and forget the mathematics. Specific forget concepts like curvature.
-
-
-
-
-
-
-
-
-
-
-
-
Page 307
-
-
-
-
-
-
-
From these conclusions further important consequences follow; in particular, we must assume that the inertial mass of a body must be generated solely by the mutual actions existing between this body and the other bodies in the universe.
-
What is the reason to use the concept of inertial mass and not mass?
-
-
-
-
-
-
Page 310
-
Futhermore, Mach's idea presented insuperable difficulties, Newton's Law of gravition stated that the attractions exerted between bodies depended solely on their masses and mutual distances ; the conditions of relative motion or rest of the bodies being considered irrelevant.
-
That is too simple. For any practical application of Newton's Law the initial conditions are of uttermost importance. In fact in order to apply Newton's Law you need a sequence of (x,y,z,t) observations at discrete moments.
-
-
-
-
-
-
-
Einstein's gravitational equations without the Lambda term i.e. the equations applying to the infinite universe, namely Gik = 0, had received brilliant support in having enabled him to account for the motion of the planet Mercury, and to anticipate such unsuspected phenomena as the double bending of a ray of light and the Einstein shift-effect.
-
-
-
-
-
Page 311
-
But here integrations of an extremely difficult nature awaited mathematicians
-
An honnest comment.
-
When the equations were treated in a very approximate way, they yielded Newton's law of gravitation and the Einstein shift.
-
More detail is required.
-
When the approximation was increased, they yielded the double bending of a ray of light.
-
More detail is required.
-
When the approximation was increased still further, we obtained the precessional advance of Mercury's perihelion.
-
Why do you study an approximation and not the real equations.
-
When treated in a more general way, they enabled Einstein to predict that gravitation would be propagated with the speed of light.
-
Which specific term in Einstein's equations describes the speed of gravitation?
-
-
-
-
Chapter 34.
34. The Importance of Space-Time, and the Principle of Action - page 319
-
-
-
-
-
But when we represent these intensities in terms of space-time, we find that they are given by the various components of the same space-time tensor Fik; the time components give the electric force while the space time components yield the magnetic force.
-
This requires more detail. Both are intertwined and time dependent.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
At the end of the page:
-
Yet, had men realised that our world was one of four-dimensional Minkowskian space-time, and not separate space and time, things would have been different.
-
under construction
Page 320
-
-
-
Conservation of energy is given by the time component, while conservation of momentum is given by the three space components, of one same space-time tensor law of conservation.
-
Yet also here both are intertwined.
-
All these advantages of space-time appeal very strongly to the theoretical investigator with deals with mathematical equations; but they all go to show how much simpler it is to understand the workings of the universe when we realise that the fundamental continuum of the world is space-time and not separate space and time.
-
The understanding of the working of the universe implies a detailed description of the behaviour of the physical (chemical) processes that take place throughout the entire evolution of the universe.
-
We must now mention another most important conception of classical science, namely, Action; and we shall see that this important mathematical entity finds its place in a perfectly natural way in the world of space-time.
-
The concept of time becomes tricky as we will see in the next sentence.
-
In order to understand the significance of Action let us consider any mechanical system passing from an initial configuration P to a final configuration Q.
-
In this context, as an example, can we consider the solar system as a mechanical system?
Based of what is discussed at page 324 (i.e. the whole world) the answer should be: Yes.
-
Classical science defined the Action "A" of this system as the difference between its total kinetic energy T and its total potential energy V, taken at every instant and then summated over the entire period of time during which the system passed from the initial state P to the final state Q.
-
That is clear. Except how is the initial state P observed i.e. calculated? And how is the final state Q of our solar system observed i.e. calculated?
Page 321
-
-
-
-
-
-
-
Various forms may be given to the principle of Action; here we consider only the form which embodies the concept of Action as defined above; it is called Hamilton's Principle of Stationary Action.
-
Okay
-
-
-
-
Page 323
-
-
-
-
-
-
-
There is now perfect symmetry between the roles of space and time.
-
This requires a definition of the word symmetry. Normally symmetry is used within one dimension i.e. between the left and the right side in the same (x or y) direction. In this case the comparison is between two incompatible dimensions.
-
Now there was still another aspect of the principle of action which was extremely displeasing in classical science: By making the present course of a phenomenon contingent on a condition which could be determined only at some future date, it acquired a teleological character.
-
What is the meaning of the word: teleological character?
Accordingly to Webster: The fact of being directed toward an end or shaped by a purpose or by the design of a divine Providence as opposed to purely mechanical determinism or causation.
-
But as Planck points out, with the action as given by an energy in a volume of space-time, we may, by placing space and time on the same footing, regard duration as static; and the unsatisfactory teleological aspect of the principle may be obviated
-
What Planck points out is not clear. For example: what means static in this context.
As such it can not be used to eliminate a different explanation.
-
-
-
Assuming the world to be built up of electricity and metrical field the possibility of obtaining the "function of action" L of the universe would seem to be within our grasp
-
I expect that L is a function of t, valid from the beginning of the Universe until the present.
This sounds interesting however impossible to be realistic.
At the end of the page:
-
Could this result be accomplished, a momentous discovery would have been made, since all the laws of the physical world would be comprised in the expression
-
delta Integral (Ldw) = 0
-
This sounds like wishful thinking.
Page 324
-
Unfortunate we are far from being able to determine the "function of action" of the universe, for there may be physical elements entering in its constitution whose nature we as yet ignore.
-
Then why discussing this issue, when it is full of speculation?
-
(Furthermore, we might mention that the very validity of the principle of action is called into question by the quantum phenomena)
-
Quantum theory has a broad spectrum. More detail is required about the details of this remark.
-
-
-
We are, of course, then concerned in discovering the only existing world, the real world for us.
-
Okay.
-
-
-
Physics, this time as physics of fields, is again pursuing the object of reducing the totality of natural phenomena to a single physical law: it was believed that this goal was almost within reach once before when Newton's Principia, founded on the physics of mechanical point-masses, was celebrating its triumphs.
-
And still does.
Chapter 35.
35. The Mystery of Matter - page 327
-
One of the greatest merits of the theory of relativity has been to allow us to represent gravitation as a direct consequence of the curvature of space-time.
-
That sounds very promising in theory but very difficult in practice. Any recipe how to do that is completely lacking.
-
We remember that in the course of our wanderings we came across two foreign tensors: Tik, the matter tensor and Eik, the electromagnetic tensor.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Chapter 36.
36. The Theories of Weyl and Eddington - page 330
-
-
-
-
-
In order to understand Weyl's theory, which may be regarded as a generalisation of Einstein's, it will be necessary to enquire into the nature of Weyl's geometrical contributions.
-
Okay.
-
-
-
-
-
-
-
Now it is possible to remove this restriction imposed by Riemann without falling into any logical inconsistency; and we may perfectly well assume that the two unit rods which coincide at a point A may cease to coincide when brought together at another point B, provided they have followed different routes while moving from A to B.
-
The assumption is: that this is a physical fact and that it is permanent.
-
From a purely mathematical angle, such an assumption is by no means absurd; and it is this generalisation of the possible behaviour of our conceptual measuring rods which was studied by Weyl.
-
This is not pure mathematics. When you move a rod from A to B this is a physical process.
When you move two identical rods from A to B, along to different routes, and in one case the lengths stays the say and in a second case the lengths become different, you want to know why.
Is this because of the specific rods used or in the routes followed?
-
-
-
-
-
-
-
-
Page 331
-
We are merely speculating, as mathematicians, on a logical extension of geometry.
-
That is the question. The above case is based on one assumption. That means it more or less becomes a thought experiment.
-
Obviously, if this is the case, the statement that two lengths situated at different points A and B of space are equal in magnitude is necessarily indeterminate.
-
That is correct, specific if this can be established by a real experiment.
-
The two lengths might measure out as equal if we displaced our unit rod from A to B along a certain path, and as unequal if we displaced our unit rod along some other path.
-
What happens if we move, for example, 10 unit rods along different paths from A to B?
In principle, now it is possible that all the unit rods are different in length.
If that is the case 'length of a unit rod' is completely indeterminate.
-
We therefore agree to consider that at every point in space there is a fixed rod which is to serve as unit of length when we measure lengths situated by its side.
-
In principle this is possible, but if result of the previous experiment is correct (with the 10 unit rods) then this does not make much sense.
-
Owing to the difference in routes followed by the two rods, one having remained fixed and the other been made to describe, the two rods will no longer coincide when we place them side by side after the completion of the circuit.
-
This exercise only makes sense if you repeat exactly the same experiment with two unit rods B and C and the end of the circuit both B and c are equal to each other and both unequal to A.
-
Consider a curved surface in three dimensional space.
-
Okay.
-
If at this point A two short rods applied to the surface coincide in direction and if, while one rod remains fixed, the other is displaced from A along the curve in such a way that for each successive infinitesimal displacement the rod remains in the same direction, it would be erroneous to suppose that when the second rod had been returned to its starting point its direction would still coincide with that of the first rod.
-
The first question to answer is if a second person repeats the same experiment will the final result be the same?
The answer is important because exactly how is the rod moved over this closed curve. Specific, how do you take care, that the direction of the rod remains the same?
For example if the closed curve is the equator of a sphere the direction is never the same.
At the end of the page 331:
-
A distinct discrepancy would be found to exist between the directions of the two rods, and the size of this discrepancy would depend on the area and the location of the closed curve which the second rod had made to follow over the surface.
-
-
-
Page 332
-
If we had operated on a plane sheet of paper instead of on a curved surface, the discrepancy would not have arisen, since a plane surface has no curvature.
-
The problem is the influence (or behaviour) of a curved surface. If you remove the curved surface there is no problem. Is that what we want?
-
-
-
-
-
-
-
-
-
-
Page 335
-
-
-
Thus, two identical electrons situated, first, at any one point then separated, would in general differ in size and in charge when brought together again.
-
How do you know that at the beginning of the experiment both electrons are identical and at the end of the experiment are different?
Of course a certain theory can claim that this is the case under certain conditions, but if the initial state and the final state cannot be properly tested what is the point i.e. the value of the theory?
-
-
-
-
-
Now, all these anticipations of Weyl's theory in its original form are in conflict with precise observation.
-
If that is a fact than in casu what is the importance of Weyl's theory?
-
-
-
-
-
-
-
-
-
-
-
-
Chapter 37.
The Methodology of Science - page 343
-
An opinion commonly expressed by philosophers is that the function of physicists should be to weigh, measure, tabulate, and discover new chemical elements, new facts; and the aim of mathematicians, to solve equations.
-
The function of physicists is not so much to solve (calculate) numerical equations (with the aid of mathematicians), but more to test the results.
-
etc,, but that when he proceeds to discuss the implications of his discoveries and to draw conclusions on the subject of space, time, energy, laws of nature, he is getting beyond his depth and encroaching on the field of the metaphysician.
-
It is the task of the philosophers to investigate if the logic used by the physicists is accordingly to common standards.
-
-
-
-
-
-
-
-
-
-
Page 344
-
-
-
Yet they are not, properly speaking, great mathematicians.
-
It is one of the great philosophical questions if the laws of nature require (in order to describe) complex mathematics. The laws of nature describe physical processes which in fact are chemical processes, as such they cannot that be complex, except to predict them accurately in due time, which in many cases is impossible. One specific case are explosions i.e. supernova's.
From a mathematical point of view the question is, for example: if the laws of nature require complex numbers.
-
-
-
-
-
-
-
-
Page 372
-
-
-
-
-
-
-
It may happen that further experiment will enable us to determine which of the various hypotheses corresponds to concrete reality.
-
I would write:
It may happen that the difference between the actual and predicted results of further experiments will help us to decide which of the underlying theories the best are.
-
-
-
-
Page 373
-
-
-
-
-
-
-
-
-
Furthermore, even if this view were contested, there would seem to be no reason to suppose that nature should prefer simplicity to complexity in the first place.
-
Nature (the laws of nature) does not prefer anything. We can predict the positions of the planets based on certain initial conditions, but we cannot predict the actual initial conditions.
-
-
Page 374
-
-
-
From this it follows that it is at least
-
-
-
-
-
-
-
-
-
Page 375
-
-
-
-
-
However, it cannot be emphasized too strongly that from a practical standpoint these questions are purely of academic interest.
-
? I would say philosophical interest.
-
The physicist and the mathematical physicist are compelled to operate and reason as though they believed in the real existence of a real absolute objective universe, one of space and time, according to classical science ; one of space-time according to the theory of relativity.
-
The question is if the meaning of the word existence related to the two concepts: space and time versus space-time is the same.
-
In fact, as we have said, were it impossible to conceive of a common objective world, one existing independently of the observer who discovers it bit by bit, physical science would be impossible.
-
This is a tricky sentence. In order to unravel the laws of nature you need human beings, but the laws of nature it self are objective and independent of humans.
-
-
Page 381
-
-
-
-
-
-
-
-
-
It is the same with a number of electrical problems of widespread industrial importance; likewise, with Einstein's law of gravitation, the orbits of the planets cannot be calculated unless we appeal to elliptical functions
-
The orbits of the planets can not be calculated accurately by analytical functions (including elliptic functions). The only way is by numerical methods, for example the Runge Kutta method is a way to solve ordinary differential equations.
The special branch which studies solutions of GR is Numerical Relativity. See https://en.wikipedia.org/wiki/Numerical_relativity
-
-
Page 382
-
-
-
Here we must recall that however mysterious it may seem, nature appears to be amenable to mathematical investigation and to be governed by rigid mathematical laws, at least to a first approximation.
-
Nature is governed by physical laws which can (partly be) described by using mathematics including parameters.
-
-
-
-
-
-
-
-
Page 383
-
Then again, nature must be simple, or at least simple to a first approximation.
-
This sentence has no scientific 'value'. What means simple?
-
Theoretically, simplicity cannot exist in nature, since the whole influences the part and the part influences the whole.
-
The problem when studying the universe is that all objects influence each other. This implies (more or less) that it is a complex problem and it is not simple. The philosophical issue what is allowed to make it simpler?
One problem is that physical clocks (using light signals to operate) are also objects part of these same influences. This raises the question if it is allowed to consider a universe without physical clocks. If it is allowed to consider a universe which contains clocks which all run simultaneous.
See also: Reflection III - The philosophy of Science. Experiments and Postulates.
-
It is because in meteorology this restriction of active influences to a minimum appears impossible that long-range weather prediction is any man's guess.
-
To be able to predict something implies that what you want to predict should be stable, which in turn implies there should be very little possibilities to influence.
One of the reasons why weather prediction is so difficult (and unstable) is because of the long (time) delays in cause and effect.
-
-
-
-
-
-
Page 404
-
-
-
-
-
A case in point would be afforded by a comparison of Einstein's and Newton's co-ordination of gravitation and mechanics.
-
Okay
-
If we are concerned solely with the facts of planetary motion and mechanics known to Newton, then Newton's laws of mechanics and his law of gravitation are by far the simpler.
-
First of all, Newton's law is simple but very useful and maybe more practical than Einstein's.
Secondly, Newton's law is not accurate enough to explain the trajectory of the planet Mercury, because it is based on the assumption that gravitation acts instantaneous, which is not the case. Einstein's Law is more general but also much more complex. This comes with a high price. Maybe the price is too high.
-
But if we supplement the facts known to him with those more recently discovered, Einstein's synthesis has the advantage, for Newton's co-ordination would necessitate a number of additional hypotheses ad hoc.
-
This sentence requires a more detailed explanation.
What is the advantage of Einstein's synthesis? What are the additional hypotheses?
-
-
-
-
-
It may happen, of course, that the simpler synthesis will conflict with certain philosophical prejudices, but objections of this sort will always give way eventually before the higher criterion of simplicity.
-
The whole issue of simplicity is a philosophical issue. When is simplicity a valid argument and when not.
The LHC is a very complex tool to perform certain experiments, but if you want understand to certain physical processes it is a must.
-
Indeed, we know that men finally accepted Galileo's stand.
-
Galileo's stand is based on a simple and uniform world view. This view is generally summarised as: that a large object can be surrounded by a swarm of smaller objects, which each can be surrounded by even smaller objects.
That means in Galileo's case simplicity wins, in Einstein's case complexity wins.
Under construction
-
If, then, we may assume that the criterion of simplicity presents no further difficulty, the problem reduces to determining whether or not the theoretical physicist introduces presuppositions and assumptions uncritically.
-
I clearly doubt if the last word 'uncritically' is true.
-
-
-
Page 405
-
The purpose of science is, as we have said, to co-ordinate facts and to obtain thereby a common knowledge which will hold for all men.
-
The purpose of science is to collect and combine facts and to understand the relations between almost identical facts and what the causes of differences are. The second step is by means of experiments to understand all these processes in more detail.
-
But our co-ordinations, deductions and inductions must be conducted accordingly to rigid rules which all men will recognise.
-
Science should be performed conforming to accepted rules.
-
-
-
We shall assume that the rules of logical reasoning will serve our purpose in this respect.
-
The most important issue is: what exactly are 'the rules of logical reasoning', science is supposed to follow?
-
-
-
Let us consider now what scientist mean by uniformity of nature
-
Okay.
-
It may mean that nature is regulated by universal laws.
-
This sentence requires the definition of two words: 'regulated' and 'universal laws'?
Both words require a clear definition; otherwise the sentence can not be evaluated as either right or wrong.
The rules, discussed above, should clarify this issue.
-
In this form, it is, obviously not a presupposition adopted uncritically.
-
Also here a definition of the word 'presupposition' is required.
The issue is that we should be able to question and to criticize science.
-
If the modern physicist accepts this uniformity it is because it has been confirmed a posteriori in so large number of cases that it seems simpler to accept it than to reject it, at least until further notice.
-
How can you confirm to something when the concept uniformity is not clear.
In this paragraph 'uniformity of nature' is defined as processes regulated by universal laws, but in this context both the words 'regulated' and 'universal laws' are not clear.
-
-
-
-
-
-
-
Nature may not be rational and our logic may be unable to cope with it.
-
We can not claim that nature is either rational or irrational. The evolution of all physical processes is what it is and we humans have to accept that.
-
If this be the case, statistical knowledge may be the only type possible, though even statistical knowledge may fail us.
-
Statistical knowledge is result of (almost) identical experiments performed 1000 times. The point is that the results of experiments are not always the same. For example we can get 498 times A, 497 times B and 5 times C. We can discard the results C. The question now is: Why do we get 50% A and 50% B?
-
-
-
-
-
-
-
-
Page 406
-
-
-
As a matter of fact, even were we assured that the uniformity of nature was a mistaken belief; we should continue to be governed by it just the same?
-
This sentence should be clearly answered: NO. The sentence is not clear because the concept 'uniformity of nature' is not clear.
Nature is neither uniform nor non-uniform. Certain processes in nature are similar and these processes can be described by physical laws, even by mathematics. However the reverse is not true. The laws don't control the physical processes.
The laws themselves are not part of the physical world; they are not part of the evolution of the physical world.
-
-
-
-
-
-
-
-
Page 407
-
-
-
We might also mention the Principle of continuity and the principle of causality as understood by modern physics.
-
Okay.
-
The Principle of continuity implies the eradication of all action at a distance such as is exemplified in Newton's law of gravitation.
-
You can only understand this sentence if you mean what Principle of continuity means.
Newton's law assumes that gravity acts instantaneous. La Place did not assume that. This has nothing to do with the Principle of continuity, except if that is what it means,
-
-
-
-
-
-
-
Only when as a result of Maxwell's discoveries, electromagnetic induction was found to be propagated by continuous action through a medium, did the popularity of the principle increase.
-
This is not a medium in the physical, material sense?
-
This leads us to fields physics, to the discovery of a new category differing from matter, namely, the elctromagnetic field.
-
The electromagnetic field itself is no physics. Electromagnetic radiation is physics. The field is mathematics.
-
-
-
-
Page 434
-
-
-
-
-
However, before following Einstein in his solution, we may state that Poincaré, as far back as 1906, had succeeded in establishing a most important point
-
Okay
-
Prior to his investigations it had been held that Newton's law of gravitation constituted a powerful argument against space-time theory
-
Okay.
-
For, on Laplace's authority, it was believed that the observed planetary motions required that gravitation should be propagated with a speed many times greater than that of light; a fact difficult to reconcile with the maximum velocity c required by relativity.
-
Something must be wrong when the speed of gravitation is larger than the speed of light?
-
Poincaré, however, proved that the force of gravitation could perfectly well be propagated with the speed of light and yet yield laws of planetary motions practically identical with those of Kepler.
-
This requires a detailed comparison with Laplace's idea versus Poincaré's idea.
-
He proceeded to consider the various possible laws of gravitation compatible with the flat space-time theory though reducing to Newton's Law for slow velocities.
-
Okay.
-
-
-
-
-
-
-
-
-
-
Page 437
-
-
-
-
-
We may condense it into the statement that where there is action there must also be a reaction.
-
This requires the definition of 'action' and 'reaction'
-
Now, in rigidly flat space-time, the courses of free bodies must be conceived of as directed by the geometry or structure of space-time.
-
This sentence raises more questions then it solves.
-
Hence there exists an action of the space-time structure on the bodies.
-
-
-
Page 439
-
-
-
-
-
Today the cylindrical universe is a discarded theory, having been superseded by Lemaitre's expanding universe.
-
-
-
-
-
-
-
Chapter 38.
The General Significance of the Theory of Relativity - page 443
-
The most interesting aspect of the entire theory for philosophers would appear to be the discovery of space-time, with the paradoxes of feeling to which it leads.
-
This is of much more interest to physicist as to philosophers.
For philosophers the use of the concept space-time is of interest because it is mathematics and not physics.
-
Thus the duration of our life, the distance we cover, have no absolute significance.
-
Here for a philosopher it is interesting what means physically: 'distance we cover'.
-
Two twins might both live seventy years in their own estimation and yet if they met again before their death one might be younger than the other.
-
This sentence is not clear. One improved version is:
-
Two twins might both live seventy years in their own estimation and yet if they meet at the dead bed of the stay the travelling twin is still alive and the stay at home twin is already dead for 100 years.
A more mathematical description is:
-
Two twins travel and yet when they meet the clock of the travelling twin has advanced 70 years and the clock of stay at home twin 170 years.
The most important physical question is: On average is the moving twin still alive?
Is the physical aging of his whole body thoroughly uniformly retarded as his clock readings seem to indicate?
I doubt that. To answer this question it should be assumed that both twins stayed during the whole test inside the rocket. The main difference is that one rocket stayed on the platform and the other moved through space.
-
Two man starting from the same point and travelling in the same direction might both cover what they would measure as the same distance, and yet might find when they came to a stop that they were many miles apart.
-
This sentence is wrong. The issue is in the definition of words measured and calculated.
What is measured in the text is the distance covered in space-time. However this distance is not measured but calculated. This is the value mentioned as ds^2.
What is measured are the times dt and the distances dx,dy and dz as mentioned in the equation to calculate ds^2.
See: page 195 and also: page 199
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Page 447
-
-
-
-
-
In the case of space-time, this would imply that the distance between any two point-events should exhibit the same space-time separation holding for all observers regardless of their motion.
-
This implies a uniform cookbook how this space-time separation is calculated based on observations.
-
Now, in the space and time of classical science, no such invariant space and time distance was possible.
-
That may be true, but the issue remains what are the true benefits.
-
A simple example may make this point clear.
-
What you need is a clear example.
Unfortunate the example does not give enough detail.
-
Suppose that in classical science we are standing on a railroad embankment, and viewing the production of two instantaneous events - say, two light flashes emitted by two spatially separated signals on the line.
-
Okay. The issue is: are the two flashes approach us from the same direction or from opposite direction? I expect the last.
An other issue is: are the two flashes emitted simultaneous? Again I expect not.
-
By taking into consideration the speed with which the light signals had progressed towards us and by measuring our distance from the respective signals, we could determine the spatial distance between the two distances from the respective times at which the flashes had occurred.
-
This is tricky because the speed of light is a physical issue and you need very accurate clocks and large distances.
- In case we observe both flashes simultaneous and the distance is the same, that is no guarantee that both flashes were emitted simultaneous.
- In case the two signals are not received simultaneous and the distances are in different directions, the speed of light has to be taken into account in each direction, in order to calculate the respective emission times.
GR makes this easy by claiming that the speed of light is the same.
-
We should thus obtain the temporal separation and the spatial separation between the two events as referred to the embankment.
-
This should be: as referred to the reference frame of the embankment.
-
But suppose now that we had viewed the same two events from a train moving uniformly along the track.
-
And what is then observed in detail?
-
Suppose that the observer on the platform observes the two flashes simultaneous at point X at time t (indicated at a clock at point X)
If the observer at the train is exactly at point X at time t he will also observe the two flashes simultaneous.
- If the observer on the platform does not observe the two flashes simultaneous, what the observer on the train sees changes. There is a chance that he sees the two flashes simultaneous, but most probably not.
-
In classical science, time being absolute, the temporal separation between the two events would, of course suffer no modification.
-
That depends how this temporal separation is measured with clocks.
- When the times on the train are measured with clocks on the platform there is physical no difference so the times should be the same.
- When the times on the train are measured with clocks on the train there is physical difference so the times should be different
In reality this is a very tricky experiment.
-
The spatial separation as referred to the train would, however, generally be different.
-
In agreement with what is predicted.
-
We can understand this by supposing that the train passed before the two successive signals as their respective flashes were emitted; in this case, as referred to the train, the two events would have occurred at the same point of the train, and so their spatial separation would be zero.
-
This is a tricky explanation.
-
Now, what Einstein tells us is that had we performed our measurements with extreme accuracy, using our customary chronometers and rigid rods, we should have found that the time separation between the two events had varied slightly; and that as a result this slight variation would have cancelled the corresponding change of the space separation, leaving the space-time distance unmodified.
-
This all requires that you need a good cookbook which explains how the measurements are performed.
-
Calling x and t and x' and t' the space and time separations, as measured from the embankment and the train, respectively, we would have found that
-
x^2 - c^2*t^2 = x'^2 - c^2*t'^2
-
x and x' are really distance parameters.
This equation indicates that this simple example is as simple as it sounds.
-
-
Page 448
-
It is the fact that our measurements would have verified the invariance of this distance, which permits us to consider space and time as amalgamated.
-
This is important.
-
-
-
-
-
-
-
-
-
-
Page 449
-
The great difference between our present views and those of classical science is that whereas in classical science our lines of time-reckoning and of space reckoning were unique, they now offer an indefinite number of possible alternatives, because of the plurality of time and space directions present in space-time.
-
And how does that help me to improve to calculate the trajectories of all the planets around the sun?
-
-
-
The strange results and concepts which the theory of relativity has disclosed have appealed by a number of writers in order to justify an ultra-idealistic philosophy of nature.
-
What means the word: ultra-idealistic?
The only things that the philosophers of science should discuss are the logic underlying the rules, the concepts and the definitions used by both Einstein and Newton.
See also: Reflection 4 - absolute versus relative in Newton (Classical) versus Einstein.
-
-
-
-
-
-
Page 451
-
-
-
-
-
As a matter of fact, this statement is incorrect, for the velocity of light is invariant only for Galilean observers; it is variable from place to place when accelerated observers are considered, and it is also variable in the neighbourhood of matter.
-
IMO the speed of light has nothing to do with respect to the observers. That does not mean that it is not more difficult to measure the speed of when measuring involves accelerations. That the speed of light is not constant when matter is involved is something physical and the same when space is not a vacuum.
-
-
-
In this experiment, we are therefore dealing with a coincidence, with waves of light with pass the same point at the same time.
-
This is in some sense also the problem. The question is, if Michelson's experiment says something about the speed of light (being the same in all directions) or the wave length (i.e. frequency).
-
-
-
-
-
-
-
-
Page 454
-
-
-
-
-
Now, in this interpretation of space-time, there is no room for free will, since everything is already predetermined and pre-exists in the future.
-
The concept of no free will requires a certain amount of absoluteness. The idea that we can describe the state of all the objects from large to small at all levels of detail with a certain type of absolute accuracy. But also we have to know the laws that describe the movements of all these objects with absolute accuracy. That means the movements of all the atoms in a human. Such accuracy is complete impossible.
-
-
-
-
-
-
-
-
Page 455
-
-
-
-
-
-
-
-
-
The next most important aspect of the theory of relativity to consider relates to our conception of real space.
-
The issue is why. My understanding is that in order to understand the reality and to predict the future you must have a clear picture of what is the reality. That means what are the objects and how are they internal operating and in relation to each other. That means the objects comes first and space comes second.
-
We remember that the geometrical space of mathematics was amorphous.
-
See also page 47
-
It possessed no intrinsic metrics, no special geometry, no size, no shape; and the geometry which the mathematician credited to space was purely a matter of choice.
-
The concept of space makes only physical sense. When we use the word space it always is in relation with physical distances.
Geometry in mathematical sense has to do with the shape of surfaces i.e. the surfaces of objects.
-
On the other hand, the real space of physics appeared to posses a definite metrics.
-
Metrics become an issue when objects, mass is concerned.
The question is also here what is the definition of the concept 'real space'?
-
Furthermore, the amorphous nature of space was belied by the existence of centrifugal forces and the like, proving that not all motions through space were equivalent.
-
Is the issue here: mathematical space, physical space or real space?
-
When it became to determining the precise geometry of real space, various methods could be considered.
-
The question arises: What (How) is the deciding moment that we know the precise geometry.
-
-
-
-
-
A still more general method consisted in appealing to the laws of physics in general, and determining the type of geometry which would have to be credited to space in order to permit us to co-ordinate natural phenomena with the maximum of simplicity.
-
To understand this sentence (and in order to use this method) you must know what 'the laws of physics' are, what they imply to solve and not by raising other complex issues.
Why mentioning the concept: 'maximum of simplicity'? Why not mentioning: 'maximum of accuracy'
-
-
-
-
-
-
-
-
Page 463
-
-
-
-
-
The theory of relativity has taught us that, strangely enough, there is nothing in the world of physics to justify our natural belief in the separateness of space and time.
-
"My" natural belief in my existence is that all what exists, exists in space and time. That both means both are closely linked. This becomes more apparent when a clock is concerned, which exists in space and time and which indicates time.
-
It is this discovery, entailing that of the four-dimensional world of space-time, that constitutes the most important contribution of the theory to our knowledge of the universe.
-
The problem is that the time dimension is not physical the same as the 3 space dimensions. Part of the problem is that the time dimension is measured by a clock which behaviour is dynamic, specific as a function of speed and accelerations.
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Appendix - The space and time graphs - page 467
-
-
-
-
-
-
-
-
-
-
-
-
Page 469
-
-
-
-
-
-
-
With the particular units we have chosen, the word-lines of bodies moving along the embankment at a speed of 186,000 miles a second will posses a slant 45 degrees with respect to both space and time axis.
-
That is mathematical 100% correct. The question is: is this also physical correct, because this implies that the speed of light in both directions is the same.
IMO Newton would remark that this is only correct in one particular frame; in a frame that encompasses the total Universe.
-
In other words, the world-lines of such bodies, hence also of rays of light, will be inclined equally to our space and time axis.
-
Okay.
-
-
-
Page 470
-
-
-
-
Thus far, we have been considering happenings with reference to an observer at rest on the embankment, and everything we have said applies in an identical way to classical science and to relativity.
-
In classical science the observer can be considered at rest on the embankment, but the embankment is not considered at rest, as such the speed of light is not considered for any observer to be the same in both directions and the world-lines of the light cones are not symmetrical.
-
-
-
-
-
Now classical science, both as the result of crude experience and, later, of more refined measurements, held to the view that duration and distances were absolutes, in that their magnitudes would never be modified by our circumstances of motion.
-
That complete depends how duration is measured. In order to measure duration you need a clock and if the behaviour of the clock changes as a function of motion than also duration changes.
Classical science was aware of this problem, and that is why they tried to make clocks as accurate as possible, in order to measure speed and distance.
-
Accordingly, regardless of whether we were at rest on the embankment or in motion, the duration separating two events or the distance between two fixed points on the embankment was assumed to remain the same.
-
-
-
-
-
-
-
-
-
Page 472
-
-
-
-
-
-
-
In classical science, space was regarded as a three-dimensional continuum of points, because it was possible to localise the position of a point in our frame by referring to its three co-ordinates.
-
That is the definition of mathematical space. Added to this definition should be that mathematical space is completely empty.
The definition of physical space is the same as mathematical space, except it exists in time and is not empty. Physical space contains matter, objects and these objects exist in time.
Time has to be considered, as part of physical space and as such defines a continuum.
To measure time we use a clock. The inner workings of a clock are based on light signals. Time in principle is indicated by ticks or counts. The larger a clock the slower the number of counts. What also influences the counts is the speed of a clock. A clock at rest counts the fastest (using light signals).
Newton's involvement of handling physical space is based on calculation (or measuring) the position of all objects at a particular instant of time.
Einstein's way seems to be completely different, but in reality if you want to calculate (or measure) the positions of the same objects, the technical complications are the same or much more complicated.
-
Suppose, then, that he wished to measure the distance between two points in space.
-
The first question to answer is:
(A) Are this two points on the surface on the same object or (B) on two objects?
If the answer is A then the second question is: Is the distance measured simultaneous or not.
To get an idea how difficult it is to measure the distance between two points on the surface of the earth select this link:
VB train operation . The program demonstrates the distance between a train and one observer.
At the end of page 472
-
All we have to do would be to stretch a tape between the two points, and the length of the tape would define the distance between them.
-
This is only possible if we want to measure the distance between two points on the surface of the earth simultaneous.
In that case the centre of the earth is considered fixed and the rotation of the earth is not taken into account.
In all other cases to measure the distance between two points is much more complicated, because the distance changes continuously.
-
-
-
-
Page 473
-
-
-
Here again, we might claim that space and time constituted a four dimensional continuum of events; for we could always localise the occurrence of an instantaneous event by measuring three spatial co-ordinates in our frame of reference, and by computing the instant at which the event occurred.
-
We can not speak about 3-dimensional-space and time as if this are two separate entities. Physical space and time are irremovable linked to each other.
To measure the distant of an event in space, relative from my position i.e. my reference frame, is always tricky, except if there exist a physical link i.e. a grid.
To measure the time of the event is even more tricky except if the clocks in use are physical linked to the grid.
-
But suppose we wished to measure the distance between two events occurring, say, one in New York on Monday, and the other in Washington on Tuesday.
-
This immediately creates a problem: How is the time measured at two different locations?
The physical distance in space can be measured if we use a physical grid with clocks linked to the grid.
-
Obviously the problem would be meaningless.
-
Why do 'you' raise this problem (question) when the problem (question) is meaningless?
In principle this is exactly the same problem as discussed at page 447. There are two events happening at different positions in 3D space.
-
We might say that the distance in space between the two events was so many miles, and their distance in time so many hours; but we would be unable to measure the distance in space-cum-time directly, whereas, with the aid of the tape, in our previous example, we were able to measure immediately the spatial distance between the two points.
-
The problem with this example is that the point 'New York' and the point 'Washington' define a rotating reference frame, which moves as a type of Merry go round through space. In practise this is the frame of our solar system. Within that frame the positions of both events can be marked and the distances calculated.
It does not make sense to differentiate between the two concepts 'distance in space' and 'distance in time' of the two events, because time is not something physical. In stead of 'distance in time' it is better to speak about 'difference in time' or a duration.
-
-
-
-
-
Consider, as before, the embankment, an observer at rest at O (whose word-line is Ot), an observer in motion (whose word-line is OD), and finally two point-events A and B (Fig XV).
-
The problem is you can easily make such a drawing on a piece of paper, but how do you draw such a drawing based on the reality? How do you draw the point-events b't and a't based on actual observations?
-
-
-
-
-
-
-
-
Page 474
-
-
-
Now, and only now, thanks to ultra-precise experiment and the genius of Einstein and Minkowski, is there any advantage in speaking of space-cum-time as a four dimensional continuum of events which we call space-time.
-
The problem is that space-time is not something that exists. It is a method to make the movement of objects better visible in time. This is specific the case when objects move a long a straight line (1D) or in a flat plane (2D). This becomes very difficult when objects move in 3D.
-
-
-
Prior to these achievements, the concept of space-time was as artificial as that of an n-dimensional continuum of space, time, pressure, temperature, colour, etc.
-
Space-time is still something artificial. The first problem is that it is a mathematical issue and not a physical concept. The second problem is that the concept in order to use, and to demonstrate that it is correct, requires observations. This is exactly the same problem as when you want to use any law.
-
We shall now investigate in what measure the graphical representation of classical science will have to be modified in order to harmonise with the empirical facts revealed by ultra-refined experiment.
-
Empirical facts are facts based on observations and experiments alone. See Webster. To investigate these facts it is important to have a clear description what these ultra-refined experiments are and what the results are.
-
There is no need to modify our understanding of point-events and world-lines; these will remain undisturbed.
-
As long as both concepts have nothing to do with these ultra refined experiments.
Both this line and the previous line raise a philosophical issue.
-
-
-
-
-
The bifurcation between the two graphs arises when we consider the principle of the invariant velocity of light.
-
-
-
-
-
-
-
-
The physical significance of this fact was that the velocity of light for the moving observer would be less than for
the embankment observer.
-
This is tricky. The whole issue is that from a physical point of view the speed of light of an explosion happening just above the surface of the earth should be the same in both directions, centred about the point of the explosion.
The physical issue is also, that this point does not coincide with the point where the explosion happened at the surface of the earth.
-
Now this result contradicted the principle of the invariant velocity of light
-
This leads two conclusions: either the previous reasoning is wrong (which resulted in what is called: this result) or the concept invariant of light, is wrong. Also both can be wrong).
-
-
Page 475
-
Hence we conclude that space and time directions Ox and Ot are no longer absolute; every observer will have to measure time along his world-line and space along a line orthogonal to this world-line.
-
The problem is that general speaking the clock of every observer behaves physical different. This behaviour becomes rather easy to predict when the clocks move in a straight line away from each other. This behaviour becomes more complex when more rotation is involved.
The same
-
It follows that there exist an indefinite number of time directions given by the world-lines of the various observers, and correspondingly indefinite number of space dimensions.
-
What makes this so complex is that the time directions of each observer, compared with the other observers, assuming that each observer is situated on a freely moving object, constantly changes in direction, like the world of each observer.
-
A first consequence of this novelty is that simultaneity can no longer be absolute.
-
This requires a clear definition of what simultaneity is, i.e. relative simultaneity versus absolute simultaneity.
-
For whereas, in the classical graph, all events on the same horizontal or space direction were simultaneous for all observers, we now realise that with this variation in space directions , or lines of simultaneous occurrence, the absoluteness of simultaneity must vanish.
-
Every concept must make a distinction. The concept that certain events are simultaneous only makes sense if there are events which are not simultaneous. In order to explain such a claim it must be unambiguous how events are observed or measured. As part of concept it should be mentioned if the same events can be both simultaneous and not simultaneous.
-
For instance, all the point-events lying on Qx' which are there simultaneous with the time zero for the moving observer, appear to be unfolding them selves in succession for the stationary observer.
-
Here you get the philosophical question, how important is this issue for the evolution of the universe, which evolves completely independent for any observer.
-
-
-
-
Page 477
-
-
-
-
-
-
-
If we consider all the observers situated at a definite point at some definite time, that is to say, all observers whose spatio-temporal position is given by the same common point-event, then, regardless of their relative motions, the same instantaneous light-cone holds for all.
-
That is physical correct, because physical there is only one single event and one sphere, which grows in size, centred on the single event.
-
-
-
-
-
-
-
-
-
-
-
-
Page 480
-
-
-
We might, as a final example, consider the trip to the star.
-
In real both the observer at O (on earth) and the star (with observer P) are moving through space in time during the whole trip. This makes this whole example very complicated.
-
if Aa denotes the world-line of the star and OBC the world-line of the travelling twin, we see that he will have lived a time OB+BC during his trip.
-
It is assumed that OC is the world-line of the stay at home twin.
In real the distance between the Earth and the star, during the trip continuously changes and can increase (on average). This makes the exercise complicated.
-
His brother remaining on earth will have OC for world-line. Hence, he will have lived a time OC.
-
Time and age are two different concepts. Age depends about the number of cycles, ticks of a clock.
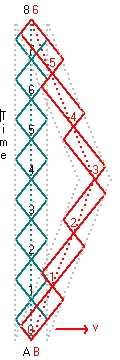
|
-
Ax before, though OB+BC appears larger than OC, it is in reality, shorter , as can be understood by referring to Fig XIX
-
The reason is because a clock at rest ticks faster than a moving clock.
As said above, Age depends about the number of cycles, ticks of a clock.
How larger a clock, how longer the time between each tick, the slower the clock ticks?
The same is depicted on the clock on the left. The clock at rest shows 8 ticks. The moving clock, moving forward and backward along a straight line, only shows 6 ticks.
See also: BookReview "Spacetime Physics" Reflection 3 - Worldline Perpendicular Mirrors - Twin Paradox
|
-
Incidentally, we see how the absolute nature of acceleration causes the traveller's word-line to bend; and it is this absolute bend in the world-line which differentiates the life-histories of the two twins and which is responsible for an absolute, non-reciprocal difference in their respective aging.
-
In the real experiment there are three phases where a change in speed and acceleration is involved:
- At the beginning of the experiment when the speed changes from v=0 to v=Sgrt(vx^2+vy^2+vz^2) or v>0
- Half way of the experiment when the speed changes from V>0 into v<0
- At the end of the experiment when the speed changes from v<0 into v=0
Immediate after the first change in speed the moving clocks started to run behind, with a clock (assumed to be) at rest.
-
-
-
In as much as our choice of units is entirely arbitrary, we might lead to believe that the graph could not depict reality.
-
The problem with the graph of Fig XXI is that the situation in real is much more complex. The issue is not so much the units.
-
-
-
-
Page 481
-
-
-
Here we are living in a world which, theoretically at least, is vastly different from the world of separate space and time, and yet it is only thanks to the ultra-refined experiment and the genius of Einstein and Minkowski that we have finally realised it to be a four-dimensional continuum of events .
-
Starting point of any form of physics are the explanations of the experiments involved.
-
-
-
-
-
-
-
-
-
-
Index
| Amorphous | page 47, page 108,
page 274, page 455
|
| Around matter | page 37, page 233,
page 270, page 276, page 279
|
| Axiom |
page 36, page 37,
page 213,
ref III
|
| Clock | page 74, page 75,
page 81, page 99, page 104,
page 106, page 145, page 195,
page 199, Ref III
|
| Continuum | page 23 , 24 , 26,
page 28, page 58,
page 71, page 96, page 206,
Ref 2
|
| Consciousness | page 71, page 206,
page 221
|
| Covariance | page 257, page 262,
page 269
|
| Curvature | page 93, page 97,
page 269, page 331
|
| Cylindrical Universe | page 301, page 439
|
| Definition (text) | page 47, page 48,
page 75, page 77, page 80,
page 82, page 253
|
| Density | page 58, page 258,
page 267, page 268, page 299
|
| Double bending | page 310, 311
|
| Duration | page 72, 75,
76, 79, 80,
81, page 101, 102,
page 119, page 132, page 170,
page 190, page 195,
199, page 210, page 213,
page 218, 222,
page 272, page 323,
page 443, page 470, Ref III
|
| Einstein's special principle of relativity | page 18,
page 104, page 114, page 144,
page 223
|
| Ether | page 116, page 123,
page 127, page 132, page 144,
page 146, page 168, page 208,
page 218
|
| Euclidean | page 38, page 83,
page 95
|
| Expanding universe | page 439
|
| Empirical | page 34, page 75,
page 108, page 114,
page 238, page 474
|
| feeling | page 212, page 221,
page 443
|
| Fields physics | page 407
|
| Flat | page 264, page 269
|
| Free will | page 454
|
| Freely (moving) | page 50, page 76,
page 234, page 239, page 265,
page 269, page 274, page 275,
page 293, page 475, ref 11
|
| Galilean frame | page 75, page 77,
page 80, page 82, page 107,
page 108, page 109, page 112,
page 119, page 145, page 146,
page 161, page 223, page 234,
page 269, page 272, Ref 6
|
| Galilean motion | page 17, page 104,
page 144, page 218
|
| gik | page 96, page 199,
page 235, page 258,
page 259, page 269,
page 276, page 281,
page 301
|
| Gik | page 269, 270,
page 281, page 292, page 295
page 301, page 301
|
| Govern | page 58, page 79,
page 92, page 204, page 382,
page 406
|
| Gravitational field | page 237,
page 270, page 274,
page 276, page 277,
page 280, page 288
|
| Gravitational mass | page 237, page 238,
page 240, page 277
|
| Inertial field | page 233, page 237,
page 247
|
| Inertial force | page 107, page 224,
page 233, page 237, page 240
|
| Inertial frame | page 107, page 108,
Ref 6
|
| Inertial mass | page 237, page 238,
page 277, page 307
|
| Interior of matter | page 239, page 240,
page 241,
page 268, page 270, page 276,
page 279, page 299
|
| Invariant | page 90, page 92,
page 96,
page 100, page 195, page 253,
254, 257, 258
page 264, page 268, 269,
page 447,
|
| Invariant velocity (of light) | page 127, page 146,
page 161,
page 168, page 171, page 193,
page 218, page 262, page 288,
page 451, page 474
|
| Lambda | page 300, page 301, page 303,
page 310
|
| Laplace | page 233, page 270,
page 275, page 434
|
| Law of inertia | page 76, page 108,
page 236, page 269, page 272
|
| Laws of nature | page 101, page 260, page 263, page 344, page 375
|
| Lemaitre | page 439
|
| Lobatchewski | page 35, page 212
|
| Lorentz-Einstein transformations | page 136,
page 145, page 194,
page 265
|
| Mach | page 108, page 310
|
| Manifold | page 23
|
| Mesh-system | page 84, page 87,
page 259, page 260
|
| Mercury | page 276, page 281,
page 310, 311, page 404
|
| Metrical field | page 56
|
| Michelson and Morley | page 82, page 132,
page 451
|
| Non-Euclidean | page 35, page 50,
page 60, page 83
|
| null-line | page 288
|
| Outside matter | page 267, page 268
See also "around matter"
|
| Philosopher | page 99, page 108,
page 343, page 443, page 449
|
| Philosophical | page 37, page 171,
page 241, page 299,
page 344, page 375,
page 404
|
| Philosophical issue | page 16, page 77,
page 134, page 151,
page 199, page 238, page 241,
242, 244, page 291,
page 299, 300, page 344,
page 383, page 404, page 474
|
| Philosophy | page 99, page 195,
page 241, page 449, Ref III
|
| Poisson's equation | page 270, page 299
|
| Poincaré | page 26
|
| Postulate of equivalence | page 224, page 236,
page 241, page 247, page 277
Ref III
|
| Potential | page 232 - page 234,
page 267 - page 270,
page 292, page 320
|
| Principle of causality | page 407
|
| Principle of correlation | page 134
|
| Principle of inertia | page 75
|
| Real space | page 56, page 455
|
| Reciprocity | page 223
|
| Relativity of simultaneity | page 72, page 171,
page 201
|
| Riemann | page 35, page 97,
page 212, page 296,
page 330
|
| Rotating | page 107, page 109,
page 233, page 280
|
| Simultaneity | page 72, page 101
|
| Special theory of Relativity | page 9, page 144,
page 264, page 269, page 288,
page 291
|
| Space and time |
page 58, page 100,
page 102, page 103, page 118,
page 119, page 150,
page 199, page 200, page 205,
page 263, page 264,
page 375, page 447, 448,
page 463, page 469,
page 473, page 475,
Ref I, Ref 7
|
| Space-Time | page 58, page 100,
page 194, page 197, page 209,
page 247, page 262, page 273
|
| Space-Time curvature | page 276, page 281, page 300, page 327
|
| Spatial distance | page 473
|
| Speed of light | page 245,
page 470, page 474,
Ref I, Ref 1
|
| Speed of gravitation | page 311, page 404, page 434,
Ref 8
|
| Translationary motion | page 17, page 112,
page 199
|
| Twin paradox | page 199, page 214,
page 218, page 223, page 439,
page 480
|
| universe (text) | page 105, page 166,
page 201, page 210, page 212,
page 243, page 300, page 301,
page 307, page 320, page 323,
page 324, page 375, page 439,
page 463
|
| Vacuum (was vacuo) | page 146, page 161,
page 236, page 238, page 262,
page 451, Ref 1
|
| Webster | page 170,
page 323, page 474
|
| World-line |
page 198, 199,
page 205, 206,
page 280,
page 469, 470,
474, 475,
480, Ref 10
|
Reflection I - General
The book "The evolution of Scientific Thought From Newton to Einstein" is a very powerful book, however there are still certain issues which I think are worthwhile to mention.
A central issue of the book is to unravel the laws of nature which are relevant for the total universe. The universe is a collection of large and small objects i.e. Black holes, stars, planets and asteroids. Within and specific on the surface all different types of physical process take place. Many of these processes are identical. It are specific identical processes and the small differences between these processes we humans like to study in order to influence or to predict how these process behave. As such we humans improve our knowledge. It is specific the evolution of this learning process which is the subject of this book.
The laws of nature are first of all descriptions of physical processes in our universe. These processes are not static but dynamic. That means all these processes are undergoing physical chance.
One of the major tools to unravel the laws of nature, by humans, is light to observe these processes. The point is that each measurement is also a physical process. However, and that is important, these physical processes, i.e. all what is involved to perform measurements by humans, is not part of what is happening in the evolution of the Universe and as such not part of the laws of nature, which is the subject of this book. That does not mean the problems involved with measurements can not be discussed, but they clearly should be seperated from the general theme of this book i.e. celstrial mechanics.
Two important concepts which are typical in this discussion are time dilation and length contraction. The deciding question are these two concepts physical. Maybe it is better to write are they physical physical compared to optical physical.
Time dilation is sofar as it involves the behaviour of clocks, which inner workings is specific based on lightsignals is a physical process. This behaviour in certain cases can be described by the Lorentz transformations.
Length contraction is not a physical process, length contraction is a typical optical physical issue.
When two identical rods are placed a fixed distance a part, each rod, observed from the other rod, seems to be smaller
as the other rod. This is typical an optical problem and is a function of distance.
When two rods are placed side by side and one rod is moving away there are two optical issues involved.
- The first optical illusion is indentical as when two rods are at different distances i.e. the length observed is smaller as a function of distance.
- The second optical illusion is a result because when the rods moves away the physical position of front end of the rod and the back of the rod are not observed simultaneous, because the front is further away. What the observer sees is the actual position of the front earlier. At the moment the front of the rod was closer towards the observer i.e. the rod looks closer.
- The second optical illusion is also observed when the train moves towards the observer. Again the observer will not see the front and the back simultaneous, but now it is the back that is further away. What the observer sees is the actual position of the back earlier. At the moment the back of the rod was closer towards the observer i.e. the rod looks closer.
What is the general lesson to be learned?
Photons and the speed of light are generally speaking physical not important for the physical processes that play part in the evolution of the universe i.e. the stars. That does not mean that electro magnetic processes don't play any part. All the processes in the unverse loose energy and matter because they emit electro magnetic radiation, but the importance is much less as what is called gravity or gravitation which causes the forces between stars.
What is now the overall conclusion?
That the laws which describe observations (i.e. light) and the true physical phenomena which involve physical changes should be clearly separated.
Reflection Ia - General Part 2
In this book two main concepts are space and time. The emphasis is on written text describing these phenomena. Part of this text can be in mathematical notation, but if that is the case a clear link between first what is physical or the physical phenoma versus what is mathematical counter part, should be implicated.
The universe, including We humans, exist in space and in time. From a physical point of view the two concepts space and time are closely intertwined. One cannot exist with out the other.
To solve this issue the concept space-time is introduced. Space-time is a mathematical concept. Within this view space and time are more or less are treated on equal footing as if they are the same i.e. mathematical the same, they are all dimensions. As such we can describe physical processes in 4D.
The is mathematical nothing wrong to use mathematical operations or concepts in 3D or 4D, also so to describe physical processes temporarily in 4D. The emphasis is on temporarily.
Consider a complete empty aquarium with a certain number of fishes. In order to understand the behaviour of one specific fish you can do two things:
- You can place a video camera outside the aquarium, at a fixed location, and monitor the behaviour during a certain period
- You can place a video camera attached to a second fish and monitor the behaviour (of the first fish) during a certain period
In the case of method 1 the next step is to measure the position of the fish in each frame of the video and store them in an array.
The same you can do with all the fishes and store the observations in different arrays.
In the case of method 2 you can also store the measurements of the fish in array, but now these measurements are not positions but distances between two fishes. That means what is measured is tells you something about two fishes and not one.
The next step is to attach a camera to the first fish but that has no advantage.
The following step is to attach a camera to a third fish such that each fish can monitor the other two, etc. The issue is that this methodology uses distances and not positions.
What we also want to know is the speed of each fish. This requires the introduction of clocks.
In my opinion method 1 is the easiest compared to method 2 in order to understand the behaviour of the objects in the aquarium.
The simplest reason is that when you use method 1 it is easy to calculate the results of method 2, but going backwards is much more difficult.
The main difference between the two methods is that in method 1 you use a fixed reference point and in method 2 not.
What is also important that in method 1 you use one video camera and in method 2 as many cameras as there are objects to study? Because we also want to study speed, each camera needs (at least) one clock. That means method 1 is the easiest.
The importance of method 1 is that you can use the same methodology to understand the behaviour of the planets around the sun.
The main problem is to define a point that is fixed i.e. a point with moves the least. This is the center of the Sun.
You can also use the same methodology to understand the behaviour of the stars in the solar system. The fixed point is now the center of our galaxy.
There is one additional advantage of this fixed point. This is the point called at rest. To be more specific to be called at absolute rest. However this is the worst point to claim that the speed of light is the same in all directions, because the point is at the center of a black hole.
The center of our galaxy and the center of the Andromeda galaxy are on collision course. That means a better fixed point is the center of gravitation of both. This is a better point to claim that the speed of light is the same in all directions.
Suppose there is a huge explosion at that point. Will that flash propagate at a sphere? Yes and no. As soon when that sphere reaches the outer regions of either galaxy it will be highly disturbed.
An almost similar problem is discussed at: Reflection 10 - The collision experiment.
Just some general thoughts.
Reflection II - The purpose of Science, definitions
The purpose of Science is to predict as accurate as possible the future based on the past.
To do that you need observations, both in the future and in the past.
These observations are descriptions of processes that are happening in your own vicinity but also in the whole of the universe.
These descriptions show the results of human observations, but most probably also the results of mechanical measurements and calculations based on these observations and measurements.
What you also need are experiments. These experiments are to improve our understanding at a more detail level and to challenge what is written and discovered by others.
The final step of Science is to find what the same is and what is different between all the observations. These are the laws of physics.
One of the most basic rules of science is to start from clear and unambiguous definitions.
Definitions specify the concepts used. As such they should descibe what concept is and what it does not mean. Both require examples. In that sense if you define the concepts absolute versus relative you need examples which describe absolute and which describe relative. If everything is relative the concept absolute does not make sense.
What is also important not to have two concepts which both mean the same or at least that there are no specific examples how to show the differences between the two.
A typical case is the postulate of equivalence which declares the two concepts gravitational mass and inertial mass the same, while there are no experiments which show any difference.
See also Reflection 4 - Absolute versus relative in Newton (Classical) versus Einstein. and
Reflection 4a - Absolute simultaneous versus relative simultaneous. (Relativity of simultaneity)
The use of definitions can also be called a postulate.
See next reflection.
Reflection III - The philosophy of Science, Experiments and Postulates.
Reflection II - The purpose of Science raises immediate a new issue: How should science be performed.
IMO the general rule should be: everything thing, related to physics, that is written should be as clear and unambiguous as possible.
We live in a constantly changing world. More important is that the world is constantly changing. What we want to understand is how this world is changing, but these changes have nothing to do with us. That means generally speaking all these changes are caused and evolve completely independent of any human activity.
To describe and understand these changes in time we use a clock. Again the changes (we are studying) have nothing to do with the internal operation of a clock except that clocks themselves can also be subject to these changes i.e. external influences. These influences can be such that clocks, which should indicate the same duration, don't.
As such it is important in order to describe and understand, to constantly adjust clocks such that all the clocks in use stay synchronised.
See also: Reflection 12 - 1D versus 3D Clock
See also: page 383
A very important issue when you want to do science is to perform experiments. One important rule to follow is that all experiments performed, should be described from a certain initial start configuration to a certain end configuration with all the intermediate steps performed, described in detail.
All these intermediate steps performed are very important.
For example: if you want to perform a certain round trip you can perform the following thought experiment: First a rocket goes from A to B with a constant speed, then a (different) rocket goes from B to C also with a constant speed and finally a (different) rocket goes from C to A also with a constant speed.
The problem with such a thought experiment that it is not realistic because in reality all types of accelerations
are involved which are not mentioned.
As such it is important that the initial configuration and the final configuration is the same i.e. all rockets involved
should be at rest.
Instead of configuration you could also use the words condition or (physical) state.
To make this simpler is when the start and end configurations are the same.
A typical case is the twin paradox involving two identical clocks.
- The starting conditions are two identical clocks both considered at rest in a certain frame. On clock is considered the moving clock inside a rocket which an engine.
- The first action is to start and stop the engine inorder to give the rocket a fast and constant speed in a forward direction towards a target.
- The second action is near the target to reverse the engine and to start and stop the engine inorder to decrease the speed of the rocket in the forward direction, with the intention to give the rocket a constant speed in the backward direction.
- The third action is near the starting point, again to reverse the engine and to start and stop the engine inorder to decrease the speed of the rocket to zero.
What this experiment shows that the initial and final state are the same and that both clocks are at rest.
A different rule to follow is that always a closed system is assumed, except if otherwise indicated.
A typical case in point is the 'experiment' described at page 243. In that case some unseen hand is involved. This is typical not a closed system.
What is physical possible, is the behaviour a star which is ejected from a cluster of stars. Such a star can be considered a fast moving object (with a constant speed) in interstellar space. If that is what you mean, than mention this.
A completely different issue is to what are postulates versus axioms.
My definition of postulates are the simplest basic concepts in physics. Axioms are the simplest concepts in mathematics. The reason why I make this distinction is because the physical 'world' and the mathematical 'world' are two complete different 'worlds'. In fact the word 'world' can not be used in both cases.
In certain cases the physical 'world' and the mathematical 'world' are overlapping, but generally speaking they are not. This means that physical concepts can incorporate mathematical concepts.
One of the basic postulates is that all the physical concepts should be explained by means of experiments.
An other postulate is that there are observed quantities and calculated quantities.
Observed quantities are based on direct observations or measurements. Calculated quantities are calculated based on
observed quantities and calculated quantities.
As such a position is an observed quantity and a velocity or acceleration an calculated quantity.
A very important issue postulate is: The explanation of anything physical of any physical process is in the physical details of the process itself.
If there is a dead body and the docter declares that this is a murder case, than it is important to find as much physical evidence about allmost everything, in order to understand what happened in the past and to pinpoint the precise cause.
For all physical processes the same is the case: Understanding lies in the details.
There are generally speaking two types of processes: stable and unstable processes.
Stable processes, as the name suggest, exist in the same configurtion over a very long time. Unstable processes can happen in a split second but also the configuration changes rather quickly.
A typical unstable process are the high and low pressure configurations on the surface of the earth. A typical stable process are the movement of the planets around the sun.
Stable processes can be described with mathematical precision. With that we mean the physical relations between the individual parts that constitute the total. The physical relations are expressed in mathematical equations, the mathematical parameters involved are directly related with physical parameters which can be measured.
These equations are descriptions, also called laws of nature. One thing is important: The laws of physics (the subject of)
have nothing in common with pure mathematics.
One typical stable physical process is a clock. The behaviour of a clock can be described by means of mathematics, but this mathematics should reflect the internal operation of (or lack of) the clock. For example: an hourly glass operates satisfactory when placed on the surface of the earth, but not when moved i.e. placed in a moving ship at sea. The same time of limitations exist for all clocks, specific when the innnerworkings is based on lightsignals.
A related issue is the physical behaviour of lightsignals in general i.e. photons and all electromagnetic phenomena.
If you want to know the speed of a lightsignal than, in order to do that, you need a clock. If the internal working of the clock operates on lightsignals than of course you have problem.
Along the same line:
The explanation of any physical process can never be, solely, by means of mathematics. (Physical laws are descriptions)
See also: Reflection 7 - Physical space versus Mathematical space.
See also: page 241: Postulate of equivalence.
See also: page 277: Equivalence between energy and mass
Reflection 1 - Observers, humans and light.
Throughout the book the importance of observers is mentioned. That is acceptable. In fact, it is we humans, who want to understand how nature operates, what the laws of nature are. It is we humans, who act as observers, who perform the experiments and perform the measurements to unravel these laws.
The problem is that we should be careful when we do that. It is easily to make mistakes because there is a chance that we are biased and that we make conclusions from our perspective. The issue is that the laws of nature have nothing to do (in general) with what we humans on earth think or do. They operate completely independent from us. That means, when we use our senses we have to be careful to make conclusion from our own perspective.
The most important tool we use is our eyes. We use light. But it is important to note that light itself is also a physical element i.e. photons, with it own limitations. In fact when we use light we get a slightly distorted image because photons (electro magnetic radiation) are also modified when they travel from a source to the destination i.e. our eyes.
One important measurement tool is a clock. Many clocks in order to operate use light signals. There is nothing wrong with this except when you move such a clock its behaviour will change when you move such a clock in the direction of the (direction of the) light signal. In that way the path will be longer and the clock will tick slower.
A closely related issue is the speed of light and the postulate that this speed is invariant or is constant. The real issue is to what extend we can claim that the speed of photon's is everywhere the same? Or is that not what we claim?
Why mention that this is only true in vacuum?
Reflection 2 - Sensory continuum.
In the first chapter the use of the word continuum is mentioned often. As in the meaning of the sentence: the universe evolves continuous, time flows continuous.
That is true. How ever in real life, when you are involved with science, every thing that we do is described at a certain moment i.e. discontinuous.
Events are also discontinuous. That means the three events E1, E2 and E3 are generally speaking different in both space (position) and time. Independent of what we humans might think (observe), otherwise this are not three events.
Reflection 3 - Length contraction.
The text at page 208 indicates that length contraction has something to do with the movement of the rods involved.
Of course when something moves away from us that what we observe becomes smaller. This can be a rod or a clock.
Suppose there are two rods involved: one rod A which stays at home and one rod B which moves.
The question what happens when the moving rod B stops (relative to rod A). The most logical answer is: that at that moment the length of rod B stays the same.
The next question to answer is: Is there a difference in length between rod A and rod B.
Next suppose rod B moves back to us. What we observe is that rod B becomes larger. This can be a rod or a clock.
When rod B returns and we compare the length between rod a and rod B they are the same. This gives the impression that nothing physical has happened.
In case when we used clocks and we compared the ticks there is a difference. This means something physical happened with the clocks.
Reflection 4 - absolute versus relative in Newton (Classical) versus Einstein.
When you want to discuss the meaning of words the meaning of each word should be clear and unambiguous, specific if you want to discuss two competing words like absolute and relative.
Specific if you want to make something clear you should give examples when each applies. As such it does not make sense to call 'all' physical phenomena relative and that there are no absolute physical phenomena.
See the end of page 16 and page 103
and also page 449.
To get an idea about Newton's opinion read:
Reflection 2 - absolute versus relative in Newton's opinion which is part of the Book Review: 'Newton's Principia'.
My understanding is that Classical Science does not use the words absolute and relative. Classical science is based around the following concepts: positions in space, distances, speeds and accelerations. One clock is used and one frame.
In classical science the difference between observed and calculated values or parameters is much more important.
Positions and clock readings are observed values. Speed is a calculated parameter. Acceleration is also calculated.
To call acceleration an absolute does not make to much sense, because specific when an object moves in a circle the direction of acceleration constantly changes.
What is very important in the book are the position and the velocity of the observer.
See page 100 and page 101.
It is easy to agree upon that when the position of an observer changes what he or she observes changes. But that does not mean that what is observed also changes. The reverse can also be true. That means when the position of the observer does not change his or her surroundings can change. In fact that is what we want in order to unravel the laws of nature. We want to study the evolution of the Universe, all the changes that take place independent from the point of view of a single observer.
A case in point is a merry go round. From the point of view of an observer in the merry go round, the merry go round is at rest and the ground is turning. From the point of view of observer not in the merry go round, the merry go round is turning and the ground is at rest. The simplest conclusion is to start from the observations from an observer on the ground.
A similar conclusion you can reach from an observer at the center of the earth, or better at the center of the Sun, or better at the center of our Galaxy.
Reflection 4a - absolute simultaneous versus relative simultaneous. (Relativity of simultaneity)
When you want to discuss the meaning of words generally speaking the meaning of each word should be clear and unambiguous.
In this reflection the differences between the concepts absolute and relative are discussed and specific between absolute simultaneous versus relative simultaneous.
The word simultaneous means that two events happen at the same moment at different positions. At page 170 the concept coincidence of events is discussed. That means simultaneous at the same position. In this reflection we mean at different locations.
If you want to discuss something you must agree which each other on certain definitions. The first things to agree upon is, that there exist an universe and that at every instant throughout the universe events take place. Any event represents a change. This can be a change in position of a elementary particle, the emission of a photon, an explosion (which involves million of changes) or what ever you want. The point is that we call all the events that happen at the same instant simultaneous and two events that happen at different instants non simultaneous. You can also define: Each event, of all the simultaneous events that happened at the same instant, happened non simultaneous with an event that happened at a different instant.
This is all physics and humans have nothing to do with this. The problem is that humans are involved to decide if two events happened at the same instant i.e. are simultaneous and that is not so easy. Part of the problem is that in order to decide we need observations and these observations need light signals which involve a delay between when an event happened and when we see or observe this event (this is also an event). This delay is longer the further away the event was. This delay is the time between (the instant of) the physical event and the observation event.
This problem becomes more difficult when two simultaneous events are involved, specific when the distance between each event and us is different. This implies that the two delays involved (which each between a physical event and an observation event) are different. When that is the case we will observe the two simultaneous events as non simultaneous events.
However the reverse can also happen: It is possible that we can observe two simultaneous events as simultaneous.
It is important that all what we are discussing here is physics are physical processes which happen all the time throughout the whole universe.
IMO all of this has nothing to do with concepts like absolute and relative, but if you want to use them, specific to make a distinction within the same concept (like event, position, velocity, acceleration) each use should be clear.
For example the use of absolute is unambiguous if you use that word for all physical observations and the use relative becomes unambiguous if it is used as part of a calculation based on physical observations.
However it is slightly more complicated. Physical observations as explained above are human depended. That is not what you want. As such with absolute we mean all physical observations reflecting the physical situation at the same instant.
The same issue is involved when want to use Newton's Law. The first step is to perform a set of observations at specific instants.
This is repeated for the same set of observations at different instants.
The second is process all these observations and to calculate a set of observation at the same instant. These observations are simultaneous and you could call them absolute. This is also done for the same set of calculations at different instants.
The third step is to calculate velocities and accelerations of the set of objects studied and finally the masses of all these objects.
|
An important issue, not yet discussed, is the concept time. As mentioned above, simultaneous events are physical changes which all happen in the entire universe at the same instant. In fact that is what you want: throughout the entire universe you want clocks which all tick (add 1 count) at that same instant. Not at a certain instant but allways. That mean all the clocks should run synchrone and simultaneous.
To implement such a system what you need is a 3D grid, with at each point a clock. In such a grid each clock is surrounded by 6 clocks (2 in the x direction, 2 in the y direction and two in the z direction).
Now take one specific clock.
When this clock counts 10 and all the clocks are correctly synchronized than at that same instant all the clocks in the universe should count 10.
However that is not what is observed
Assume that the size of each clock is half the distance between each adjacent clock. In that case, when your clock counts 10 all the 6 adjacent clock show 9 counts. That means it looks if they run 1 count behind, but that is what is observed. In reality they don't as long as this difference stays exactly the same.
The distance between your clock and the clock in the x direction we call dx. This clock runs 1 count behind (as observed). There is also a clock at a distance 2dx. This clock runs 2 counts behind. etc. In the y and z direction the situation is the same.
Using these clocks, thoughout the entire universe, you can decide for any set of events if they happened simultaneous or not, by reading the nearest clock.
One issue is not mentioned and that all the clocks should be at rest in all directions. But when all the clocks in use are synchronised as described, this is no issue.
Reflection 5 - Simultaneous versus Not-simultaneous events
If two events are simultaneous or not is a physical issue and has nothing to do with humans or human observations. That does not mean that humans are not involved.
Two events are not-simultaneous if one event is original caused by an earlier event. As such we can speak of a cause and an effect. In between the original event and the final event a sequence of events can take place which are all not simultaneous.
In this specific case we are considering two sequences of events i.e. sequence of events "A" and sequence of events "B".
The first event of sequence "A" is event "A1" and the final event is event "A9".
The first event of sequence "B" is event "B1" and the final event is event "B9".
The connection between event A1 and event B1 is, that they both happen at the same time and place "X". That means they can be considered simultaneous. The final events "A9" and "B9" also happen at the same time and place "Y". They are also simultaneous.
In between event "A1" and event "A9" there are 7 events i.e. "A2", "A3" etc.
In between event "B1" and event "B9" there are 7 events i.e. "B2", "B3" etc.
The major difference between the two sequences is that the physical path followed between "X" and "Y" is different.
Generally speaking the events "A2" and "B2" are not simultaneous.
The whole purpose of this experiment is the question: is it possible that with every event "An" there is also a simultaneous event "Bn"?
IMO the answer is: yes.
The whole issue is when event "A2" happens there also should happen something simultaneous in sequence "B". This is event "B2" etc.
This same problem is also discussed at page 170 where it is called: coincidence of events
B
B B
B B
B B
B B
B B
XAAAAAAAAAAAY
|
|
In the picture on the left there are two sequences of event.
- Sequence "A" follows a straight line from X to Y
- Sequence "B" follows a more bended line from X to Y
|
The general question to answer is: how do you establish the corresponding pairs of events in both sequence 1 and sequence 2 which are simultaneous. This example is rather symmetrical. What we want is a more general answer.
To find the answer is, the total length of each of the sequences is important.
Reflection 6 - Frames.
Throughout the book the concept of frames is used. Why? Why not using one type i.e. one reference frame?
The concept of frames introduces all kinds of problems, specific when different frames are used: Inertial, Galilean, Euclidean, Non-Euclidean and rotational. Even when you consider only one type, there are complications. Because what is the best frame to select.
Generally speaking a frame describes an image of the total universe with infinite size. A frame is centred around an observer which is considered at rest in that frame (in his universe). The speed of light is the same in all directions and invariant i.e. constant.
All the frames are identical. In a Galilean or inertial frame the difference between each frame is a constant speed v.
The real issue is not so much how much is the speed of light, but how is the speed of light and the speed v actual measured.
Assume for simplicity that the speed of light is 300000 km/sec.
Consider the following two examples:
- When the difference between two points A and B is 300km and each point has a clock and both clocks are 'synchronised' than a light flash emitted by point A will be received 1 msec later by point B.
- When a rocket travels from A to B and the travel time is 10 msec then the average speed is 30000 km/sec or 0.1*c. The distance between A and B is also 300 km
The first example is a test if both clocks are properly synchronised.
The synchronisation test involves that when the light flash is emitted at point A at 10h 0m 0s it should exactly be received 1 msec later at point B. Exactly the same should be measured in the reverse direction.
The second example first requires the synchronisation test and also should be performed in both directions.
The first example (the synchronisation test) should also be performed with different speeds of point A and B
The second example does not use a moving clock inside the rocket.
Both clocks used are attached to the frame.
Reflection 6a - Physical at rest versus mathematical at rest
Let us start with the concept mathematical at rest because that is the easiests.
Within the mathematical world there is no concept at rest because at rest
Reflection 7 - Physics versus Mathematics versus mathematical physics.
Physics involves the study of the behaviour of the evolution of the Universe in 3 dimensions. By studying physics, we improve our understanding of the physical process hapening in nature. Understanding implies to find similarities and differences between these processes.
One of the most central features are objects. One of the central themes are the internal composition and structures of objects i.e. the materials from which they are made. This field of study is called chemistry including quantum mechanics.
A different theme is the study of objects large, small and very small through space. This field is called celestrial mechanics. This is the topic of this book.
Mathematics is a whole different field of study. In some sense mathematics involves an abstract world. A world with abstract objects, equations and numbers.
Many processes in physics are stable or can be studied by precise defined experiments. Starting point of the investigating of stable processes or experiments are measurements. There are many different types of physical measurements. They can be human related, related to chemical processes, about stellar objects or related to the composition of the universe. These measurements result in numbers. Performing measurements over a certain time and combining the numerical result in laws expressed in simple mathematical relations or differential equations.
This field is called mathematical physics.
Reflection 7a - Physical space versus Mathematical space.
Physical space is the Universe. Physical space includes all that exists.
Physical space exists in time. Physical space is not empty. Physical space is three dimensional.
Mathematical space is in some sense a strange concept, because mathematical space does not exist.
Mathematical space is much more a mathematical description of physical space. Mathematical space is empty.
Mathematical space can consist of an X axis, a Y axis and a Z axis, perpendicular on each other. The center is called the origin and its size is considered finite. In that case mathematical space is three dimensional.
Mathematical space can also consist in of a W axis, a X axis, a Y axis and a Z axis. In that case mathematical space is called four dimensional. A visible conception of such a space is difficult.
Mathematical space in principle can consist of any number of axes.
Physical space is similar as Mathematical space. The major difference that Physical space exists in time.
Time is called the 4th dimension.
Physical Space is infinite (in both positive and negative dimension) as opposed to finite. However the physical implications are unknown. The problem is that Physical Space cannot be called finite, because that imposes a boundary, which physical can not be vindicated?
Physical Space, its time dimension, its existence is also infinite, in the past and in the future. The time dimension cannot be called finite, because that imposes a boundary, which physical can not be vindicated.
General Relativity allows that Physical Space is bended. Observations reveal that the path of a light ray from a star near a second star is not straight but bended. There is nothing wrong with this, because the bending is observed as a function of the visible distance between the two stars.
In the same situation, to call physical space bended, requires a clear explanation of what bended means.
A much more important issue that there exist only one Physical space i.e. one universe.
To unravel the laws of nature, which are valid for the total universe, you only need one reference frame.
Reflection 7b - Physical dimensionality versus Mathematical dimensionality.
Mathematical dimensionality is based on the concept of geometrical shapes. That means you can fill mathematical space with objects, but these objects have no mass.
The geometrical shapes are: points, lines, flat planes, and 3D shapes like cubes, spheres and pyramids.
A mathematical point has dimension 0. A mathematical line has dimensionality 1 and a flat plane 2.
The surface of a sphere and each 3D shape has dimensionality 3.
The subject of Physical dimensionality are objects or bodies and is also based on the concept of geometrical shapes, however all the objects have mass.
The main difference with mathematical shapes is that all physical objects are 3D. A physical point is always 3D, otherwise it does not exist (in time).
Physical objects have surface. A cube consists of 6 flat surfaces. The surface of a round about has the shape of a sphere.
See also page 33
Reflection 7c - Space and time versus Space-time.
In the physical world space and time are closely linked and cannot be studied separately. In fact at any instant the total universe is in a certain state and this state changes continuously. You can also describe the universe discrete or in finite time steps. That means at t0 the universe is in state 0, at t1 in state 1 at t2 in state 3, etc, etc.
Newton's Laws uses a similar concept. Each simulation of the solar system starts with the initial conditions of the positions and velocities of all the planets at t0. The positions are observed and the velocities are calculated based on 'previous' observations.
Based on a step size dt and the mass of each planet, first the accelerations, next the velocities and finally the positions for each and all the planets are calculated at t1. This same process can be repeated for t2, t3, t4 etc etc.
All the planets move more or less in the same plane. This makes it easy to draw the paths of all the planets on a flat computer screen in 2D. The results are more or less circles with different diameters centred on the Sun.
The 'problem' with that approach is that sooner a later each circle becomes completely filled and then it becomes 'impossible' to see where the specific planet is.
A different way of show the result is in the form of a Space-time diagram. However to show each position (x,y,z,t) of all the planets on a flat computer screen becomes messy. Even when you remove the z parameter this still is rather messy.
Reflection 8 - Newton's Law - The movement of the planets
In order to simulate the movement of the planets and or to predict the future Newton's Law can be used.
- The first step in applying Newton's Law is to perform observations. In the case of the movement of the planets to observe the positions of the planets at as much different moments as possible. These are the so called observed parameters (observed time, angles).
- The second step is to define a 3D reference frame. For simplicity a frame with as origin the center of the Sun.
- The third step is to calculate the x,y,z positions of the planets at regular intervals (calculated time) based on the observations. These are the calculated positions. (Forward transformations). The values at t=0 are called the initial conditions.
- The fourth step is to calculate the masses of all the planets and the Sun using Newton's Law.
- The fifth step is to calculate the positions of the planets at some future moment tn.
- The sixth step is to perform a so called backward transformation. That means to calculate the observed parameters from the calculated positions at tn. These predicted values can then be checked against the actual observations at tn.
The fourth step is the most difficult. The easiest way is to start with 2 objects (Sun Earth), then three (Sun Earth Jupiter) etc. etc.
The basic idea behind Newton's Law are two steps for each object at each moment tn
- First the sum of all the forces on the object considered caused by all the other objects is calculated.
- Secondly the gravitational (driving) force of the same object is calculated based on the assumption that the sum of the gravitational force and the total force is zero.
Using the calculated gravitational force the acceleration, speed and the new position at tn+1 can be calculated (using the mass of the object)
What is important that IMO the concepts like absolute and relative are not used.
In some sense you can call the world described in step 4 an absolute world. In fact that is the physical world in which the real physical processes take place. This is not the world we observe, because what we observe is a world in the past.
In step 3 and step 5 transformation calculations are used. In step 3 the transformations require the speed of light. This is because the observations at tn define the position in the past. To calculate the actual time of these positions the speed of light is used i.e. tn - distance/c. Next the actual positions can be calculated in a rather straight forward way.
In step 5 the reverse is done i.e. going from the present towards the past.
It is important to mention that each observer (observation point) requires different transformation equations.
As mentioned step 4 defines the physical world. You can call it absolute, but that does not make sense. More important is that it is observer independent.
See also page 101 and page 105.
The biggest problem with Newton's Law is that the present forces don't act instantaneous (in the physical world) but towards positions in the past. To calculate these positions require the speed of gravity. You can define the speed of gravity equal to the speed of light, but physical the speed of gravity is completely different. The gravitational field is not bended around objects.
Reflection 9 - The shaking problem - Black White.
ab
AB
Fig 1
|
Consider a square of size 2 by 2, subdivided of 4 squares of 1 by 1.
In the top line the squares are white. These two lines are marked a and b
In the bottom line the squares are black. These two lines are marked A and B
|
This configuration (See Fig 1) is called stable.
There are two combinations which we can place the two white squares i.e. ab and ba
There are two combinations which we can place the two black squares i.e. AB and BA
Which each of the 2 white combinations there 2 black combinations. In total 4 i.e. abAB, abBA, baAB and baBA.
There exist also a second stable configuration in which all white squares are replaced by black squares. In total also 4
combinations i.e. ABab, ABba, BAab and BAba. This brings the total of all the stable combinations to 4+4=8
The total of all combinations is 24:
abAB, abBA, aAbB, aABb, aBbA, aBAb,
baAB, baBA, bAaB, bABa, bBaA, bBAa,
AabB, AaBb, AbaB, AbBa, ABab, ABba,
BabA, BaAb, BbaA, BbAa, BAab and BAba
There are 4 groups of each 6 combinations. In each group of 6 combinations you get 3 groups of 2 combinations. As you get 4*3*2 is a total of 24 combinations.
The final result is there are 8 stable combinations and 24-8= 16 mixed combinations.
abc
ABC
Fig 2
|
Now let us study rectangle of 3 by 2 i.e. 3 white squares abc and 3 black squares ABC. See Fig 2
There are 2*3 = 6 combinations which we can place the two white squares i.e. abc, acb, bac, bca, cab and cba
There are 2*3 = 6 combinations which we can place the two black squares i.e. ABC, ACB, BAC, BCA, CAB and CBA
|
Which each of the 6 white combinations there are also 6 black combinations. In total 6*6 = 36.
There exist also a second stable configuration in which all white squares are replaced by black squares. In total also 36
combinations i.e. aBab, aBba, Baab and Baba.
In total there are 720 combitions i.e. 6*5*4*3*2
The final result is there are 72 stable combinations and 720 - 72 = 648 mixed combinations.
When you divide both by 72 you get: 10 total combinations or 1 stable combination and 9 mixed combinations.
abcd
ABCD
Fig 3
|
Now let us study rectangle of 4 by 2 i.e. 4 white squares abcd and 4 black squares ABCD. See Fig 3
There are 2*3*4 = 24 combinations which we can place the two white squares
There are 2*3*4 = 24 combinations which we can place the two black squares
|
Which each of the 24 white combinations there 24 black combinations. In total (2*3*4)*(2*3*4)
There exist also a second stable configuration in which all white squares are replace by black squares. In total also
(2*3*4)*(2*3*4)
The total number of all combinations = 8*7*6*5*4*3*2. There are 2*(2*3*4)*(2*3*4) of stable combinations
When you divide both by 4*3*2 then you get 8*7*6*5 total combinations and 2*2*3*4 stable combinations.
When you divide both by 8*6 you get 7*5 total combinations or 1 stable combination and 34 mixed combinations.
What this shows that the more squares the longer it takes but the initial position will appear again and again and again.
What this also shows that this nothing has to do with probability, nor with the concept of time but that this is physics.
We assume that all the squares are equal and if you perform this experiments with equal sized balls (a predefined number of times) you can predict what the outcome is (most probably mixed), at the same time the outcome can also be wrong (i.e. stable).
On the other hand if you perform this experiment with not equal sized balls the larger balls will "float" on top of the smaller balls because gravity becomes an issue.
This can only be established by performing real experiments.
Reflection 10 - The collision experiment.
Consider a certain object A (with observer A) which moves in a straight line with a constant speed through (empty) space.
At regular intervals object A emits a flash of light.
Consider a second object B (with observer B) which moves in a straight line with a constant speed through (empty) space.
At regular intervals object B emits a flash of light.
At a certain moment there is a collision between the two objects at point P which also emits a flash of light. This collision is called a coincidence of events.
After the collision both objects continue to move in a straight line with a constant speed, however both in a different direction. Both objects (A and B) continue to emit light flashes
See also page 170 where a collision i.e. a coincidence of events between two automobiles is discussed. Such a coincidence is an absolute.
Consider a third object C (with observer C) which moves in a straight line with a constant speed.
At regular intervals object C emits a flash of light.
Consider a fourth object D (with observer D) which moves in a straight line with a constant speed.
At regular intervals object D emits a flash of light.
At a certain moment there is a collision between the object C and D at point Q which emits a flash of light.
We can also introduce two more objects E and F, who collide at point R.
There can also be a collision between object A and object F at point S.
It is very important to compare this experiment with page 171 where the passing of two uniformly moving trains is discussed.
In summary.
What we have is a collection of objects (and observers) which move in straight lines and which emit light flashes at what are called emission-points
What we also have are collisions between these objects at what are called collision-points. Each of these collision-points emits flash of light in the form of an expanding sphere.
From a physical point all these collision-points are considered an absolute and each of these collision-points
is at a centre of an expanding sphere.
For the moving objects the story is different.
Considering object A and Observer A, both are at rest in their own reference frame. Object A emits a flash of light at regular intervals and observer A is in the centre of the expanding spheres. For object B and Observer B the situation is similar.
When we consider object A in more detail: object A can also be involved with collisions. First there is a collision with object B (point P) and a little later with object F (point S). Those two events (collisions) can not be simultaneous. This is also indicated because the radius of the two spheres (at point P and point S) are different.
Next we can draw a line (world-line) between point P and point S and all the spheres on that line, which indicate the flashes emitted by object A. All the radei are different (at a certain instant), which indicates that the emission-points are not simultaneous.
To get a better physical picture what is involved, consider collision-points only in the horizontal x,y plane. The z axis is the time axis. In that case point P is at x1,y1,t1 with t1=0 and point S is at position x2,y2,t2 with t2>0
Picture 1
|
Picture 1 at the left shows the world-line of observer A in Space-Time in two dimensions i.e. the X,Y plane.
The world-line starts at the bottom. The world-line is divided in two parts subdivided by point "P" in blue. This is the (first) collision-point of object A with an other object. The first part shows two emission-points in green with the letter "A".
The second part shows shows three emission-points with the letter "A" in red.
It is important to remark that picture 1 shows 6 circles in the X,Y plane. In real this should be 6 spheres in the X,Y,Z space.
At the left part shows the 3 dimensions, centred on the origin O in gray. The t axis defines the time dimension.
The two X,Y lines in black define the plane at present.
When Picture 1 is selected two more events are shown: one emission-point with the letter "A" in red and a second collision-point with the letter "S" in blue. That means the world-line through the red events is marked by two collision-events "P" and "S", however each of these points can also be an emission-point.
This raises a difficult issue, because point "A", in this example, is involved with three reference frames in which point "A" can be considered at rest. The question is now: to which of these frames belong the two points "P" and "S"
|
Picture 2
|
Picture 2 at the left, shows 6 collision points.
The first collision point is point "P". The other collision points are identified with the letters "Q","R","S","T" and "U".
Each collision is called a "coincidence of events". See also page 170. My understanding is much more that the collision it self is only one event. It is a collision-event or collision-point.
What is much more important that general speaking most of the collisions are not simultaneous, except maybe some?
Figure 2 contains 6 event-points in a rather small reference frame. But this is not completely true. The reference frame can be large and it can contain thousands of collision points, but, and that is important, they are completely object and observer independent. Of course underlying each event there is a cause, but the flash generated is independent of the speed of the object or the mass of the object. And, that is also important, this is for all collision points the same.
That is why you can treat all these events in one reference frame. In some sense each collision event is more or less random and that is not the case considering the emission-events of an observer in empty space which follows a straight line.
|
Picture 1 and Picture 2 show what is called Space-Time, not in 3 X,Y,Z dimensions but in 2 dimensions.
Reflection 11 - Gravitational mass and forces versus Inertial mass and forces
To understand Gravitational mass and forces is the simplest because it involves all objects or bodies in the entire Universe. This field of study is called celestial mechanics.
The gravitational forces are the postulated forces acting between all bodies in the universe.
Each object produces what is called a gravitational field. The strength of this field can be calculated by using a unitary mass particle. I.e. a particle with mass= 1.
In order to calculate the Gravitational mass we use Newton Law or GR and observations. The observations are the position of each object considered, at a regular interval i.e. t0,t1,t2,t3, t4 etc. Using these observations the first step is to calculate the gravitational mass of the planet Jupiter as a function of the mass of the Sun. The next step is to add one more planet like Mars, and to the calculate the mass of each: Jupiter and Mars. This is repeated until the gravitational mass of all planets are calculated including the Earth.
Suppose we want to know the gravitational mass of a billiard ball. To do that you drop the ball from a certain height and you measure the performance i.e. the position at regular intervals. Using Newton's law, in the exact same way as you calculate the gravitational masses of the objects in the solar system you can calculate the gravitational masses of the billiard ball.
See also page 238
To perform this experiment in real, to perform all the necessary observations is very complicated, because the two masses are very differently in size, but such an experiment can be performed and that is what counts.
The final question is what is inertial mass and inertial forces?
Besides gravitational forces which are in some sense permanent, we can define other forces which often are of a more temporary nation. Any ballistic experiment consists of two specific events. At the first event matter is converted in to energy to give the ballistic device its initial condition. At the end more or less the reverse happens. During the flight the ballistic device can be considered a free moving object and can be described by Newton's Law or GR. No special masses are involved except gravitational masses.
Reflection 12 - 1D versus 3D Clock.
The 1D Clock is an optical clock which operates which a light signal in 1 direction. At the center of the clock is a light source which emits one light pulses in one direction. A 1D clock operates along one axis and consists of two mirrors. This initial pulse at first, moves towards the right (assumed), is reflected against the mirror at the right, moves towards the left, is reflected, moves towards the right and passes the center of the clock. This defines one tick. There after the whole processes repeats itself, at infinite.
It should be mentioned that the mirrors are very small, just large enough to reflect the pulse. The light pulse is nowhere amplified.
The 3D clock in principle works the same as a 1D except that the 3D clock contains 3 times the same functionality (hardware) of the 1D clock. That means a 3D clock contains 3 light sources which each emits a light pulse in one direction. A 3D clock operates along 3 axes which direction each is perpendicular upon the others. The same as the 1D clock: the light pulses are not amplified.
A 1D clock consists of one oscillator which ticks. A 3D clock consists of 3 oscillators. In order to function properly all these 3 oscillators should run synchronous i.e. all tick at the same rate.
The question is does each 3D clock operates in any frame. With a frame I mean a clock moving in a certain direction with a certain speed. With different frames I mean different clocks, each moving with different speeds, each in a different direction.
First consider a universe with only one clock. By definition you can call this clock at rest and by definition this clock works properly. In stead of by definition you can also write: as a postulate.
Next consider a universe with two clocks. In principle both clocks can be at rest and then they work properly. They can also move and rotate around each other, like a binary system. If that is the case the 3 internal axis of the clock will also rotate and the clock will stop functioning properly.
To get a better idea what is involved select: The operation of a Clock in a Centrifuge. In the clock discussed the reflection mirrors are large. Each clock has 6 mirrors in side a box. The size of each mirror is the same whole size of the wall of the box. In this 'reflection' the size of the mirrors are small. The result is that almost immediate when the linear accelerator or centrifuge starts to move the clock will stop functioning properly.
Finally consider a Universe with many clocks all moving in different directions and with different speeds. My guess is that none of the clocks will work properly.
What that means that if you want to do physics you should consider a universe containing an imaginary grid with at each grid point an imaginary clock, all at rest.
Feedback
If you want to give a comment you can use the following form Comment form
Created: 6 February 2019
Updated: 12 March 2019
Updated: 5 May 2019
Updated: 22 June 2019
Updated: 21 July 2019
Updated: 10 January 2020
Go Back to Book and article Review
Back to my home page Index


