Hypervelocity Runaway stars (HVSs) and Black Holes

Answer Question 1 - definition

Hypervelocity stars are stars outside our Galaxy with a speed exceeding the escape speed of our Galaxy.
In order to simulate Hypervelocity Runaway stars you need at least three objects. The theory behind those simultions is the slingshot effect. For more detail see: Sling Shot Effect and Gravity Assist

In order to demonstrate Hypervelocity stars a Visual Basic program is avaible.
To get a copy with the source and to execute the program select: VB HVstar.zip
For a description of the program select: VB HVstar x.htm
For implemtation details select: implemnt.htm

Answer Question 2 - Two binary stars and a third star

One possible solution to simulate a "HV star" is by means of two binary stars and a small single star. The theory behind this simulation is that the small star moves towards the binary stars. During the approach four things can happen:

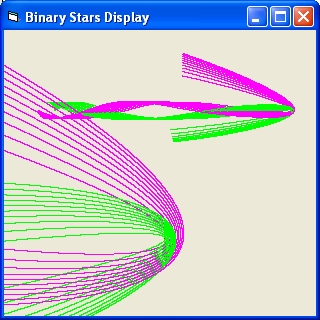
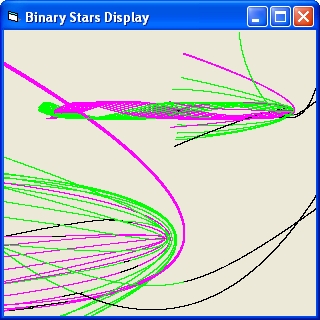
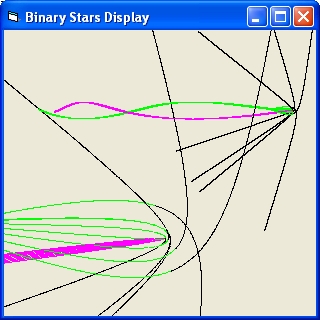
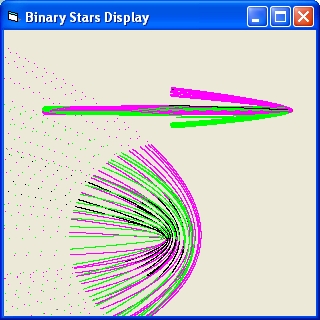
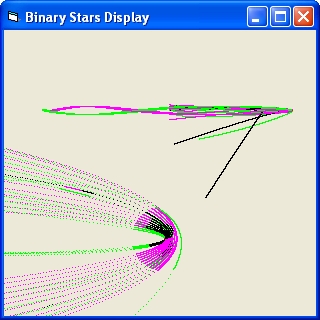
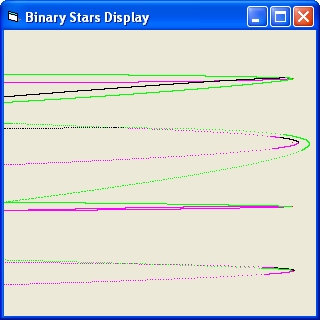
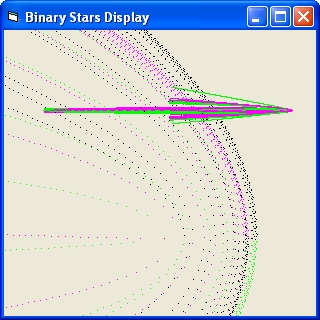
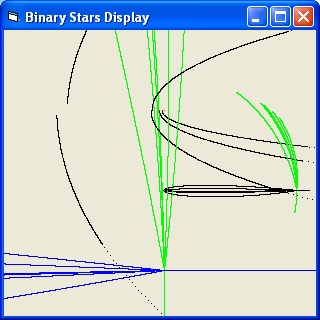
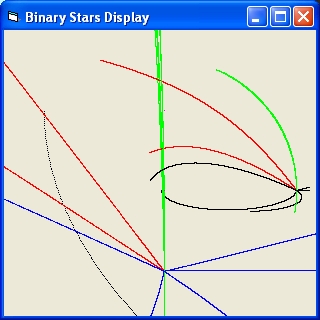
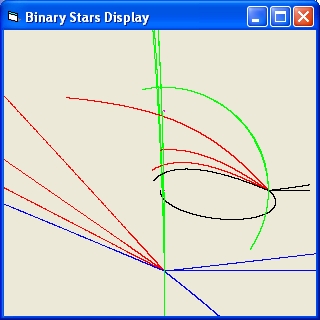
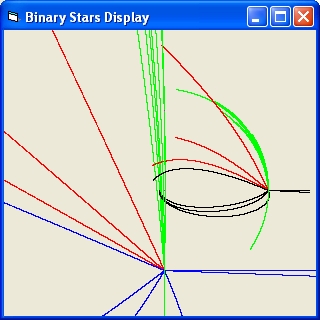
1. The small star will immediate collide with one of the binary stars
2. The small star will make a dance around the binary stars and then collide.
3. The small star will make a dance around the binary stars and then be ejected
4. The small star will immediate be ejected

When the third star is ejected the speed is small. That means you need more of these encounters to speak of a High Velocity Star.
The initial speeds of the single star m3 is below the escape velocity of the binary pair (M = m1+m2 v = sqr(2*G*M/R)).
In order to evaluate each simulation two parameters vlimit and rlimit are used

• vlimit is defined by using the escape speed v^2 = 2 * G * M/R
  with r = v * dt we get: v^2 = 2 * G * M/(v * dt)
  This results in : vlimit = (2 * G * M/dt) ^ 1/3
• rlimit is defined as: vlimit / dt

In each simultion the masses of the three objects are identified as m1, m2 and m3. The reference mass m0 is the mass of the Sun. m3 is the Single Stars. Figure 1 shows the configuration.

*m1 x x alpha x <--- ----------x-----------------------------------------------------*m3 x x x m2* Figure 1

In most simulations the two objects m1 and m2 are the binary stars. alpha is the angle between m1 and m2 and the main axis. In that case the simulation is performed for alpha going from 0 to 180 degrees in steps of 10 degrees.

1. The first simulation describes the situation where m1 = m0, m2 = m0 and m3 = 0.001 * m0
   distance between m1 and m2 = 10000 km, vlimit = 235484, rlimit = 4,78 ,delta t = 0,0000203 and revolution time = 12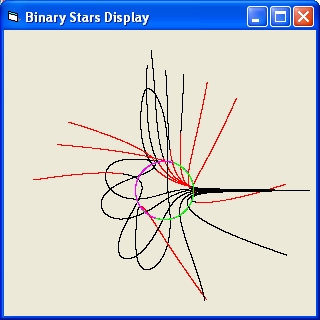

   Figure 2

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 0 3 653 9333 2592 2580 18328 2586 2580 4519 4675 10 3 136 9848 2614 2579 41932 2583 2579 6486 5102 20 2 3 10002 2600 2576 258151 2470 2576 258151 265222 30 3 194 9754 2580 2580 39091 2580 2580 6509 5312 40 3 599 9281 2581 2580 23261 2581 2580 5755 5310 50 3 1111 8778 2583 2580 17726 2583 2580 4892 5282 60 3 1638 8319 2583 2580 15034 2583 2580 3893 5171 70 3 2099 7903 2583 2580 13517 2580 2578 2091 4645 80 3 2438 7505 2583 2579 12565 2575 2576 792 4949 90 3 124 5547 2587 2586 47104 2562 2567 6847 5287 100 3 15654 25000 2576 2575 2929 2576 2575 2929 5249 110 3 15325 25000 2576 2575 2969 2576 2575 2969 5278 120 3 15184 25000 2576 2575 3009 2576 2575 3009 5293 130 3 15244 25000 2576 2576 3042 2575 2576 3042 5291 140 3 4041 7 2585 2678 187485 2568 2565 7726 5297 150 3 5610 468 2584 2583 23061 2567 2567 7709 5245 160 3 7451 949 2581 2583 15582 2573 2577 5964 4819 170 3 8523 1469 2580 2586 12201 2579 2581 1779 5280 180 3 9333 653 2580 2592 18328 2580 2586 4519 4675

   • Column 11 shows the escape velocity at the end of the simulation cycle.
   • Column 10 shows the speed of m3 at the end of the simulation. Certain numbers in that column are in red . The reason is that the final speed is higher than the escape velocity.
   • Column 1 shows the angle in increments of 10 degrees.
   • Column 2 shows the number of objects at the end of the simulation cycle. For angle 20 the number is two. That means m3 collided with m1 or m3. The final speed is also very large.
   • columns 3 shows the minimum distance between m3 and m1. For angle 20 the value 3 is very small that means m3 collided with m1
   • columns 4 shows the minimum distance between m3 and m2. For angle 140 the value 7 is very small that means m3 almost collided with m1
   • The collums 5, 6 and 7 show the maximum speed of m1, m2 or m3.
   • The collums 8, 9 and 10 show the speed of m1, m2 or m3 at the end of each simulation cycle.

2. The second simulation describes the situation where m1 = m2 = m0 and m3 = 0.001 * m0
   The distance between m1 and m2 = 1 AU = 149600000 km, vlimit = 1925, rlimit = 0,00047, revolution time = 22315464
   The masses of the stars selected is realistic. See List of massive stars

   Figure 3

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 0 3 0,065 0,933 21,19 21,09 149,85 21,14 21,09 36,94 38,22 10 3 0,013 0,984 21,37 21,08 342,83 21,12 21,08 53,02 41,71 20 2 0 1 21,26 21,06 2110,61 20,2 21,06 2110,61 2168,42 30 3 0,019 0,975 21,09 21,09 319,6 21,09 21,09 53,21 43,43 40 3 0,059 0,928 21,1 21,09 190,17 21,1 21,09 47,05 43,41 50 3 0,111 0,877 21,11 21,09 144,93 21,11 21,09 40 43,18 60 3 0,163 0,831 21,12 21,09 122,92 21,12 21,09 31,83 42,27 70 3 0,209 0,79 21,12 21,09 110,52 21,09 21,08 17,09 37,97 80 3 0,243 0,75 21,12 21,09 102,73 21,05 21,06 6,48 40,46 90 3 0,012 0,554 21,15 21,15 385,12 20,95 20,99 55,98 43,23 100 3 0,273 0,312 21,14 21,14 92,71 21,14 21,14 16,99 41,25 110 3 0,279 0,136 21,13 21,09 119,94 21,05 21,04 36,89 43,33 120 3 0,292 0,053 21,13 21,09 184,9 21,02 21 45,69 42,92 130 3 0,326 0,012 21,13 21,18 374,46 21 20,98 53,74 42,86 140 3 0,404 0 21,13 21,9 1532,85 20,99 20,97 63,17 43,31 150 3 0,561 0,046 21,12 21,12 188,55 20,98 20,99 63,03 42,88 160 3 0,745 0,094 21,1 21,12 127,4 21,04 21,07 48,76 39,4 170 3 0,852 0,146 21,09 21,14 99,75 21,08 21,1 14,55 43,17 180 3 0,933 0,065 21,09 21,19 149,85 21,09 21,14 36,94 38,22

3. The third simulation describes the situation where m1 = m2 = 100 * m0 and m3 = 0.5 * m0
   distance between m1 and m2 = 5984000 km, vlimit = 96264, rlimit = 2864,24, revolution time = 17852
   The masses of the stars selected is realistic. See List of massive stars

   Figure 3

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 0 3 113300 1628819 1090 1075 15137 1031 1037 3437 2560 10 3 675874 2344858 1065 1073 5976 1040 1034 2958 2481 20 3 1720968 3682166 1066 1068 3816 1049 1047 1098 2363 30 3 1054951 4913807 1072 1062 4526 1067 1062 779 2400 40 3 486069 5483155 1083 1058 6636 1069 1058 1933 2197 50 3 124789 5844170 1115 1055 13723 1057 1055 2846 2515 60 2 1525 5986932 1551 1053 102671 1551 1052 102671 131919 70 3 63865 5907657 1060 1056 21174 1051 1056 2937 2556 80 3 245573 5682892 1055 1057 11220 1054 1057 2686 2547 90 3 491499 5423305 1057 1058 8198 1057 1058 2411 2553 100 3 759536 5183228 1060 1058 6783 1060 1058 2125 2566 110 3 1012616 4970785 1063 1059 5997 1063 1059 1804 2571 120 3 1215778 4776583 1066 1060 5520 1066 1060 1393 2534 130 3 1341902 4585266 1067 1060 5210 1054 1056 161 2233 140 3 1381950 893236 1068 1060 5974 1045 1043 1943 2530 150 3 1355603 190866 1070 1063 12083 1039 1034 2589 2470 160 3 1319159 18324 1072 1126 38162 1038 1031 2955 2475 170 3 1363818 5022 1074 1265 73075 1038 1031 3203 2503 180 3 1628819 113300 1075 1090 15137 1037 1031 3437 2560

4. The fourth simulation describes the situation where m1 = m2 = 100 * m0 and m3 = 0.5 * m0
   distance between m1 and m2 = 149600000 km, vlimit = 19252, rlimit = 71606, revolution time = 2231546
   

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 0 3 2832507 40720485 218 215 3027 206 207 687 512 10 3 16896874 58621461 213 214 1195 208 206 591 496

   What the above table shows is that when you increase the distance with a factor of 25 that than the speeds decrease with a factor of 5. The revolution time increase with a factor of 125.

Answer Question 3 - Two binary stars and Blackhole ?

This simulation is identical as the one described above, That means starting point is a binary pair and a third star m3. The main difference is that the mass of m3 is not small but large: a Black Hole.
The main difference is that m3 will not move towards the binary pair but the binary pair will move towards the Black Hole.
The initial speed of the masses m1 and m2 is below the escape velocity (v = sqr(2*G*(m3)/R)) of the mass m3 of the Black Hole.
Accordingly to the document Sagittarius A our Galaxy contains a Black Hole of 4000000 Solar masses.

5. The fifth simulation is with m1 = m0, m2 = m0 and m3 = 100 * m0. That means the Black Hole m3 is small, like a large star.
   vlimit = 186904 and rlimit = 759,81

   Figure 5a alpha between 0 and 90

   Figure 5b alpha between 100 and 180

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 0 3 22106 5389 34474 69807 707 1471 1393 38 1940 10 3 34259 12235 27690 46317 472 1493 1353 38 1931 20 3 45930 19664 23912 36523 374 1511 1319 38 1922 30 3 56620 26930 21536 31200 321 1525 1290 38 1913 40 3 66434 33880 19881 27808 287 1536 1264 37 1905 50 3 75798 40699 18612 25363 262 1545 1241 37 1896 60 3 85190 47671 17556 23427 243 1553 1219 37 1887 70 3 94878 54955 16635 21812 226 1564 1200 37 1881 80 3 104645 62330 15840 20473 212 1582 1190 37 1881 90 3 113518 68926 15209 19463 202 1600 1182 37 1881 100 3 119657 73022 14815 18905 196 1617 1180 38 1881 110 3 120798 72117 14747 19024 196 1628 1185 38 1881 120 3 117341 63575 14964 20271 207 1631 1203 38 1881 130 3 427551 46096 9010 23831 239 1976 1039 31 1881 140 3 34194 22190 27711 34403 334 1444 1531 39 1883 150 3 13354 31354 44369 28887 435 2086 1024 41 1881 160 3 2314 1677 106556 125189 1241 1350 1541 39 1888 170 2 112 282125 408746 9632 4133 408746 7090 4056 1881 180 3 3169 17448 91042 38806 919 1415 1467 39 1943

   What the results show is that in three situations the final speeds are higher than the escape speeds. This implies HV stars.
   • In the case of alpha = 130 the final speed of the HV star m1 is roughly 100 km
   • In the case of alpha = 150 the final speed of the HV star m1 is roughly 200 km
   • The case of alpha = 170 m2 is the HV star. m1 collides with the Black Hole.
     This requires a more detailed investigation.

     Figure 5c alpha between 165 and 172

     angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 165 2 470 150177 214206 14344 2166 214206 5962 2077 1881 166 2 668 33909 162231 28467 1712 162231 5576 1557 1881 167 2 188 36254 206238 27466 2165 206238 6623 1987 1881 168 2 41 8685 214725 55351 2397 214725 7004 2066 1881 169 1 404 706 177875 168906 3240 177875 168906 3240 256056 170 2 225 21848 206805 34696 2250 206805 6737 1993 1881 171 2 355 91740 220252 17161 2280 220252 6592 2137 1881 172 2 507 196882 220422 12079 2247 220422 6149 2147 1881

     Figure 5c shows:
     • A purple line. This are 8 simultions of m1 which collides with the Black Hole. m1 always comes first.
     • 8 green lines which represent m2. One line green line counts for two simulations.
       • In the top 3 (4) lines (Alpha from 165 to 168) the star m2 starts from the left, moves above the Black Hole and towards the bottom. When the line turns black the speed is above the escape velocity.
       • The middle line (Alpha = 169) the star m2 also collides with the Black Hole.
       • In the bottom 3 lines (Alpha from 170 to 172) the star m2 starts from the left, moves below the Black Hole and towards the top. When the line turns black the speed is above the escape velocity.
       What this means is that in 7 cases there is a HV star.

6. The sixth simulation is identical as the fifth with both m1 and m2 equal to m0.
   The difference is that m3 = 1000 * m0
   vlimit = 300000, rlimit = 2949,17 and delta t = 0.000813

   Figure 6a alpha between 0 and 180

   angle n stars rmin 13 rmin 23 v1 max v2 max v1 v2 v3 v esc 0 1 2938 2924 296229 296834 397 296229 296834 396 300552 10 1 2932 2933 294321 294640 580 294321 294640 580 300826 20 1 2940 2881 295481 297280 541 295481 297280 541 300432 30 2 4614 2883 239859 298265 382 4365 298265 292 4206 40 2 9558 2882 166792 300872 319 3979 300872 297 4206 50 3 7172 4171 192264 252127 253 3330 3046 8 4206 60 3 9943 6353 163285 204274 205 3344 3034 8 4206 70 3 13499 9264 140128 169157 170 3360 3020 8 4206 80 3 18123 13160 120933 141913 143 3380 3003 8 4206 90 3 23921 18159 105257 120799 122 3402 2985 8 4206 100 3 30612 24027 93039 105006 106 3428 2968 8 4206 110 3 37321 29969 84258 94011 95 3455 2952 8 4206 120 3 42528 34566 78929 87530 88 3483 2942 8 4206 130 3 44371 36042 77272 85715 86 3511 2940 8 4206 140 3 41444 32960 79958 89637 90 3535 2948 8 4206 150 3 34571 25129 87552 102672 102 3550 2968 8 4206 160 3 15369 14239 131330 136424 135 3488 3070 8 4206 170 3 6973 19974 194995 115148 193 4332 2529 9 4206 180 1 2871 2830 300453 303029 343 300453 303029 296 304019

   What the above results show is that:
   • For alpha = 10 there is both a collision between m1 and the Black Hole and between m2 and the Black Hole
   • For alpha = 30 there is only a collision between m2 and the Black Hole. m1 is ejected as a HV star.
   • For alpha = 170 and alpha = 180 both m1 and m2 collide. In the simulation m1 is set to zero and the simulation continues as if nothing has happened. That is not realistic. The real solution is to improve accuracy.

   The second simulation is repeated for alpha between 160 and 180. The accuracy is improved with a factor 5.
   vlimit = 688560, rlimit = 559.83, delta t = 0.000813, revolution time 12195

   Figure 6b alpha between 160 and 180

   Figure 6c alpha 170 and 180

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 160 3 15369 14239 131330 136424 135 3488 3070 8 4206 162 3 14208 11983 136591 148723 147 3357 3212 8 4206 164 3 12375 9785 146362 164587 163 3115 3432 8 4206 166 3 10370 7699 159886 185554 182 2913 3848 8 4206 168 3 8576 6215 175834 206524 208 3050 3380 8 4206 170 3 6973 19974 194995 115148 193 4332 2529 9 4206 172 2 5642 1746 216768 389898 391 16426 16854 17 4206 174 3 4513 1630 242369 403929 405 3578 2976 8 4206 176 3 3555 1223 273091 467283 468 3229 3335 8 4251 178 3 2747 838 310702 566376 565 3354 2964 8 4206 180 2 2072 555 357698 653312 651 1990 653312 651 4206

   Figure 6b shows the result for alpha between 160 and 180
   Figure 6c shows the results for alpha = 170 and 180. The two top lines are for alpha = 170. The two bottom lines are for alpha= 180.
   • For alpha = 172 there is a collision between m1 and m2.
   • For alpha = 180 m2 collides with m3. m1 seems to be jected as a HV star, however the speed of m1 is too high. A more realistic interpretation is that both m1 and m2 collide with m3.
   • For alpha = 170 there is no collision and m1 is ejected as a HV star.
   • in all the other situations there is no collision but also no HV star. Both binary stars stay captured.
   The overall conclusion is that when the Black Hole has a mass of 1000 Suns it is possible that HV stars are ejected. However the speed of the HV star is just slightly larger as the escape velocity. (4300 versus 4200)

7. The seventh simulation is identical as the fifth with both m1 and m2 equal to m0.
   The difference is that m3 = 10000 * m0
   vlimit = 867531, rlimit = 3526.73 and delta t = 0.0040652

   Figure 7

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 0 3 15145 16627 418721 399547 42 7539 8173 2 10303 10 3 16135 17702 405589 387335 40 7538 8177 2 10303 20 3 16506 18106 401155 382802 40 7539 8173 2 10303 30 3 16670 18324 399074 380618 39 7540 8162 2 10303 40 3 16831 18534 397027 378447 39 7539 8149 2 10303 50 3 16982 18730 395275 376376 39 7537 8135 2 10303 60 3 17015 18808 395002 375632 39 7546 8136 2 10312 70 3 16769 18607 397974 377742 39 7553 8138 2 10318 80 3 16028 17908 407118 385038 40 7554 8135 2 10314 90 3 14526 16470 427731 401545 42 7552 8131 2 10303 100 3 11966 14116 471580 433570 47 7571 8151 2 10303 110 3 8097 12086 572808 469000 57 7598 8186 2 10303 120 2 3374 4035 843441 828941 94 843441 7975 83 10303 130 1 1407 3513 867118 717307 157 867118 717307 157 1373229 140 1 2607 3249 856269 759928 131 856269 759928 131 1008914 150 3 5787 5082 681576 736930 73 8113 7453 2 10303 160 3 10373 9253 506778 536996 53 8140 7583 2 10303 170 3 14157 12826 432981 455377 45 8167 7560 2 10303 180 3 16523 15045 400770 419994 42 8182 7551 2 10303

   In the case of a Black Hole with a mass of 10000 Sun masses:
   • For alpha = 120 m1 collides with the Black Hole.
   • For alpha = 130 and alpha = 140, in both cases, both m1 and m2 each collide with the Black Hole.
   • In all other cases there is no collision with the Black Hole. However there are no HV stars ejected, because the maximum speeds of the binary stars are too high. What the simulation in all cases should show is a collision of binary stars with the Black Hole ( rlimit should be larger)

The overall result is that it is not possible to simulate HV stars using a BH of 4 million sunmasses and a binary system.

Answer Question 4 - A black hole and two smaller stars

In this configuration the Black Hole (m1) and one stars (m2) forms the binary pair. This is identical as the stars identified in the document: Sagittarius A. The third star approaches this pair under the assumption that the initial speeds of the third star is below the escape velocity of the two binary stars (v = sqr(2*G*M/R)).

8. The eigth simulation describes the situation where m1 = 4000000 * m0, m2 = m0 and m3 = m0
   distance m1 and m2 = 1000 AU, vlimit = 1007050, rlimit = 0,00699, revolution time = 15,8 years.

   Figure 8

   3 1 2

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 350,6225 3 0,092 0,016 0,06 1922,51 277084,5 0,06 1922,44 277084,5 276345,24 350,623 3 0,181 0,011 0,04 1938,81 197520,3 0,04 1938,72 197466,26 197363,75 350,6235 3 0,508 0,006 0,02 1978,77 118120,38 0,02 1978,61 118117,99 118138,3 350,624 3 4,075 0,001 0,01 2229,56 41653,59 0,01 2228,45 41653,59 41728,35 350,6245 3 3,683 0,002 0,01 1940,58 43841,43 0,01 1674,5 43841,43 43896,96 350,625 3 0,47 0,007 0,03 1905,02 122782,48 0,03 1803,19 122781,3 122798,72

   Figure 8 Consists of 3 parts:
   • A center part, identified with the letter 1.
   • A bottom part, identified with the letter 2
   • A top part, identified with the letter 3
   Each part in principle shows the same simulations.
   • The center part is the most important. The BH m(1) is in the center. The star m(3) starts from the left and moves in a straight line towards the BH, assuming that m(2) is not available.
     The star m(2) is the green line. m(2) moves counter clockwise.
     When the initial angle is 350,6225 m(3) moves from the left towards the right just above m(2) which approaches from the bottom at close distance. With initial angle 350,623 the distance between the two pathes is closer. With 350,6235 the distance is even closer.
     The initial angle 350,624 shows the closest distance between m(3) and m(2), with m(3) passing above and before m(2). In that case the path of m(3) shows the largest bend towards the bottom. This case has also the largest negative influence on the speed.
     Starting from initial angle 350,6245 m(3) passes below m(2). The path of m(3) immediate also has the largest bend but now in the opposite direction. This case also shows the largests influence on the speed, but now in positif direction. (Gravity assist). However this increase is not large enough to escape from the Black Hole.
     Initial angle 350,625 also shows the same behaviour but less pronounced.
   • The bottom part shows a detail of the center part enlarged. This is the situation where m(3) and m(2) meet.
     m(3) moves from left to right and m(2) from the bottom towards the top
     There are 4 lines (difficult to see) which turn towards the bottom. The line with the largest bend represent initial angle 350,624.
     There are 2 lines which turn towards the top. The line with the largest bend represent initial angle 350,6245. In all those 6 situations the final figure will be an ellipse.
   • The top part shows a detail of the center part enlarged. This is the situation where m(3) meets m(1). In all the situations there is no collision. The simulation stops when m(3) is at closest distance to m(1).
     There are four lines which approach the black hole from the bottom. Those lines represent the intial angle 350,624 and smaller. The initial angle of 350.624 is the largest curve.
     There are two lines which approach the black hole from above. Those lines represent the intial angle 350,6245 and larger. The initial angle of 350.6245 is the largest curve.
     It should be mentioned that all the 6 pathes shown are an ellips.

9. The nineth simulation describes the situation where m1 = 4000000 * m0, m2 = 100 * m0 and m3 = m0
   distance m1 and m2 = 1000 AU, vlimit = 300000, rlimit = 0,07885, revolution time=15,8 years.

   Figure 9

   3 1 2

   angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 350,616 3 22,741 0,043 0,05 1894,25 17468,11 0,04 1894,15 17468,11 17665,47 350,618 3 670,818 0,024 0,04 1899,65 1965,28 0,04 1899,65 1965,28 3252,61 350,62 3 999,992 0,008 0,04 1916,3 3324,96 0,04 1883,24 1594,51 2540,03 350,622 2 1000,001 0,001 0,04 1932,74 7196,85 0,04 1932,74 7196,85 2664 350,624 3 717,718 0,009 0,04 1891,83 4875,89 0,04 1872,39 3368,21 2540,03 350,626 3 307,559 0,026 0,04 1887,86 4817,23 0,04 1868,96 4817,23 4803,64 350,628 3 132,053 0,045 0,04 1886,5 7203,58 0,04 1873,13 7203,58 7330,95

   Figure 9 has the same layout as Figure 8
   When you study the results with the initial angle of 350,622 there is a collision.
   
   • In three cases m(3) passes above m(2)
   • In three cases m(3) passes below m(2). In two cases m(3) becomes a HV star.

10. The tenth simulation describes the situation where m1 = 4000000 * m0, m2 = 100 * m0 and m3 = m0
    distance m1 and m2 = 10000 AU, vlimit = 73909, rlimit = 1.29927, delta t = 2630, revolution time=500 years.

    Figure 10

    3 1 2

    angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 325,432 3 419,278 0,148 0,01 603,04 4036,48 0,01 600,64 4036,48 4114,19 325,433 3 9999,95 0,056 0,01 609,43 1373,54 0,01 600,71 385,01 711,98 325,434 2 10000,011 0,019 0,01 607,22 1764,4 0,01 607,22 1764,4 842,43 325,435 2 9999,994 0,035 0,01 599,56 2476,86 0,01 593,31 2476,86 842,43 325,436 3 6508,622 0,115 0,01 597,42 1501,27 0,01 594,59 1053,32 738,54 325,437 3 3906,323 0,218 0,01 596,8 1433,22 0,01 590,41 1433,22 1347,88 325,438 3 2297,511 0,327 0,01 596,51 1773,81 0,01 591,62 1773,81 1757,54 325,439 3 1425,467 0,439 0,01 596,34 2220 0,01 592,36 2220 2231,29

    Figure 10 has the same layout as Figure 8
    When you study the results with the initial angle of 325,435 there is a collision.
    
    • In four cases m(3) passes above m(2)
    • In four cases m(3) passes below m(2). In three cases m(3) becomes a HV star.

11. The eleventh simulation describes the situation where m1 = 4000000 * m0, m2 = 20 * m0 and m3 = m0
    distance m1 and m2 = 300 AU, vlimit = 300000, rlimit = 0,07885, delta t = 2,277, revolution time=81992047 = 2,6 years
    This situation describes the three stars S2, S8 and S12 in the Central Blcak Hole in Sagittarius A. Those 3 stars create a circle with a radius of roughly 300 AU.

    Figure 11

    3 1 2

    angle n stars rmin 13 rmin 23 v1 max v2 max v3 max v1 v2 v3 v esc 325,435 3 12,553 0,002 0,02 3527,89 23328,19 0,02 3522,51 23328,19 23776,6 325,43525 3 15,869 0,002 0,02 3556,12 20619,11 0,02 3544,64 20619,11 21147,1 325,4355 3 15,385 0,001 0,02 3610,74 20952,66 0,01 3576,31 20952,66 21477,62 325,43575 3 299,999 0 0,01 3759,64 6397,78 0,01 3679,17 629,58 4110,65 325,436 2 300 0 0,01 3965,09 13764,43 0,01 3965,09 13764,43 4863,78 325,43625 3 264,987 0 0,01 3531,24 12875,96 0,01 3350,44 6776,82 4110,65 325,4365 3 155,824 0 0,01 3480,1 7588,51 0,01 3259,57 7588,51 6748,66 325,43675 3 80,192 0,001 0,01 3465,48 9563,63 0,01 3315,15 9563,63 9407,35 325,437 3 43,659 0,002 0,01 3458,55 12680,91 0,01 3343,31 12680,91 12749,54

    Figure 11 has the same layout as Figure 8
    When you study the results with the initial angle of 325,436 there is a collision.
    
    • In four cases m(3) passes above m(2)
    • In four cases m(3) passes below m(2). In three cases m(3) becomes a HV star.

Background and Historical Overview

The reason of this question started already in 1990 after reading the well written article "Black Holes in Galactic Centers" by Martin J.Rees, in Scientific American of November 1990.
In this article he writes at page 33 that:

"A good indicator of the presence of a black hole in our galactic center would be the existence of exceptional fast moving stars that had been accelerated away from the center by a gravitational slingshot".

At page 31 he writes:

"Slingshot ejection can occur when a binary star closely approaches a black hole. One star may be captured while the other escapes at up to 10000 kilometers per second. Normal encounters between stars cannot produce such velocities."

During that same period in 1991 I bought my first PC (a QL) and one of my first tasks was to try to simulate this effect. The problem was I failed.
Starting point was a simulation with three objects: Two objects at close distance and a third much heavier object ( a Black Hole ) at a certain distance. Initial condition of the binary pair was below the escape velocity.
After the start of the simulation the binary pair starts to move towards the Black Hole. The speed of the pair increases. The interesting part starts when the three objects meet.
During close encounter three things could happen:

• 1 star is ejected as result of the sling shot effect
• both stars are captured by the "Black Hole"
• 1 star or both stars collide with the Black Hole.

The result depents very much about one parameter: The mass of the Black Hole relative to the Binary Pair.

A factor of 100 was already too much

In the description with the program in 1991 I wrote:

• Combination 3 (BH = 10000, star=100, planet=0) does not show slingshot effect
• Combination 4 (BH = 500000, star=50, planet=0) does not show slingshot effect
• Combination 6 (BH = 10000, star=100, planet=100) closely resembles combination 3. No slingshot effect is observed

In the description I wrote:

Next I tried two stars of mass 50000 which form a binary star system and a planet which moves in its direction. The major angle is here the starting angle between the two stars. The slingshot effect exists for alpha between 15 and 45 degr. Maximum is at 40 degr.
This result is rather asthonising because they show that fast moving stars can be observed, however not caused by blackholes but by binary star systems.

In Scientific American of 1990 Martin J.Rees writes at page 33:

When a binary star passes close to a central massive black hole, one star may be captured into orbit about the hole while the other escapes at high speeds

The results of my simulations 1n 1991 and now show the same result:

This description is correct for small black holes. For large black holes there is always a collision with both stars.

He also writes at page 33:

Superfast stars ejected from the black hole acquire their kinetic energy at the expense of their former binary companions, which find themselves in orbits trapped deep within the hole's gravitational well. In addition to seeking superfast stars, astronomers might search for stars orbiting close to the galactic center at velocities in excess of 10000 km a second

Superfast stars are ejected from Black Holes but only for very small one's. The Black Hole within our Galaxy is too large.
There are stars observed circulating around the Black Hole in our Galaxy, but they are not superfast, nor the cause is not as described. See: Sagittarius A. They are trapped because there are more and probably heavy stars circulating around the black hole. Those stars cause other stars, which move towards the Black Hole in a straight line, to change direction and become like "commets" around the BH as described by the slingshot effect.

Background Part 2

In the document On the origin of the hypervelocity runaway star HD271791 by V.V. Gvaradmadze is written:

The existence of the HV stars was predicted by Hills in 1988, who showed that close encounter between a tight binary system and the supermassive black hole (BH) in the Galactic Centre could be responsible for ejection of one of the binary components with a velocity of up to several 1000 km per second

This is wrong IMO. The problem is that simulations show that in such a system the binary pair will always collide with the BH.
Next is written:

Yu & Tremaine in 2003 proposed and additional possible mechanism for production of HV stars based on the interaction between a single star and a putative binary BH in the Galactic Centre.

For more detail about binary BH see: Hypervelocity Binary Stars: Smoking Gun of Massive Binary Black Holes
In this Astrophysical Journal (ApJ) document is written:

In this Letter, we demonstrate that binary stars can be ejected out of the Galactic center with velocities up to 103 km s-1, while preserving their integrity, through interactions with a massive binary black hole. Binary stars are unlikely to attain such high velocities via scattering by a single massive black hole or through any other mechanisms.

It is true that HV stars can be explained by assuming a binary BH. The main question to answer is: is there a binary BH in our galaxy ? Aperently the answer is No.
It is interesting to read my vision in Appendix A "Our Galaxy" of the documentation in 1991:

It is my opinion that the center of our spiral Galaxy consists of 2(or/4) black holes which form a binary system and which move relative slowly around each other
Around those black holes are a cloud of stars which are pulled in first and the are ejected. In that way they can form the spiral arm. Galaxies with three spiral arms are caused by three black holes

Next in the document by Gvaradmadze is written:

HD271791 is the only HVS with measured proper motion and all measurements show that this star was ejected from the periphery of the Galactic disc.
There are two possible alternative explanations of the origin of HV Stars.
The first one is that the HV Stars attain their high peculiar velocities in the course of strong dynamical three- or four-body encounters in young and dense star clusters located in the Galactic disc.

If the authors mean a binary system composed of 3 or 4 objects mean, than such a system can eject HV Stars
Next is written:

The second one was proposed by Abadi, Navarro & Steinmetz in 2009. According to these authors, some HV Stars could originate from tidal disruption of dwarf galaxies during their close passage near the Milky Way.

A Dwarf galaxy as a single object is no general explanation for HV Stars. HV Stars can only be created as the result of a close encounter with a single object.
In paragraph 4 "Dynamical ejection scenario" is written:

The second basic mechanism responsible for the origin of runaway stars is based on dynamical three- or four-body interactions in dense stellar systems (Poveda et al. 1967; Aarseth 1974; Gies & Bolton 1986). Below, we discuss two possible channels for producing high-velocity runaways within the framework of the dynamical ejection scenario (cf. Gvaramadze 2009).

This is IMO the only correct solution which are supported by my simulations in 1991.

For a more updated ApJ document read this: The Anisotropic Spatial Distribution of HyperVelocity Stars
In that document we read:

Thus the 14 unbound 2.5-4 M0 stars found in the Brown et al. (2007b, 2008) targeted surveys are almost certainly HV Stars ejected from the Galactic center.

Unbound implies outside the gravitional attraction of Our Galaxy.
In paragraph 3 of that ApJ article is written:

While an equal-mass binary MBH is ruled out in the Galactic Center (Reid & Brunthaler 2004), theorists speculate that the massive star clusters in the Galactic Center form intermediate mass black holes (IMBHs) in their cores.

IMO this should be possible to observe as a ripple to the stars circulating in the center of Our Galaxy. It is important to consider that the speed of an IMBH should not exceed c. I have great doubts if such a pair can create unbound HV stars.
An other interesting earlier Apj article is this: Discovery of an unbound HyperVelocity Star in the Milky Way Halo

Feedback

Back to my home page: Contents of This Document