Quantum Factoring Performance Evaluation - Using Parallel Programming - VB2022
The purpose of this document is to evaluate system performance in order to factorize large numbers in two prime numbers using Parallel Computing
The CPU evaluated is an a Intel Core i5 1035G1 @1.00 Ghz (Quad Core)
The programming languages used is Visual Basic 2022. Parallel Processing is implemented using the BackGround Worker.
The Intel Processor used consists of four processors.
Each processor is capable to handle 4 parallel threads. That means the Intel Processor consists of eight threads or logical processors.
The name of the program is: "VB2022 FindPrim QC"
To perform the tests discussed in this chapter it is important that the PC does not go into sleepcondition.
Windows 10 - Select Configuration. Select System. Select Energy and sleep condition. Select Sleep condition net: Never.
The source file
The previous highest number (test 6) factorized using i5 M 460 was: 123018668531826302376221323
The two prime numbers are: 33478071698993 and 36746043666811 or roughly 10^27
Performance = 2153 seconds = 0 hours 35 min and 53 seconds
To perform that same test on a i5 1035G1 is 660 seconds = 11 min and 20 seconds
The current highest number, as of 19 july 2023, (test 8) factorized using i5 1035G1 and 4 Processors is:
123018668453224488047682618773 or roughly 10^29
The two prime numbers are: 334780716990043 and 367460436668111
Performance = 10047 seconds = 3 hours 47 min and 27 seconds
|
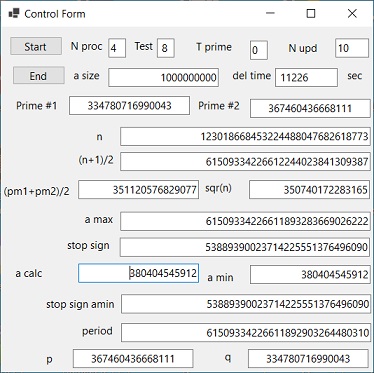 Picture 1a
VB2019 Test 8 CF
VB2019 Test 8 MF - Selected
Picture 1a
VB2019 Test 8 CF
VB2019 Test 8 MF - Selected
|
|
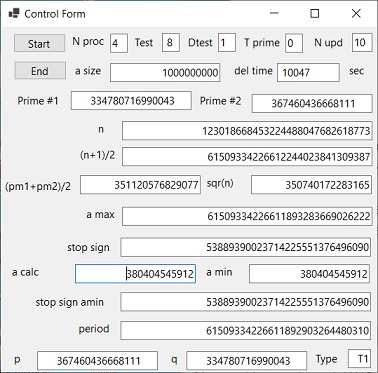 Picture 1b
VB2022 Test 8 CF
VB2022 Test 8 MF - Selected
Picture 1b
VB2022 Test 8 CF
VB2022 Test 8 MF - Selected
|
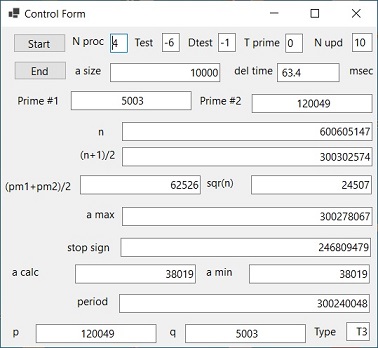 Picture 2a
VB2022 Test -6
Picture 2a
VB2022 Test -6
|
|
 Picture 2a
VB2022 Test -6
Picture 2a
VB2022 Test -6
|
- Picture 1A shows "Control Form" of program: "VB2019 Findprim QC" in order to do prime number factorization of Test 8.
When the Picture is selected the "Monitor Form" is displayed.
- Picture 1B shows "Control Form" of program: "VB2022 Findprim QC" in order to do prime number factorization of Test 8.
When the Picture is selected the "Monitor Form" is displayed.
The duration is smaller.
- Picture 2A shows "Control Form" of program: "VB2022 Findprim QC" to test the T2,T3 etc functionality.
When the Picture is selected the "Monitor Form" is displayed. This is important to demonstrate that this functionality also works with parallel processing.
For a detailed explanation of this functionality select: findprim_array_x.xls.htm Excel is used because excesive data has to be displayed.
Performance evalution
The following table shows the perfomance evalution to factorize large numbers of different sizes using one, two three or four processors.
Intel Core 1035G1 @1.00 Ghz
| Test | 0 | 1 | 2 |
3 | 4 | 5 | 6 | 8 |
| pm1 | 33478079 | 334780717 | 3347807173 |
33478071761 | 334780716989 | 3347807169919 | 33478071698993 | 334780716990043 |
| pm2 | 36746063 | 367460449 | 3674604371 |
36746043727 | 367460436671 | 3674604366743 | 36746043666811 | 367460436668111 |
| amin | 38041 | 380405 | 3804046 | 38040455 |
380404547 | 3804045461 | 38040454592 | 380404545912 |
| a size | 10000 | 100000 | 1000000 | 10000000 | 100000000 |
1000000000 | 10000000000 | 10000000000 |
| pp = 4 | 0,052 | 0,071 | 0,120 | 0,676 | 6,095 | 73,8 | 777 | 11226 |
|
Table 1: VB2019 FindPrim QC
Intel Core 1035G1 @1.00 Ghz
| Test | period | stop sign |
| 0 | 615093764914418 | 562856816646609 |
| 1 | 61509335941560384 | 89146125164832112 |
| 2 | 6150933432074270820 | 1787540236663610903 |
| 3 | 615093344377562888880 | 1101918085787451187506 |
| 4 | 61509334226553083574980 | 19498278967689246691067 |
| 5 | 6150933422795429791033578 | 4261854706813765918062172 |
| 6 | 615093342265878039130427760 | 1202674798664227559604492644 |
| 7 | 61509334226585966610859435500 | 52424584213408915799818872402 |
| 8 | 61509334226611893283669026222 | 53889390023714225551376496090 |
|
Table 1a: VB2022 FindPrim QC - stop sign
The following table shows the perfomance evalution to factorize large numbers of different sizes using one, two three or four processors.
Intel Core 1035G1 @1.00 Ghz
| Test | 0 | 1 | 2 |
3 | 4 | 5 | 6 | 8 |
| pm1 | 33478079 | 334780717 | 3347807173 |
33478071761 | 334780716989 | 3347807169919 | 33478071698993 | 334780716990043 |
| pm2 | 36746063 | 367460449 | 3674604371 |
36746043727 | 367460436671 | 3674604366743 | 36746043666811 | 367460436668111 |
| amin | 38041 | 380405 | 3804046 | 38040455 |
380404547 | 3804045461 | 38040454592 | 380404545912 |
| a size | 10000 | 100000 | 1000000 | 10000000 | 100000000 |
1000000000 | 1000000000 | 1000000000 |
| pp = 4 | 0,049 | 0,056 | 0,121 | 0,668 | 5,889 | 58,4 | 518 | 10047 |
|
Table 2: VB2022 FindPrim QC
In order to understand the program "VB2019 FindPrim QC" the user should study : Answer question 11 - Calculating Periodicity in 5 easy steps Specific study Example 4 and the concepts amax and amin. The difference between those two parameters is the period.
The Visual Basic "VB2019 FindPrim QC" program follows the same 5 steps.
- In test 2 the number to factorize n = 12301866871170953183 which consists of two prime numbers: pm1 = 3347807173
and pm2 = 3674604371. See Picture 2 below
Calculate (n+1)/2. This is 6150933435585476592
Calculate sqr(n). This is the number 3507401726
Subtract those two numbers. You get : 6150933432078074866. This is amax. This number is larger than the periodicity.
- Now calulate 2 ^ amax mod n or 2 ^ 6150933432078074866 mod 12301866871170953183.
You get : 1787540236663610903. This is the stop sign.
- Now calculate 2 ^ amin mod 12301866871170953183 = 1787540236663610903 (stop sign)
This is a "difficult" calculation. See below for more detail.
The value you should get is amin = 3804046
- Now subtract amin from amax. The value you get is 615093343274270820. That is the period.
Divide period by 2 or 615093343274270820 by 2. You get: 3075466716037135410. This is per2
Now perform 2 ^ per2 mod n or 2 ^ 3075466716037135410 mod 12301866871170953183. You get 3151404462955436851. This is y.
- Now perform GCD (y+1,n) and GCD(y-1,n). The results are the two prime numbers searched for.
However the last two steps can also be modified to get a much faster algorithm:
-
Add "amin" to sqsr(n). you get (pm1 + pm2)/2 = 3507401726 + 3804046 = 3511205772 = s/2
When you multiply this number by 2 you get pm1 + pm2 = s (sum)
You already have n. which is equal to n = pm1 * pm2.
- In order to calculate pm1 and pm2 to you to solve the following equation: (replace pm2 by pm)
- (s - pm)*pm = n or pm^2 - s*pm + n = 0
-
That means: pm = (s +- sqr(s^2 - 4 * n))/2 = s/2 +- sqr( (s/2)^2 - n)
You get pm = 3511205772 +- sqr(3511205772*3511205772 - 12301866871170953183)
and next = 3511205772 +- sqr(26699102155162801) = 3511205772 +-163398599
and finally pm1 = 3347807173 and pm2 = 3674604371.
The beauty of this algorithm is that you always get the correct result without any guessing.
What is also important is that GCD algorithm is not used.
|
"VB2022 FindPrim QC" Program source.
To try the program there is an executable available. To load this excutable as a Zip file goto: VB2022 FindPrim QC.zip
For more detail about how to operate the program use the above link.
VB2022 FindPrim QC Details
In order to understand product factorization using VB2022 FindPrim in more detail it is important to understand Test 7 using VB2019.
 Picture 3a
VB2019 Test 7
Picture 3a
VB2019 Test 7
|
|
 Picture 3b
VB2022 Test 0
Picture 3b
VB2022 Test 0
|
|
 Picture 3c
VB2022 Test 7
Picture 3c
VB2022 Test 7
|
|
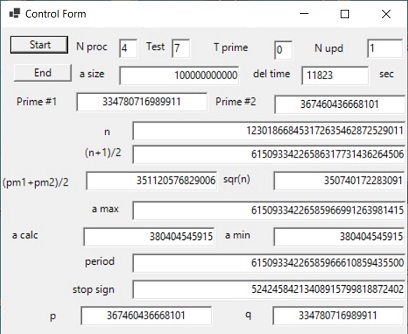
Picture 3a shows the factorization of n = 123018668453172635462872529011. However both the two prime numbers and the duration of 11823 seconds are wrong.
Test 7 uses the two prime numbers 334780716989911 and 367460436668101
These two prime numbers are each part of the following sequence of prime numbers:
| 334780716989819 |
334780716989821 | | 33478071698983 | 334780716989863 | 334780716989893 |
334780716989903 | * | 334780716990043 | 334780716990053 | 334780716990107 |
| 367460436667967 | 367460436667969 | ** | 367460436668111 | 367460436668137 | 367460436668183 |
367460436668201 | | 367460436668231 | 367460436668249 |
However when you look at position * the prime number 334780716989911 and at position ** the prime number 367460436668101, both are missing.
The above values are calculated using the Excel program: find_prim_x.2.benchmarkx.xls
The only conclusion can be: The two prime numbers used in Test 7 are wrong
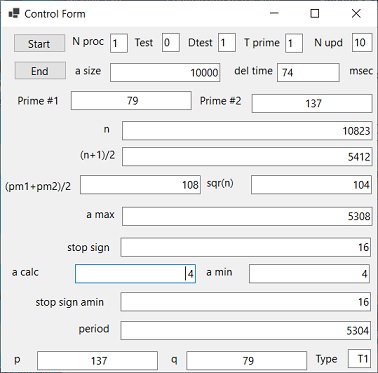
To investigate the reason consider Picture 3b. This shows the factorization of n = 10823, which the product of the two prime numbers 79 and 137.
Five calculations are important:
- The first involves the period calculation which uses amax, amin
amax is calculated as: amax = (n+1)/2 + sqr(n) = 5308
amin is the same as acalc. acalc is calculated as: acalc = amin = (pm1+pm2)/2 - sqr(n) = 108 - 104 = 4
The period calculation is: period = amax - amin. In this example period = 5308 - 4 = 5304
- All the following calculations involve Modular 2 Exponention in the form of: 2^a mod n = xn
The second calculation is the amax stop sign calculation: 2^amax mod n = 2^5308 mod n = 16.
- The third calculation is the amin stop sign calculation: 2^amin mod n = 2^4 mod n = 16.
- the fourth calculation is: 2^ period mod n = 2^ 5304 mod n = 1
- The fifth equation is: 2^amax mod n = (2 ^ amin mod n) * (2^ period mod n) or 2^5308 mod n = (2 ^ 4 mod n) * (2^ 5304 mod n) or 16 = 16 * 1
The issue is that the equations 2,3 and 4 can be performed before the calculation of amin and are a test that this calculation will succeed.
In that case the print output (with the Debug.Print statement) of the subroutine Main_Int shows:
- Test 0 with n=10823
Main_Int 1 Modular_2_exp_Int_array 2^amax mod n = 2^5308 mod 10823 = 16
Main_Int 2 Modular_2_exp_Int_array 2^amin mod n = 2^4 mod 10823 = 16
Main_Int 4 Modular_2_exp_Int_array 2^period mod n = 2^5304 mod 10823 = 1 Should be 1
In Test 0 with n=10823 the two stop signs when a=amax and when a=amin are the same.
-
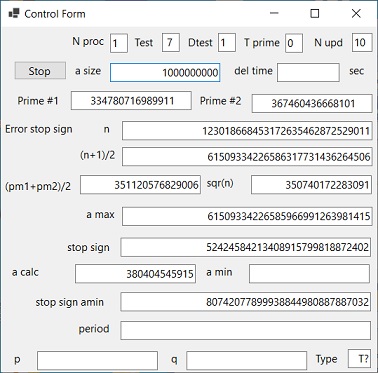
With Test 7 the printer output shows:
trace 11 pm1 334780716989911 pm2 367460436668101
Main_Int 1 Modular_2_exp_Int_array 2^amax mod n = 2^61509334226585966991263981415 mod 123018668453172635462872529011 = 52424584213408915799818872402
Main_Int 2 Modular_2_exp_Int_array 2^amin mod n = 2^380404545915 mod 123018668453172635462872529011 = 80742077899938844980887887032
Main_Int 4 Modular_2_exp_Int_array 2^61509334226585966610859435500 mod 123018668453172635462872529011 = 59345945384029708177592406792 Should be 1
In Test 7 the two stop signs when a=amax and when a=amin are different.
-
Test 8
trace 11 pm1 334780716989903 pm2 367460436668111
Main_Int 1 Modular_2_exp_Int_array 2^amax mod n = 2^61509334226586171053102258526 mod 123018668453173043586549083233 = 45974955432214577569296125968
Main_Int 2 Modular_2_exp_Int_array 2^amin mod n = 2^380404545916 mod 123018668453173043586549083233 = 45974955432214577569296125968
Main_Int 4 Modular_2_exp_Int_array 2^61509334226586170672697712610 mod 123018668453173043586549083233 = 1 Should be 1
In Test 8 the two stop signs when a=amax and when a=amin are the same.
Maint_Int is the subroutine executed after the "Start push button" is selected, part of the program "VB2019 FindPrim QC".
Historical overview
The document VB2019 shor-findprim-QC.htm has an important message: With the "VB2019 FindPrim QC.sln" program it is possible the factorize the example identified as Test 7. Not only that: with that program it is possible to factorize any product of two prime numbers. However this result was to optimistic. Implementing the same algorithm using Visual Studio 2022 as "VB2022 FindPrim QC.sln" showed that that program did not work. What went wrong.
In order to understand are the subroutines Geta_mod_Int_array and Geta_mod2_PP which are used to calculate amin. Geta_mod2_PP is functional identical as Geta_mod2_Int_array, but uses parallel processing. Execution time of Test 7 is roughly 3 hours.
The program consists of a loop with "a" going from 1 to amax (in principle).
-
Before the the loop is executed the following two statement are performed: a = 1 and xn = 2
Within this loop 3 calculations are performed:1) a = a + 1 and 2)xn = xn * 2 and 3) if xn>n then xn = xn -n
The loop is terminated when xn = stop sign. At that moment amin = a.
The problem with Test 7 is, that at the moment when a is equal to amin then xn is not equal to stop sign.
That means when a = 380404545915 then xn = 80742077899938844980887887032 which should be 52424584213408915799818872402
To establish that acalc is used, which is the predicted value of amin, when xn = stop sign.
To make that vissible on the program display we use the Debug.Print statement which displays (prints) the two values a and xn, starting with a = acalc - 3 untill a = acalc + 3. The problem is that the moment amin = a is reached after approx. 3 hours, xn = is not equal to 52424584213408915799818872402 but to 80742077899938844980887887032.
The result is that the loop is not terminated and continues untill the program is manual terminated (which is difficult)
To investigate the reason is tricky, because as mentioned it takes 3 hours to reach this moment.
To speed up this moment a special parameter is added to the program Geta_mod2_PP called a0 to initialize a. Normally this value is 0. When you set a0=380000000000 or a0=380400000000 this will do the trick.
The question can be raised if there is nothing
to warn in advance, that something is wrong. The answer is yes. Like you can calculate the stop sign at amax using modular 2 exponentation, you can also calculate the stop sign at acalc, which is the predicted value of amin. Both these stop signs should be equal.
The predicted period, which is the difference between amax and acalc (amin), can also be tested.
Both these can be used in advance if amin can be calculated and factorization will work.
The conclusion is that the origin of that Test 7 uses two prime numbers which are no prime numbers.
The problem arises because Test 7 uses two predefined numbers which were supposed to be prime numbers, but are not. To solve that the parameter Control_Form.TTprime.Text should have been set to 1. "T Tprime" means "Test prime numbers".
What this means that there is nothing wrong with the factorization algorithm used.
However still there is a problem. The problem is that Picture 3a shows a solution, which seems to be correct, but it is not. Something is wrong with the software.
To investigate what is wrong two test are performed:
- One test identical as Test 0, with pm1 = 33478079 and with pm2 36746063. This test is used to demonstrate factorization of two prime numbers.
The results are shown in Table 3A and Table 4A.
- And a second test with pm1 = 33478079+2 and with pm2 = 36746063+2. This test is used demonstrate factorization of two odd numbers, identical as Test 7.
The results are shown in Table 3B and Table 4B. (Both should indicate an error)
And this with two programs:
- One with the original program "VB2019 FindPrim QC" as used in Test 7 picture 3A. The results are in Table 3A and 3B.
- One with a corrected version of "VB2019 FindPrim QC". This is the same as "VB2022 Findprim QC".The results are in Table 4A and 4B.
pm1 33478079 pm2 36746063 n 1230187600052977
Main (pm1+pm2)/2 35112071 sqr(n) 35074030 amin 38041 amax 615093764952459
period 615093764914418 Stop sign 1
Stop sign amax 562856816646609 Lc 50 9 764952459
Stop sign amin 562856816646609 Lc 16 9 38041
Geta_mod2_PP Start 0 xval 562856816646609
Geta_mod2_PP Start 0 n 1230187600052977
Geta_mod2_PP np 1
Geta_mod2_PP 5 a 38041 lxn 2 ln 2 n 1230187600052977 xn 1793044416699586
Geta_mod2_PP 6 a 38041 lxn 2 ln 2 test 1 xn 562856816646609
Geta_mod2_PP 7 a 38041 0 1 cnt 42 xn 562856816646609 str_xval 562856816646609
Geta_mod2_PP 8 FinishedSt pr_end 1 test 0 np 1
Geta_mod2_PP 9 FinishedSt pp1 38041 pp2 0 pp3 0 pp4 0
Geta_mod2_PP 10 FinishedSt aa(2) 0 38041 pr_end 1 np 1
type? y p 36746063 q 33478079 Dtime 0.12512460000289138 125 msec
|
Table 3A
FindPrim QC 8-8-2021
prime numbers 33478079 and 36746063
|
pm1 33478081 pm2 36746065 n 1230187740501265
Main (pm1+pm2)/2 35112073 sqr(n) 35074032 amin 38041 amax 615093835176601
period 615093835138560 Stop sign 822998510771711
Stop sign amax 1029155177293882 Lc 50 9 835176601
Stop sign amin 523600715693967 Lc 16 9 38041
Geta_mod2_PP Start 0 xval 523600715693967
Geta_mod2_PP Start 0 n 1230187740501265
Geta_mod2_PP np 1
Geta_mod2_PP 5 a 38041 lxn 2 ln 2 n 1230187740501265 xn 1753788456195232
Geta_mod2_PP 6 a 38041 lxn 2 ln 2 test 1 xn 562856816646609
Geta_mod2_PP 7 a 38041 0 1 cnt 42 xn 523600715693967 str_xval 523600715693967
Geta_mod2_PP 8 FinishedSt pr_end 1 test 0 np 1
Geta_mod2_PP 9 FinishedSt pp1 38041 pp2 0 pp3 0 pp4 0
Geta_mod2_PP 10 FinishedSt aa(2) 0 38041pr_end 1 np 1
type ? y p 36746065 q 33478081 Dtime 0.11905409999599215 119 msec
|
Table 3B
FindPrim 8-8-2021
Odd numbers 33478079+2 and 36746063+2
|
pm1 33478079 pm2 36746063 n 1230187600052977
Main (pm1+pm2)/2 35112071 sqr(n) 35074030 acalc 38041 amax 615093764952459
period 615093764914418 Mod 2 Expo 1 SHOULD BE 1
trace 11 pm1 33478079 pm2 36746063
Main_Int 1 Modular_2_exp_Int_array 2^615093764952459 mod 1230187600052977 = 562856816646609 = a
Main_Int 2 Modular_2_exp_Int_array 2^38041 mod 1230187600052977 = 562856816646609 = a
Main_Int 4 Modular_2_exp_Int_array 2^615093764914418 mod 1230187600052977 = 1 Should be 1
Main_Int Step 5 stop sign : 562856816646609 xn5(1) 1 str_xn5$ 1
Geta_mod2_PP Start 0 xval 562856816646609
Geta_mod2_PP Start 0 n 1230187600052977
Geta_mod2_PP np 1
Geta_mod2_PP 6 a 38041 lxn 2 ln 2 test 1 xn562856816646609
Geta_mod2_PP 7 a 38041 0 1 cnt 42 xn 562856816646609 str_xval 562856816646609
Geta_mod2_PP 8 FinishedSt prn_end 1 test 0 np 1
Geta_mod2_PP 9 FinishedSt pp1 38041 pp2 0 pp3 0 pp4 0 prn_end 1
Geta_mod2_PP 10 FinishedSt aa(2) 0 aa(1) 38041pr_end 1 np 1
type ? y p 36746063 q 33478079 Dtime 0.19318809999822406 193 msec
|
Table 4A
FindPrim QC 26-7-2023
prime numbers 33478079 and 36746063 |
pm1 33478081 pm2 36746065 n 1230187740501265
Main_Int Step 3a acalc : 38041 amin predicted = (pm1+pm2)/2 - sqr(n)
Main (pm1+pm2)/2 35112073 sqr(n) 35074032 acalc 38041 amax 615093835176601
Main_Int Step 4 amax : 615093835176601
period 615093835138560 Mod 2 Expo 822998510771711 SHOULD BE 1
Main_Int 1 Modular_2_exp_Int_array 2^615093835176601 mod 1230187740501265
= 1029155177293882 = a
Main_Int 2 Modular_2_exp_Int_array 2^38041 mod 1230187740501265 = 523600715693967 = a
Main_Int 4 Modular_2_exp_Int_array 2^615093835138560 mod 1230187740501265
= 822998510771711 Should be 1
Geta_mod2_PP Start 0 xval 1029155177293882
Geta_mod2_PP Start 0 n 123018740501265
Geta_mod2_PP np 1
Geta_mod2_PP 6 a 38041 lxn 2 ln 2 test 1 xn 523600715693967
Geta_mod2_PP 7 a 38041 -1 1 cnt 42 xn 523600715693967 str_xval 1029155177293882
Geta_mod2_pp 40000
|
Table 4B
FindPrim QC 26-7-2023
Odd numbers 33478079+2 and 36746063+2 |
Table 3A
The result of Table 3A, with the original "VB2019 FindPrim QC" program, is as expected.
This program is used to perform the Test 0 until Test 6. The problem comes with Test 7, Picture 3A.
The reason why the algorithm works, is when using the prime numbers 5 and 13, 2^amax mod n and 2^amin mod n are calculated, the results are the same. In this case amax = 25, amin = 1, n= 65, 2^25 mod 65 = 2 and 2^1 mod 65 = 2.
Table 3B
The result of Table 3B, with the original "VB2019 FindPrim QC" program, is not as expected.
The reason why the algorithm does not work, is when using the odd numbers 7 and 15, 2^amax mod n and 2^amin mod n are calculated, the results are not the same. In this case amax = 43, amin = 7, n= 105, 2^43 mod 105 = 23 and 2^7 mod 105 = 2.
Table 4A
The result of Table 4A, with the "VB2022 FindPrim QC" program, is as expected.
This program is used to perform the Test 0 until Test 6. The problem comes with Test 7, Picture 3A.
The reason why the algorithm works, is when using the prime numbers 5 and 13, 2^amax mod n and 2^amin mod n are calculated, the results are the same. In this case amax = 25, amin = 1, n= 65, 2^25 mod 65 = 2 and 2^1 mod 65 = 2.
Table 4B
The result of Table 4B, with the "VB2022 FindPrim QC" program, is as expected: it indicates an error
The reason why the algorithm does not work, is when using the odd numbers 7 and 15 (15 is not a prime number), 2^amax mod n and 2^amin mod n are calculated, the results are not the same. In this case amax = 43, amin = 7, n= 105, 2^43 mod 105 = 23 and 2^7 mod 105 = 2.
The present situation - as of 5 August 2023
As of to day the program "VB2019 FindPrim QC.exe" works as expected, but the program "VB2022 FindPrim QC.exe" not.
Infact there are two problems:
The first is a problem with release 17.6.5 of Visual Studio 2022. See "Help". See "About Microsoft Visual Studio".
The major problem is the Debug.Print statement, in order to show the progress. This statement does not work in the "Debug" mode.
The second problem that in order to follow of flow of the program additional message lines have to be added, which is a horrible exercise.
How ever a much more serious problem is to detect errors in the complicated software as demonstrated above. The main reason is that special integer array subroutines are used.
The advantage of a PC is when the same program is executed again the same errors will pop up.
In the Quantum Computer, most probably is prone to the following errors:
- Errors in the Hardware related to the stability issues of Qubits.
- Errors in the logic primarily to calculate the Period.
IMO, in a QC there is an additional problem: When the same program is executed again, there is no quarantee that the same error will pop up.
First I would like to make a comment. At of this moment it is not clear to me how any application on a QC is implemented.
- On a PC this is done by writing a software program.
- On an analog computer this is done by building your application by means of a patch board. (As far as I remember)
- On a hybrid computer consisting of a digital computer and an analog computer it is software for a DC and a patch board for the analog part.
- On a hybrid computer consisting of a digital computer and a QC, I expect, it is software for a DC and a patch board for the QC.
The advantage in a PC is that all the intermediate results in a calculation leading to a software error can be displayed.
These messages will be repeated when the same program is repeated and will change when the program is modified and corrected (as expected).
IN a QC this predictability does not exist, specific when the application is implemented on a hybrid system, as explained above in #4. That means there are 3 causes of problems: In the program part of the DC, in the hardware of the QC and in the application build via the patch board on the QC.
This means when the output is not as expected you don't know what the cause is. This could lead to a program modification in the DC while the cause was in the QC hardware or with the usage of patch board.
Feedback
None
Created: 6 June 2023
Updated: 4 August 2023
Back to Shor's Algorithm - 10 Questions
Back to my home page Contents of This Document


