Program "Performance" Benchmark Pentium P4 2.8 and Intel i5 M 460
Visual Basic, Visual Studio 2010 and Excel
The purpose of this document is to evaluate a package of subroutines written in different programming languages necessary to factorize large numbers in two prime numbers
The subroutine package consists of two types of logic: Integer (Array) and (Double Precision) Array
For Integer Array logic the following subroutines are tested:
-
Mul_Int_Array, Div_int_Array, Sqr_Int_array, GETPRIEM_Int_array and FERMAT_Int_array
-
For Double Precision Array logic the following subroutines are tested:
-
Mul_Array, Div_Array, Sqr_array, GETPRIEM_array and FERMAT_array
-
The three different programming languages are: Excel, Visual Basic 5.0 and Visual Studio 2010.
The two CPU's evaluated are (1) a Pentium P4 and (2) a Intel Core i5 M 460 @ 2.53 Ghz.
The mathematical package is used to factorize large numbers. See: findprim benchmark
To evaluate factorization using Parallel processing select the following link:
-
Quantum Factoring Performance Evaluation - Using Parallel Processing - VB2010
-
General Performance Evaluation - Program "Performance"
The three programs evaluated are: Performance.xls, VB2010_Performance and VB_Performance.
- Performance.xls is a program written in Excel Basic
Source Excel program: performance.xls.zip
- VB_Performance is a program written in Visual Basic 5.0
"VB Performance.exe" file of program: VB exe.zip
- VB2010_Performance is a program written in Visual Basic 2010
"VB2010 Performance.exe" file of program: VB2010 exe.zip
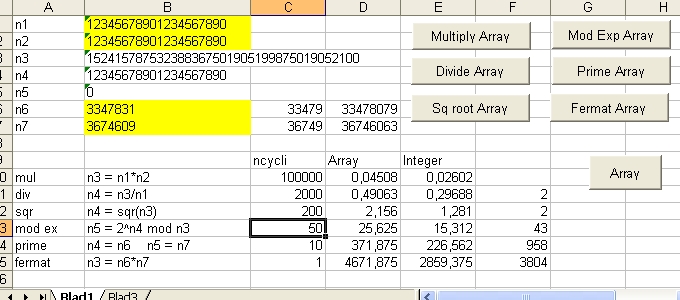
Excel Basic Benchmark
"Blad1" contains 5 Operation Commands:
- Multiply to test multiplication of n1*n2. The result is stored in n3.
- Divide to test division of n3/n1. The result is stored in n4. The remainder in n5
- SQR Root to test Square Root of n3/n1. The result is stored in n4. The remainder in n5
- Prime to test the nearest prime # of n6 and n7. The result of n6 is stored in n4. The result of n7 is stored in n5
- Fermat to test Fermat theorem of n6 and n7. First n6*n7 is calculated and the result is stored in n3. The two prime numbers are stored in n4 and n5
"Blad1" also contains the selection command "Integer" or the command "Array".
- When the "Integer" command is selected the command changes into "Array". The names of the 5 "Operation Commands" also change into "Array"
- When the "Array" command is selected the command changes into "Integer". The names of the 5 "Operation Commands" also change into "Integer"
Pentium P4
| Mul | 100000 | 0.04766 | 0.02594 |
| Div | 2000 | 0.5000 | 0.28906 |
| SQRoot | 200 | 2.265 | 1.406 |
| Mod 2 Exp | 50 | 26.25 | 16.562 |
| Get Prime | 10 | 376.562 | 229.687 |
| Fermat | 1 | 4671.875 | 2859.375 |
|
Intel Core i5 M 460 @ 2.53 GHZ
| Mul | 100000 | 0.06929 |
0.06152 |
| Div | 2000 | 0.705 | 0.560 |
| SQRoot | 200 | 3.046 | 2.304 |
| Mod 2 Exp | 50 | x | x |
| Get Prime | 10 | 535,156 | 376,953 |
| Fermat | 1 | 6492,1875 | 4621,093 |
|
Table 1: Performance.xls |
What Table 1 shows is that:
- That Pentium P4 is roughly 30% faster than Intel i5 processor.
- That Integer Array logic is faster than Double Precision Array Logic.
Visual Basic 5.0 Benchmark
Operation of the Control Form is almost identical as the Excel Benchmark
Pentium P4
| Mul | 100000 | 0.01093 | 0.00625 |
| Div | 1000 | 0.21875 | 0.13281 |
| SQRoot | 100 | 0.703125 | 0.625 |
| Mod 2 Exp | 50 | 8.4375 | 6.5625 |
| Get Prime | 20 | 212.5 | 96.875 |
| Fermat | 1 | 1765.625 | 1062.5 |
|
Intel Core i5 M 460 @ 2.53 GHZ
| Mul | 100000 | 0,02265 | 0,01093 |
| Div | 1000 | 0.36328 | 0.19921 |
| SQRoot | 100 | 1.953125 | 1.015625 |
| Mod 2 Exp | 50 | 21.5625 | 10.78125 |
| Get Prime | 10 | 322.6563 | 153.125 |
| Fermat | 1 | 4140.625 | 1734.375 |
|
Table 2: VB 5.0 Performance |
In the above benchmark for the Commands Multiply, Divide and Square Root the numbers n1 = n2 = 12345678901234567890 and
n3 = 152415787532388367501905199875019052100 are used
For the Commands Mod Ex, "Get Prime" and Fermat the prime numbers n5 = 3347831 and n6 = 3674609 are used
When you compare the results of Table 1, Table 2 and Table 3:
- That the Pentium P4 is the fastest CPU compared with the Intel Core i5 when only one processor is used.
- That Visual basic 5.0 outperforms Visual Studio 2010.
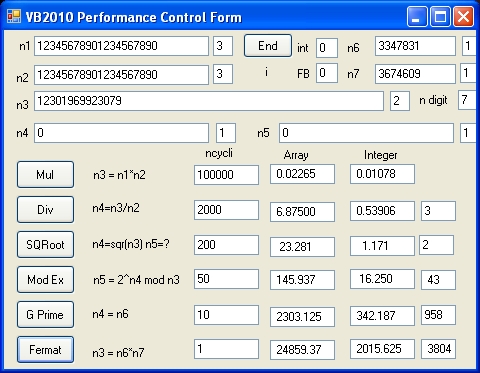
Visual Studio VB2010 Benchmark
|
The display shows the following functions:
| Mul | n1=12345678901234567890. n2= n1=12345678901234567890.
n3=n1*n2 = 152415787532388367501905199875019052100 |
| Div | n3= 152415787532388367501905199875019052100 n2 =12345678901234567890.
n4=n3/n2= 12345678901234567890. n5 = remainder = 0 |
| SQRoot | n3= 152415787532388367501905199875019052100
n4=Sqr(n3) = 12345678901234567890. n5 = remainder = 0 |
| Mod Ex | n6=3347831 n7= 3674609 n3=n6*n7 =12301969923079 n4=n6=3347831
n5= 2^n4 mod n3 = 3674609 |
|
Operation of the Control Form is almost identical as the Excel Benchmark
Pentium P4
| | Array | Integer |
Mul | 100000 | 0.02265 | 0.01078 |
| Div | 1000 | 6.73437 | 0.53125 |
| SQRoot | 100 | 22.812 | 1.406 |
| Mod 2 Exp | 50 | 144.687 | 16.875 |
| Get Prime | 1 | 2248.437 | 335.937 |
| Fermat | 1 | 25109.37 | 2031.250 |
|
Intel Core i5 M 460 @ 2.53 GHZ
| | Array | Integer 7 | Integer 9 |
Mul | 100000 | 0.03343 | 0.00530 | 0.00520 |
| Div | 1000 | 8.06653 | 0.5850 | 0.5600 |
| SQRoot | 100 | 27.170 | 1.400 | 2.000 |
| Mod 2 Exp | 50 | 172.201 | 18.700 | 18.000 |
| Get Prime | 10 | 2667.903 | 363.400 | 353.600 |
| Fermat | 1 | 29188.09 | 2006.003 | 1985.003 |
|
Table 3: VB2010 Performance |
What Table 3 shows is that:
- That Pentium P4 is roughly 30% faster than Intel i5 processor.
- That Integer Array logic is faster than Double Precision Array Logic.
- That Intel i5 processor outperforms Pentium P4 in case of Integer Array Logic
Subroutine Div_Int_Array
rem = A(In)
Div=A(Div)
A(Quotient) = zero
Do
tempin = rem/Div
A(temp) = tempin
A(Quotient) = A(Quotient)+A(temp)
A(in2) = A(Quotient) * A(Div)
A(rem) = A(in) - A(in2)
rem = A(rem)
Loop until tempin < 1
|
The program uses the following arrays: A(in),A(Div),A(Quotient),A(rem),A(temp) and A(in2)
The numbers: rem,Div and tempin are double precision floating point numbers.
|
Feedback
None
Created: 21 September 2015
Back to my home page Contents of This Document