|
|
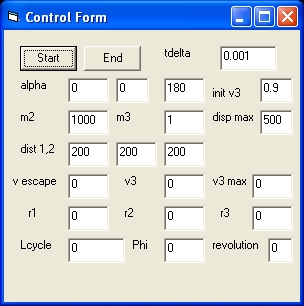
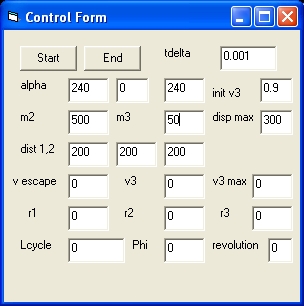
This dispay shows 3 Commands: Start, End and Stop. This depends about were you are during program execution.
- The Start command is used to start the program
- The End command is used to terminate the program
- The Stop command is used to stop the simulation
- tdelta shows the step size. The standard value is 0.005
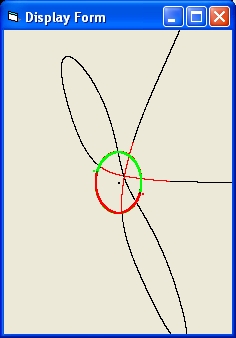
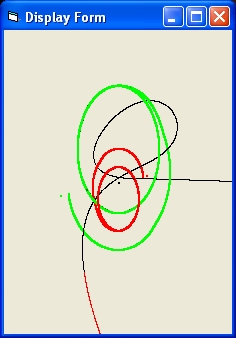
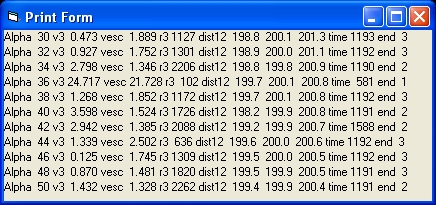
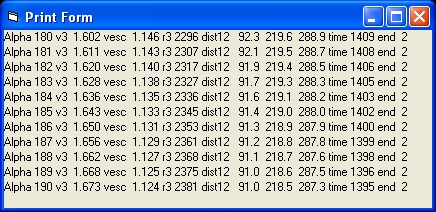
- The parameter alpha shows three values: the initial value, the average value and the final value in degrees of the angle between m1 and m2.
Only the initial value at the left and the final value at the right can be modified. - m2 is the mass of m2. The mass of m1 = 1000.
- m3 is the mass of m3. The standard value = 1
- init v3 initial fraction of the speed v3 versus the escape velocity. Standard value is 0.9
- disp max display size divided by 2.
Because the initial distance of m2 is 500 in the x direction the standard vale is also 500.
- v escape is the actual escape velocity of m3
- v3 is the actual velocity of m3
- r3 is the actual distance of r3 from the center of the binary stars
- Lcycle is the actual number of iterations or program cycles in the simulation
- Phi is the actual angle between m1 and m2
- revolutions is the actual number of revolutions of