Our Galaxy and the movement of planet Mercury

Question 1	How many theoretical revolutions around the Sun will the major axis (aphelion) of the planet Mercury make, during one revolution of the Sun around our Galaxy.
Question 2	Is "General Precession" important for the movement of Mercury when the Sun moves around our Galaxy
Question 3	How many revolutions around the Sun will the major axis (aphelion) of the planet Mercury actual make, during one revolution of the Sun through our Galaxy ?
Question 4	If you want to simulate this path is there length contraction involved ?
Question 5	If you want to simulate this path are there moving clocks involved ?
Question 6	If you want to simulate this path is variable mass involved ?
Question 7	What is the most important explanation that the path of the aphelion of Mercury is a horseshoe orbit ?

Purpose

Introduction - Question 3

The following picture consists of two parts

1. The left part shows the movement of the Sun through our Galaxy
2. The right part shows the movement of Mercury around the Sun in 1969. This is the start date of the simulations.

           <----  
             77                   			
           s     s             
        s         . s            
      s          .     s                <--
  |  s          .       s  ^             m  (perihelion)                      
  | s          .   phi   s |          m     m  
  |167        O.........347|        m    S    m        
  | s                    s |     | m           m ^       
  V  s                  s  |     | m           m |             
      s                s         V m           m |          
        s            s              m         m             
           s      s                   m     m
             257                         m  (aphelion)          
            ---->                       -->  
 O = Centre of Our Galaxy           S = Sun
 S = Sun                            m = Mercury 
                    Figure 1

The Sun moves in the direction of the arrow. Left side of "Figure 1". Speed is 250km/sec
In order to answer the question how the long axis behaves 4 simulations of 7 planets around the Sun are performed at different positions (identified by the angle phi) of the Sun within our galaxy. The four selected values of phi are 77 degrees, 167 degrees, 257 degrees and 347 degrees.
The results can be seen by selecting the targets 77, 167, 257 and 347 in the above picture.
The initial day of the simulations is 28 June 1969. This day comes from the book "Explanatory Supplement to the Astronomical Almanac" page 304, which supplies initial conditions in x,y,z coordinates. At that day the direction of the long axis makes an angle of roughly 257 degrees in the x y plane. This is the position drawn in the right hand picture.

The results of the 4 simulations is sumarized in the following table.

phi	77	167	257	347
angle 2000	257,56	257,54	257,55	257,56
angle 6000	264,93	262,17	262,08	264,68
forward angle 2000	522,19	416,90	540,74	650,67
forward angle 6000	662,97	416,64	409,24	640,91
avg distance 2000	57966339	57886872	57805080	57884565
avg distance 6000	68283161	58452925	46699031	57077919

1. The row "angle 2000" shows the angle of the aphelion at year 2000.
2. The row "angle 6000" shows the angle of the aphelion at year 6000.
3. The row "forward angle 2000" shows the forward angle in arc sec per century of the aphelion between 1969 and the year 2000.
4. The row "forward angle 6000" shows the forward angle in arc sec per century of the aphelion between 1969 and the year 6000.
5. The row "average distance 2000" shows the distance of the major axis divided by 2 of the year 2000.
6. The row "average distance 6000" shows the distance of the major axis divided by 2 of the year 6000.

The difference between the 4 simulations is quite remarkable.

• If you test 347 than you will see that both the forward angle and the average distance are quite constant. Both values very slowly decrease.
• If you test 167, which is at the opposite site, than you will again see that both the forward angle and the average distance are almost quite constant, but very slowly increase. The most important difference between the two are the forward angles. If you add the two values for the year 6000 you get 1057.55 If you divide this value by 2 you get: 528.72 which is close to the value of 529.6 you get when no speed of gravity is included. See here: Mercury simulatie in 3D
• If you test 77 , which is at the top, than you will see that both the forward angle and the average distance both slowly increase. The forward angle increases with roughly 140 arcsec/century
• If you test 257, which is at the bottom, than you will see that both the forward angle and the average distance slowly increase. The forward angle decreases with rougly 130 arcsec/century

Answer question 1

The (theoretical) total time for one revolution of the long axis of the planet Mercury is: 360/(574.1/3600) centuries = 2257 centuries or 225745 years.
The (theoretical) total number of revolutions of the long axis of the planet Mercury during one revolution of the Sun through our Galaxy is 200000000/225745 = 886
This number assumes that the shift is constant.

Answer question 2

"General precession" is explained in Precession
"General precession" is identical with precession of the equinoxes or precession of the equator. The total time for one revolution of axis of the earth is: 360/(5025.645/3600) = 257 centuries or 25788 years.
The concept "General precession" is of no importance in order to simulate the movement of the planet Mercury, because the planet Earth is considered a point sized object. The same for all the objects involved. However the concept "General precession" is important to convert Earth based observations into galatic coordinates inorder to calculate the positions of the Sun and the planets at a given instant.

Answer question 3 - v Milky way = 0

In this paragraph the movement of the planet Mercury is studied assuming that the speed of the Milky Way is zero.

• One of the posiblities is, that the path of the movement of the aphelion of the planet Mercury follows, what is called a horseshoe orbit. See "Figure 2"

  ^ | |S S = Sun 6 x | x 3 x x | 4 m x x x m x 5 m 7 2 x m x m 1a m 1b Figure 2

  The following table shows the angle, distance and year at the different positions. point angle distance year 1a 257 58000000 2000 1b 270 55000000 10000 2 303 9000000 36000 4 270 4700000 38000 5 201 15000000 41000

  For more details horseshoe orbits see: Wikipedia & Planetoide 3753 Cruithne and Paul Wiegert & Planetoide 3753 Cruithne

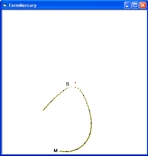
  In order to understand this let us start at position 347 in "Figure 1"

  • The direction of the Sun is straight up. The initial position of Mercury at aphelion is drawn as position 1 in "Figure 2"
    
  • Starting from position 1 the angle at aphelion will slowly increase. First position 2 and next position 3, where the long axis almost will be horizontal.
    
  • The question is will this movement continue.
    
  • In order to answer that question study "figure 3" below:

         ^             ^     /      \
         |             |    /        \
         |^            |<---3         --->
         ||            |.              ^
        / |           / .  2           |  
       /  |          /  .              |
          1\            1              3\
            \                            \
      pos 1            pos 2         pos 3
                     figure 3
    

    "Figure 3" consists of 3 positions of both your hands.
    1. pos 1 is equivalent of "figure 1" position 347.
       The left upper arrow is your left hand and this represents the movement of the Sun.
       The right upper arrow is your right hand and this reperents the long axis of planet Mercury. Number 1 (hand joint) is the aphelion.
    2. Turn your right hand counter clock wise. (See pos 2). This represents the movement of the long axis. The aphelion will go through the points 1, 2 and 3. This are the same points 1,2 and 3 as in "Figure 2"
    3. Move both hands 90 degrees clock wise. (See pos 3) and compare this with "figure 1" position 257. The two are the same. The hand at the top points towards the right and represent the movement of the Sun. The hand at the bottom shows the direction of the long axis.
       
    In short when your initial position is position 347 and when the aphelion moves forward 90 degrees this is equivalent with a movement of the Sun going backwards towards position 257.
  • If you observe the behavior of position 257 you will see that the distance will start to decrease and the aphelion will reach position 4 in "Figure 2".
  • To observe what happens next you have to select the following simulation: 7 planets simulation . This is a simulation over a period of 275000 years
    
  • From position 4 the aphelion will start to move backward to position 5 and 6. Position 6 is equivalent to position 77 in "figure 1". After position 6 the distance will start to increase to position 7. Position 7 is equivalent to position 167 in "figure 1". The angle at aphelion will increase again until the initial position 1 is reached.
  • The total revolution time of one aphelion movement is roughly 160000 years. The nearest point is after roughly 84000 years. The closest distance is than 4000000 km which is much more than the radius of the sun as approximate 700000 km.

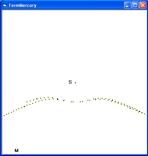
  In short the answer on question 3 is one, assuming that the horseshoe orbit of the aphelion moves synchronuous with the movement of the Sun. This is only a prediction.

• If you start from position 77 the path is also a horseshoe orbit.

  5 m m 6 4 m m m m m m m m S m m S = Sun <------ 7 3 m m 8 m x m x m 1a 2 m m 1b m m Figure 4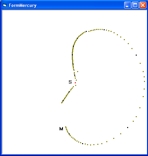

  The following table shows the angle, distance and year at the different positions. point angle distance year 1a 257 58000000 2000 1b 270 73000000 8000 2 325 90000000 15500 3 360 91000000 18000 4 405 85000000 22000 5 450 56000000 36000 6 457,4 23000000 51000 7 360 4000000 56000 8 457,4 8900000 58000

• If you start from position 257 the path is also a horseshoe orbit.

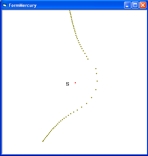
  x x x 4 m m 3 m m S S = Sun 2 ------> m m m m 1 Figure 5

  The following table shows the angle, distance and year at the different positions. point angle distance year 1 257 58000000 2000 2 180 7000000 17800 3 90 4000000 18000 4 74 50000000 30000

• If you start from position 167 current expectation is that the path is also a horseshoe orbit.

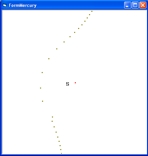
  | | |S S = Sun | V 3 1 m 4 2 m m 5 10 6 7 m 9 m 8 Figure 6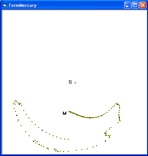

  The following table shows the angle, distance and year at the different positions. point angle distance year 1 257 58000000 2000 2 270 61000000 13000 3 333 86500000 34400 4 332 91000000 36200 5 321 11000000 42200 6 300 113000000 46600 7 297 122000000 50000 8 270 128000000 52800 9 245 132000000 58000 10 204 124000000 65600

• In short the answer there are three possible answers on question 3:

  1. one, assuming that the horseshoe orbit of the aphelion moves synchronuous with the movement of the Sun.
  2. many, assuming that the path is an ellipse.
  3. unknown, assuming that Mercury will collide with the Sun. This can happen when the initial position is between 77 and 167 for example at 127 degrees or when the initial position is between 167 and 257 for example at 207 degrees.

Answer question 3 - v Milky way is non 0

In this paragraph the movement of the planet Mercury is studied in relation to reference frame of the Cosmic Microwave Background radiation.

The North pole of the galaxy Galactic coordinate system.

• The Right Ascesion is 12h 51m and 26.282s The Declination is 27d 7m and 42.01
• The ecliptical longitude L is 180d 1m and 21.5s and ecliptical latitude B is 29d 48m and 39.8s.
  

In order to do the conversion from equatorial to ecliptical coordinates you can use: Astro Java
The Center of the galaxy Milky way is in the direction of Sagitarius A*.

• The Right Ascesion is 17h 45m and 40.04s The Declination is -29d 00m and 28.1s.
• The ecliptical longitude L is 266d 50m and 19.6s and ecliptical latitude B is -5d 32m and 13.7s.
  

The Sun is moving towards the direction of the star Vega.

• The Right Ascesion is 18h 36m and 56.336s The Declination is 38d 47m and 01.291s.
• The ecliptical longitude L is 285d 18m and 49.1s and ecliptical latitude B is 61d 43m and 55.5s.

In the reference frame of the "Cosmic Microwave Background Radiation" the Milky Way is moving with a speed of 552 km/sec towards the direction of Hydra.

• The Right Ascesion is 10.5 h The Declination is -24d.
• The ecliptical longitude L is 169d 20m and 0.1s and ecliptical latitude B is -30d 48m and 45.8s.

Figure 7A: Ecliptic plane

Figure 7B: Galactic plane

Figure 7B resembles point 77 in "Figure 1". However and that is important the direction V is the opposite. The result is that the precession will be less than 531 degrees.

Answer question 4

If you want to perform a simulation six steps are important:

1. First you need a model or a set of differential (difference) equations which describe the movements of the objects you want to simulate. This can be Newton's Law or General Relativity (GR).
2. Next you need a set of observations which describe physical parameters of the objects involved at different moments in time.
3. Next you need a set of transformations to transform the observations into the parameters of the grid i.e. of the model.
4. You need a set of initial conditions of the differential equations and you have to recalculate those initial conditions using the model, the parameters and the observations.
5. You need a set of initial values of the parameters of the differential equations and you have to recalculate those parameters using the model the initial conditions and the observations.
6. And Finally: Transformation of the coordinates of the calculations (The 3D grid) to the coordinates of the observations. This is where precession is taken in to account. The same with light travel time, moving clocks and light bending by mass.

• Step 4, 5 and 6 have to performed many times until the error between the results of the simulation and the observations becomes 'Zero'.
• There are also constraints involved. If the distance between two objects becomes too close, a collision takes place and the two objects merge in one.

Answer question 5

Special Relavity studies the behaviour of moving clocks, specific what is called Relativity of Simulataneity
The simplest way to explain Relativity of Simulataneity is the following:

1. Consider a moving train and a track. There are two observers one near the track and one on the moving train.
2. Two lightning bolts hit the train and the track (almost ?) at the same moment each. They each leave two markings both on the train and the track.
3. As it happens when the train stops, both, the observer near the track and on the train are standing at equal distance between the two markings at respectivily near the track and on train.
4. Chances are that the Observer near the track will claim that he saw the two flashes simultaneous. The observer at the train in that case will claim that he did not see them simultaneous.
   This is easy to explain because the observer at the track will claim that he met the observer at the train "in the past" and not when he saw the two flashes simulataneous "at a later moment", because the train with the observer moved away. This is what is called Relativity of Simulataneity
5. There is also a chance that the Observer at the train will claim that he saw the two flashes simultaneous. The observer at the track in that case will not claim that he saw them simultaneous.
   The explanation is that the observer at the train will claim that he met the observer at the track "in the past" and not when he saw the two flashes simulataneous "at a later moment" because as a matter of speaking "the track with the observer moved away". This is also: Relativity of Simulataneity

1. Consider one observer who stands at a moving train in the middle of two mirrors. Suppose he turns on a lamp, which transmits two lightsignals, which are reflected by two the mirrors. This reflection defines two events. The observer will always see those lightsignals simultaneous, independent of the speed of the train.
2. The question is are those two events always simultaneous events? The issue is see versus are. IMO it does not make sense always to answer: Yes.
3. The same problem exists with the lightning flashes or bolts in the above example. Are those lightning bolts simultaneous events ? IMO only in one special occasion.
4. What makes the above example with the two observers even more complicated is that there is length contraction involved. When the moving train stops and when the distance between the two marks (caused by lightning) is measured it should be longer (accordingly to SR) than the length of the distance between the two marks near the track.
5. The reason is because when the lightning strikes at that moment the distance (length) between the markings on the track and on the train should be identical. However (accordingly to SR) a moving ruler is subject to length contraction, compared to a ruler at rest. This again means that when the train stops it should increase in size. The result is an increase in distance between the markers on the train.

Answer question 6

As far as I can see the masses of the objects involved are constant.
This is definitively the case if Newton's Law is considered as the model to perform the simulations. In fact in order to predict the future based on the past observations, first the masses of the objects have to be calculated, under the assumption that each is constant and that the total number of objects did not change. Collisions between objects can be considered, assuming that the total mass before and after is also the same.
Special Relativity uses the concept of a rest mass. This is the mass of an object at rest (v=0) within the coordinate system. IMO if you perform a simulation within the galaxy rest frame none of the masses involved are at rest. As such I expect that within GR the concept of rest mass is not used, in order to describe the movement of objects.

---

Answer question 7

What is the reason that the aphelion of Mercury follows a horseshoe orbit ?

• The most important reason is that the movement of the Sun (around in our Galaxy) is taken into account.
• If you want to simulate the movement of the Sun around the centre of our Galaxy than the "classical form" of Newton's law is sufficiant which assumes that gravity acts instantaneous. The speed of the centre of our Galaxy is considered zero.
• The model used to simulate the movement of the planets starts from the "classical form" of Newton's Law. This model is modified to include the effect that gravity does not act instantaneous. The result is that the gravity field of the Sun is not symmetric, as considered from the center of the Sun.
• In the "classical form" of Newton's law the gravity field from the Sun acts instantaneously and comes from the centre of the Sun. The forward angle is explained as an influence by the outer planets. In case Mercury moves towards the Sun this influence diminishes, which explains why the forward angle will decrease.
  If you assume differently than gravity comes from a point which represents the position of the Sun in the past. In the case of Mercury, which is an ellipse this point will vary, because the distance to the Sun also varies. This explains why the forward angle will vary more.

Reflection

In Wikipedia we read about relativity of simultaneity the following:

The observer onboard the train sees the front and back of the traincar at fixed distances from the source of light and as such, according to this observer, the light will reach the front and back of the traincar at the same time.

This demonstration very much resembles the situation as described above with the single observer except that the readers from Wikipedia get a complete wrong message. What is not drawn are the reflections from the front and the back and that is what the observer sees. The real questions to answer is are the two moments that the light hits the front and the back two simultaneous events.
Near the drawings there is also the remark: length contraction not depicted . Apparently for the authors this is an issue, but what the consequences are (if they know which) is not mentioned.

In the bibliographis record by Albert Einstein: 9. The Relativity of Simultaneity we read:

Are two events (e.g. the two strokes of lightning A and B) which are simultaneous with reference to the railway embankment also simultaneous relatively to the train ?

This raises the question: How do you know that two events are simultaneous ?

What makes the two documents so remarkably is that the two are so differently, while they try to explain the same concept. The Wikipedia document starts from one event which results in two simultaneous events, independent of the speed of the train. The A. Einstein document starts from two (simultaneous) events which results one event (observation) if the observer stands in the middle.

One concept used is what is called rest frame. A rest frame is a frame in which the speed of the observer is zero. The observer at the track is in a rest frame if his speed v = 0. The observer at the moving train is also in a rest frame (of the moving train) if he stands still (v = 0) in the train.
The important question to answer is: Are the trajectories of moving objects (Stars and planets) dependent of any such rest frame with an observer at rest. IMO the answer is: No. Moving Objects in space have nothing to do with the human concept of a rest frame nor with the human concept of simultaneous. Moving Objects are influenced by only by each other. Newton's Law assumes (in its original form) that this influence acts instantaneous. In the simulations this is not assumed. The transport mechanism are gravitons.

See also the following Usenet discussion: How important is SR/GR inorder to calc the precession of Mercury

Feedback