Friedmann's Equation & The path of a light ray

Contents

• Background - Excel program Friedman's Equation.xls
• Technical Information part1 Calculation Lightray Path
• Technical Information part2 redshift, z and delta l/l
• Reflection part 1 The path of a lightray since the Big Bang
• Reflection part 2
• Reflection part 3 - Question 7
• Reflection part 4 - Question 6 Calculation H0
• Reflection part 5 Visible Universe, Observable Universe, the horizon problem and the parameter age
• Reflection part 6 Linear space expansion - Milne's model
• Feedback Discusion Groups
• Literature

Background - Excel program Friedman's Equation.xls

The purpose of the questions 1-4 is to discuss the path of a light ray that is transmitted very close to the moment of the big bang and that reaches the eye of a present day observer.
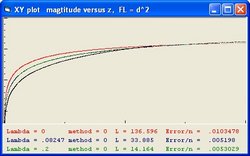
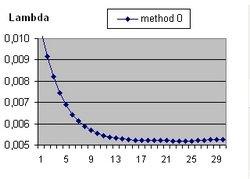
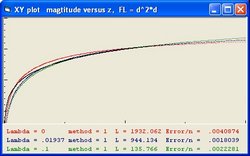
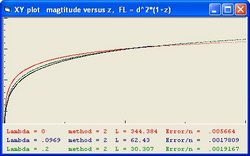
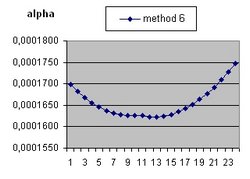
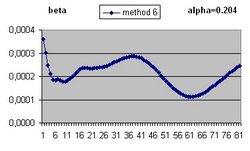
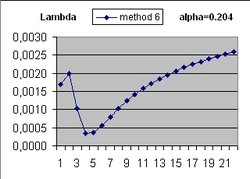
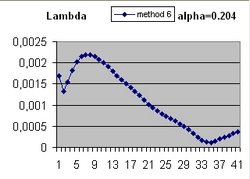
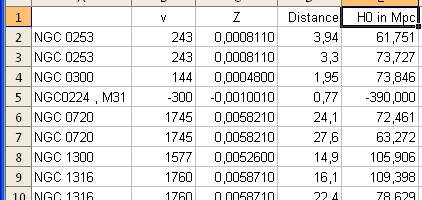
To answer these question the Excel program Friedmann's Equation.xls is used. The program simulates the Friedmann Equation.
To get a copy of the program and how to operate select: Operation Excel program friedmann's equation.xls & Copy

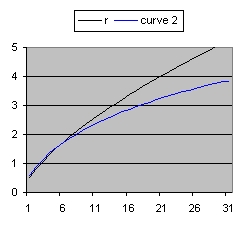
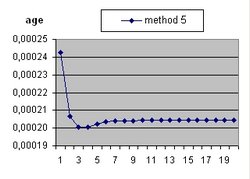
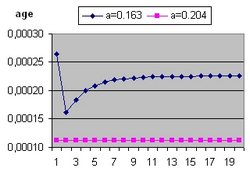
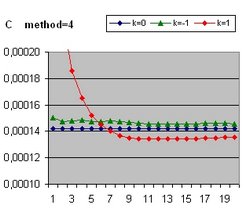
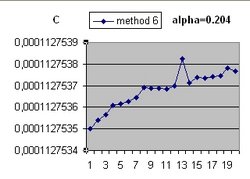
The age of the Universe is considered 14 billion years. This is also the value of parameter "age".

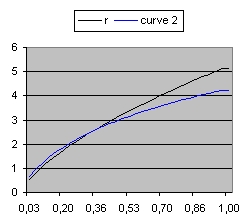
In order to simulate space expansion the Friedmann equation is used:
(See "Introducing Einstein's Relativity" by Ray d'Inverno. Equation 22.58 and 23.1

(dR/dt)^2= C/R + 1/3 * Lambda*R^2 - k

With flat space (k = 0) we get:

dR/dt = SQR ( C/R + 1/3 * Lambda*R^2 )

This is implemented as:

R(t) = R (t-1) + SQR ( C/R + 1/3 * Lambda*R^2 ) * dt

With: R(1) = v0 * dt

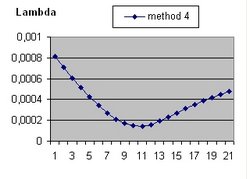
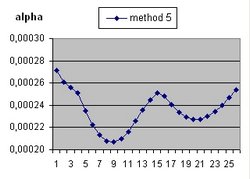
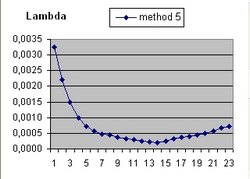
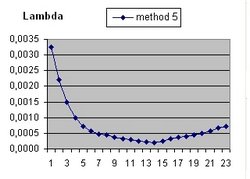
It should be understood that the parameter Lambda used in this document and the parameter Omega(Lambda) used in the Questions 11 and 13 are different parameters.

To understand the above equation better start from the first equation after : Friedmann equations - Wikipedia and replace both c and G with 1. You get than:

((da/dt)^2 + k) /a^2 = (8*pi*Rho + Lambda)/3

Next:

(da/dt)^2 + k = (8*pi*Rho/3)*a^2 + 1/3*Lambda*a^2

Replacing 8*pi*rho/3 by C/a^3 gives the above quation.

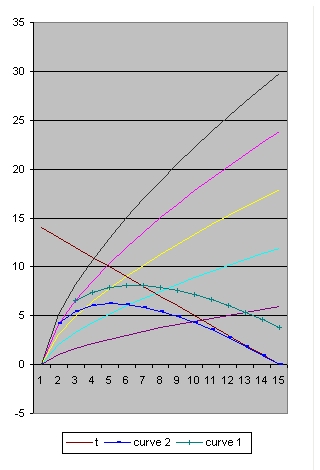
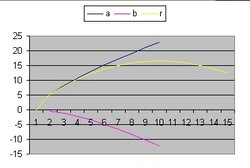
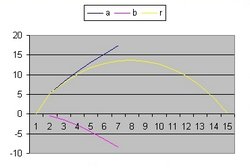
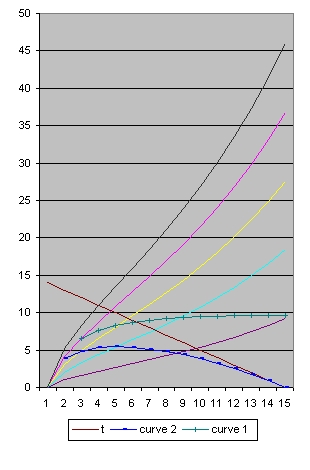
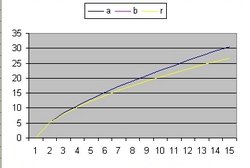
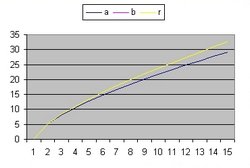
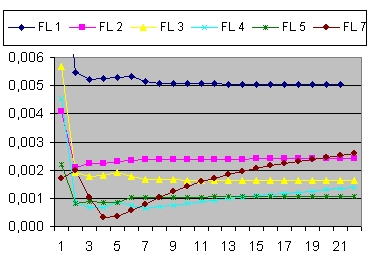
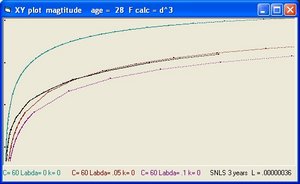
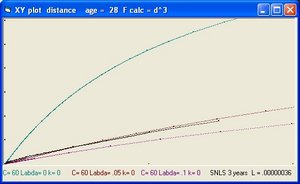
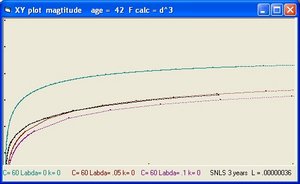
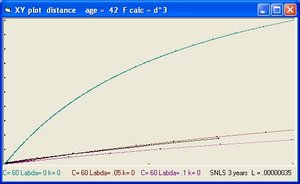
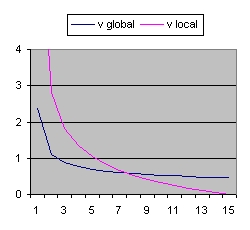
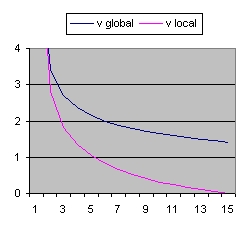
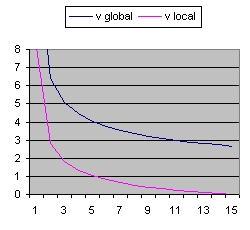
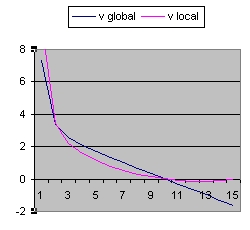
In addition to R(t) also two additional functions are implemented: a(t) and b(t)

• The function a(t) is the function R(t) with Lambda = 0 and is implemented as:
  a(t) = a(t-1) * SQR( c/R ) * delta t
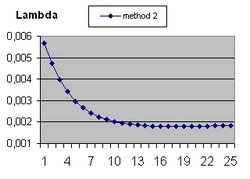
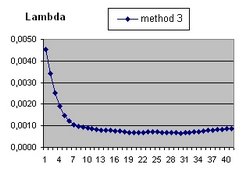
  The curve "b" is considered to simulate acceleration and is of the form:

  b(t) = b(t-1) * SQR( 1/3 * Lambda*R^2 ) * delta t

C = 60 Lambda = 0 v0 = 3 Figure 1

C = 60 Lambda 0.03 v0 = 3 Figure 2

In the above two pictures:

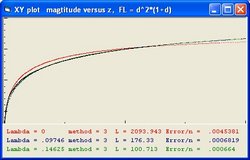
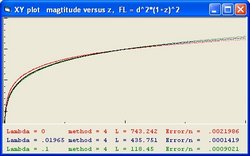
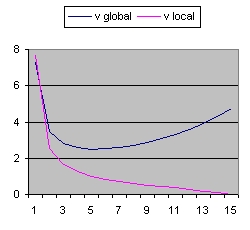
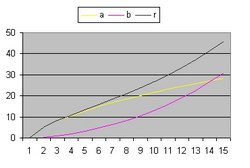
• The "Black" line is the function r(t). This function shows the total size of the Universe and is also called the 100% line.
• The "Yellow" line is the function a(t). This line shows the size of the Universe when Lambda = 0.
• The "Pink" line is the function b(t). This line shows the influence of the cosmological constant Lambda.

Answer question 1 - Lambda = 0

In the following picture the size of the Universe is drawn vertical in one dimension for 5 different situations:

at 100 % , at 80%, at 60% at 40 % and at 20%.

Space expansion is considered homogeneous and isotropic. See Wikipedia:Cosmological principle
The results are 5 lines which starts at t = 0 in one point (The Big Bang) and which are equally spaced at each instant t. The right side is considered the present: t = now.

C = 60 Lambda = 0 v0 = 3 Figure 3

Figure 4 Detail Figure 4 shows the detail of Figure 3 in the range of 0 to 1 billion years in 30 steps. That means 1 step is roughly 33 million years. The black line represents the 100% distance line. The blue line shows the light ray starting as close as possible near the Big Bang which reaches the Observer now. Figure 3 shows the condition when C=60. In order to study what happens when C=2 select this link: Figure 5: Friedmann C=2

At each picture, in addition to those 5 lines, there are three more lines:

a brown line, a green line and a blue line.

• The brown line starts from the left and moves towards the right bottom at t = 0 at an angle of 45 degrees.
  The brown line represents the path of a light ray, moving through space towards the observer along the x axis, at the speed of light assuming no space expansion is involved.
  The brown line can also be used from the point of view of the Observer in the opposite direction as a trace in the past of the path of the light ray.
  When space expansion is considered the shape of the brown line changes.
• The green line represent the path of a light ray originating at t = 2 billion light years at a distance of 80% of the size at that moment, including the influence of space expansion.
  Without space expansion the green line should follow a straight path parallel to the brown line. With space expansion the green line follows a line above that straight path.
  • The left picture shows that the green line will not reach the observer at present but later. The reason is that there is too much space expansion. The green line passes the brown line.
• The blue line represents the history of the light ray that reaches the observer at present.
  • The left picture shows that the light ray almost originates from the Big Bang at x = 0
  • The right picture shows the details of the first one billion years and shows that the light ray originates at roughly 300000 years after the Big Bang. That is the point where the blue line crosses the black line or 100% line.

The following table shows the most important results of the simulations for three different values of C: 2, 60 and 400.
The First Column shows the time in billion of years, or the distance along the x axis in billion of light years.

t BB 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 - - - - - -

C = 2 r blue v z 0,00 0,00 11,089 25,842 1,65 4,24 2,819 4,804 2,62 5,48 1,825 2,658 3,43 6,04 1,342 1,792 4,16 6,22 1,036 1,305 4,83 6,14 0,819 0,986 5,45 5,87 0,652 0,759 6,04 5,46 0,520 0,587 6,60 4,92 0,410 0,452 7,14 4,28 0,317 0,342 7,66 3,56 0,237 0,251 8,17 2,76 0,167 0,174 8,65 1,90 0,105 0,108 9,13 0,98 0,050 0,051 9,59 0,00 0,000 0,000 facm = 4,1876 Omega(M) = 0,999952 Rho = 0,001082 H0 = 46,654 1/H0 = 21,002 Table 1a

C = 60 r blue v z 0,00 0,00 10,647 25,60 5,14 4,23 2,811 4,799 8,15 5,48 1,822 2,656 10,68 6,04 1,340 1,791 12,93 6,22 1,035 1,304 15,00 6,14 0,818 0,986 16,94 5,87 0,652 0,759 18,78 5,46 0,519 0,587 20,52 4,92 0,410 0,452 22,20 4,28 0,317 0,342 23,81 3,56 0,237 0,251 25,38 2,76 0,167 0,174 26,89 1,90 0,105 0,108 28,37 0,98 0,050 0,051 29,80 0,00 0,000 0,000 facm = 1,3286 Omega(M) = 0,999952 Rho = 0,001082 H0 = 46,646 1/H0 = 21,006 Table 1b

C = 400 r blue v z 0,00 0,00 10,685 25,326 9,68 4,24 2,812 4,793 15,35 5,48 1,823 2,655 20,10 6,04 1,340 1,790 24,34 6,22 1,035 1,304 28,25 6,14 0,818 0,986 31,89 5,87 0,652 0,759 35,34 5,46 0,519 0,587 38,63 4,92 0,410 0,452 41,79 4,28 0,317 0,342 44,83 3,56 0,237 0,251 47,77 2,76 0,167 0,174 50,62 1,90 0,105 0,108 53,39 0,98 0,050 0,051 56,09 0,00 0,000 0,000 facm = 0,6895 Omega(M) = 0,999952 Rho = 0,001082 H0 = 46,637 1/H0 = 21,010 Table 1c

• The parameter r shows the distance of the 100% line or the black line.
• The parameter blue shows the distance of the light ray from the Observer or the blue line.
• The parameter v shows the local expansion speed of the blue line.
• The parameter z shows the value delta l/l or the red shift of the light ray.

The simulations show three important results:

1. The simulations are identical except for the first column i.e. the parameter r.
   For C = 2 the final radius (at t = 14) is 9,59. For C = 2000 the final value is 95,95
   The reason for this behaviour is because C = 8/3 * pi * R^3 * Rho.
   In the case when Lambda is zero then Rho is constant.
   This implies, that when C is increased with a factor of 1000, R increases only with a factor of 10.
2. The parameter z, which we can observe, is independent of C when Lambda is zero.
3. The parameter C is important how far we observe "galaxies" back in time. When C is small we can roughly see 8 billion years ago. When C is large we can Observe the Big Bang (almost).
   This implies in order to observe the Cosmic Micro Wave Background radiation C has to be large.

Answer question 2 - Lambda < 0

The next two pictures (when selected) show the path of a light ray for two different conditions: When Lambda = -0.04 and -0.07

C = 60 Lambda = -0.04 v0 = 3 Figure 6 Overview

c = 60 Lambda = -0.07 v0 = 3 Figure 7 Overview

• The left picture demonstrates the situation When the Universe is almost closed. The blue line starts below the green line and finishes above the green line.
  The reason for this behaviour is because the Universe is contracting the speed of light becomes larger than C.
• The right picture demonstrates the situation when the Universe is closed. The blue line stays completely above the blue line.

Answer question 3 - Lambda > 0

C = 60 Lambda = 0.03 v0 = 3 Figure 8

Figure 9 Detail Figure 9 shows the detail of Figure 8 in the range of 0 to 1 billion years. The black line represents the 100% distance line. The blue line shows the light ray starting from the Big Bang which reaches the Observer now. Figure 8 shows the condition when C=60. In order to study what happens when C=2 select this link: Figure 10: Friedmann C=2

• In order to study the most recent values study this link: Friedmann L=0.01155

When you compare Figure 3 (See Above) with Figure 8 something very important shows up: the two are almost identical. What that means that it is very difficult based on the observed light rays (shape) alone to indicate which one closely represents a specific simulation. Or to say it different which are the correct values of C, Lambda and the parameter "age".

What is necessary is the ralation between z and r.

The following table shows the most important results of the simulations with C= 60 for two different values of Lambda: 0,03 and 0,06.
The First Column shows the time in billion of years, or the distance along the x axis in billion of light years.

t BB 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 - -

Lambda = 0.03 r blue v z 0,00 0,00 3,74 40,020 5,14 3,82 2,56 7,921 8,14 4,87 1,67 4,583 10,65 5,31 1,26 3,210 12,87 5,44 1,01 2,416 14,89 5,36 0,84 1,881 16,76 5,14 0,72 1,485 18,50 4,80 0,61 1,175 20,13 4,37 0,52 0,922 21,67 3,85 0,44 0,710 23,12 3,25 0,36 0,528 24,50 2,57 0,28 0,370 25,80 1,80 0,19 0,232 27,03 0,95 0,10 0,109 28,21 0,00 0,00 0,000 facm = 1,2464 Table 2a

Lambda = 0.06 r blue v z 0,00 0,00 3,56 57,631 5,16 3,52 2,38 11,720 8,31 4,43 1,58 6,902 11,16 4,79 1,20 4,886 13,98 4,88 1,00 3,698 16,93 4,81 0,87 2,880 20.11 4,63 0,77 2,267 23,61 4,35 0,68 1,782 27,54 3,99 0,60 1,386 31,98 3,56 0,53 1,055 37,02 3,04 0,44 0,774 42,79 2,44 0,35 0,535 49,40 1,74 0,25 0,330 56,98 0,93 0,13 0,153 65,70 0,00 0,00 0,000 facm = 1,1865 Table 2b

What Table 2a and Table 2b show, is that Hubble's Law (which claims that there is a lineair relation between z and the distance r) specific for large distances is not true.

t 10 9 8 7 6 5 4 3 2 1 0 0 0,0506 0,0453 0,0400 0,0348 0,0296 0,0245 0,0195 0,0145 0,0096 0,0048 0,0000 0,002 0,0553 0,0495 0,0437 0,0380 0,0324 0,0268 0,0214 0,0159 0,0106 0,0052 0,0000 0,004 0,0598 0,0535 0,0473 0,0412 0,0351 0,0291 0,0231 0,0173 0,0114 0,0057 0,0000 0,006 0,0642 0,0575 0,0508 0,0442 0,0377 0,0312 0,0249 0,0185 0,0123 0,0061 0,0000 Table 2c

Table 2c shows redshift values z for C=60 and k=0 for the Lambda values 0, 0.002, 0.004 and 0,006 in the range from 0 to 1 billion years in increments of 100 million years.

Table 2c shows that for smaller distances Hubble's Law is true.
See also Question 5: Hubble's Law

Table 2d shows the results for C = 60 and different values of Lambda

Lambda rho Omega(M) Omega(L) H0 1/H0 z r max 0 0,001082 0,999952 0 46,646 21,006 0,051 29,80 0,005 0,000852 0,516990 0,483010 57,555 17,024 0,062 32,28 0,01 0,000677 0,298605 0,701395 67,544 14,507 0,073 34,84 0,015 0,000544 0,185588 0,814412 76,769 12,763 0,082 37,48 0,02 0,000440 0,121545 0,878455 85,352 11,480 0,092 40,22 0,03 0,000295 0,058175 0,941825 100,954 9,706 0,109 45,97

Table 2d

The parameter r max is the maximum size of the universe. The values shown in the line t=0 in Table 2a and Table 2b
The parameter z is the value corresponding with the line t=1 in Table 2a and Table 2b. The Lambda value closest to the present value is 0,01.

In order to study the most recent values study this link: Friedmann L=0.01155 Table 2E shows the results for Lambda = 0.01155 and different values of C

C rho Omega(M) Omega(L) H0 1/H0 z r max 60 0,000669 0,266837 0,733163 71,000 13,801 0,076 34,99 100 0,000669 0,266812 0,733188 70,998 13,801 0,076 41,48 150 0,000669 0,266789 0,733211 70,997 13,801 0,076 47,49

Table 2e

What Table 2e shows that the influence of parameter C is very small in relation to the cosmological parameters. The parameter C has a large influence on the size of the Universe.

Answer question 4: Condition Lambda = 0 and k = 1 or k = -1

The following are the results for Lambda = 0, C = 60 and k = 1 (Closed) or k = -1 (Open)

C = 60 Lambda = 0 k = 1 Figure 11

C = 60 Lambda = 0 k = -1 Figure 12

In the above two pictures:

• The "Yellow" line is the function r(t). This function shows the total size of the Universe and is also called the 100% line.
• The "Blue" line is the function a(t). This line shows the size of the Universe when Lambda = 0 and k = 0

• In Figure 11 the "Yellow" line is below the "Blue" line. The reason is because k = 1. The universe is closed. This is similar as when Lambda < 0.
• In Figure 12 the "Yellow" line is above the "Blue" line. The reason is because k = -1. The universe is open. This is similar as when Lambda > 0.

The following tables show more detailed information.

t BB 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 - -

C = 60 k = 1 r blue v z 0,00 0,00 4,139 22,920 5,05 4,40 2,877 4,287 7,93 5,68 1,837 2,369 10,29 6,24 1,334 1,595 12,36 6,41 1,017 1,160 14,24 6,31 0,794 0,875 15,96 6,02 0,626 0,673 17,57 5,57 0,493 0,520 19,08 5,01 0,385 0,400 20,50 4,35 0,294 0,302 21,86 3,60 0,218 0,222 23,15 2,79 0,152 0,154 24,38 1,91 0,095 0,095 25,57 0,98 0,044 0,045 26,70 0,00 0,000 0,000 facm = 1,3797 (Closed) Table 3a

C = 60 k = -1 r blue v z 0,00 0,00 3,856 28,02 5,23 4,10 2,772 5,246 8,37 5,32 1,818 2,900 11,05 5,88 1,350 1,954 13,48 6,08 1,053 1,422 15,74 6,02 0,839 1,074 17,88 5,77 0,674 0,826 19,92 5,37 0,540 0,639 21,89 4,86 0,429 0,491 23,79 4,24 0,334 0,372 25,65 3,53 0,252 0,273 27,45 2,75 0,178 0,189 29,22 1,89 0,113 0,117 30,95 0,97 0,054 0,055 32,65 0,00 0,000 0,000 facm = 1,2855 (Open) Table 3b

L=-0,0025 z 24,519 4,565 2,511 1,683 1,218 0,916 0,700 0,539 0,412 0,310 0,226 0,156 0,096 0,045 0,000 facm = 1,337 Table 3c

L=0,002 z 26,471 4,988 2,774 1,879 1,374 1,043 0,806 0,626 0,484 0,368 0,271 0,189 0,118 0,055 0,000 facm = 1,322 Table 3d

When you compare above:

• The z (redshift) values for table 3a with k = 1 and for table 3c with k = 0 and Lambda = -0,0025 are identical for a distance of roughly 2 billion light years
• The z (redshift) values for table 3b with k = -1 and for table 3d with k = 0 and Lambda = 0,002 are also identical for a distance of roughly 2 billion light years

What that means, if you want to distinguish which of those 2 conditions represents the true state of the Universe, you need at least observations until roughly 4 billion light years.

Answer question 5 - Hubble's Law

The following table is shows the relation between space expansion versus distance in light years for three conditions of C = 60:

Lambda = 0, Lambda < 0 and Lambda > 0

The left column t shows the time since the Big Bang in increments of 1 billion years.
For each condition there are two columns or four columns:

• The column "v" shows the local speed from 14 billion years ago until the present in increments of 1 billion light years.
• The column "z" shows the redshift (delta l/l) from 14 billion years ago until the present in increments of 1 billion light years.
• The column "v1" shows the local speed from 1400 million years ago until the present in increments of 100 million light years.
• The column "z1" shows the redshift (delta l/l) from 1400 million years ago until the present in increments of 100 million light years.

t BB 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 - - -

Lambda = 0 v z v1 z1 3,99 25,60 0,071 0,0728 2,81 4,799 0,066 0,0671 1,82 2,656 0,061 0,0616 1,34 1,791 0,055 0,0561 1,04 1,304 0,050 0,0506 0,82 0,986 0,045 0,0453 0,65 0,759 0,040 0,0400 0,52 0,587 0,034 0,0348 0,41 0,452 0,029 0,0296 0,32 0,342 0,024 0,0245 0,24 0,251 0,019 0,0195 0,17 0,174 0,014 0,0145 0,11 0,108 0,010 0,0096 0,05 0,051 0,005 0,0048 0,00 0,000 0,000 0,0000 q = 0,500 facm = 1,3286 Table 4a

Lambda - 0,04 z z1 10,131 -0,137 1,435 -0,129 0,551 -0,122 0,204 -0,114 0,018 -0,106 -0,095 -0,097 -0,166 -0,088 -0,211 -0,079 -0,236 -0,069 -0,245 -0,059 -0,238 -0,048 -0,215 -0,037 -0,173 -0,025 -0,106 -0,013 0,00 0,000 q = 1,6337 facm = 1,5204 Table 4b

Lambda 0,06 v z v1 z1 3,56 57,631 0,181 0,221 2,38 11,720 0,169 0,203 1,56 6,902 0,157 0,186 1,20 4,886 0,145 0,170 1,00 3,698 0,133 0,153 0,87 2,880 0,120 0,137 0,77 2,267 0,108 0,121 0,68 1,782 0,095 0,105 0,60 1,386 0,082 0,089 0,53 1,055 0,069 0,074 0,44 0,774 0,055 0,059 0,35 0,535 0,042 0,044 0,25 0,330 0,028 0,029 0,13 0,153 0,014 0,014 0,00 0,00 0,000 0,000 q = -0,9843 facm = 1,1865 Table 4c

The above results are very interesting.

• First consider column z1 with Lambda = 0. The z values increase almost linear (going from t=0 to t=14 in increments of 100 million years) that means they are in agreement with Hubbles Law.
• Next consider column z with Lambda = 0. Only the z values going from t=0 to t=5 (in increments of 1 billion years) increase linear. The z values around the Big Bang are not in agreement.
• The same results more or less for Lambda = 0.06.
• Next compare column v and column z for Lambda = 0. For the values for t=5 and earlier they are closely in agreement with the law: v = c * z with c = 1. For the values around the Big Bang this is not.
• Next compare column v and column z for Lambda = 0,06. There is no agreement with the law: v = c * z with c = 1.
• Next consider column v for Lambda = 0. Compare the different results from the bottom up. You get the values: 0,05 0,06 0,06, 0,07 0,08 0,09 0,11 0,13 0,17 0,22 0,30 etc. That means there is acceleration involved along the line of sight.
• Next consider column v for Lambda = 0. Compare the different results from the bottom up. You get the values: 0,13 0,12 0,09 0,07 0,08 0,09 0,10 0,13 0,20 0,36 0,82 1,18 etc. That means at short distance there is deceleration and at larger distance acceleration involved along the line of sight. The reason is the parameter Lambda.

Table 5 shows the Hubble constant H0 (Hubble parameter H at t=0) calculated over a distance of 100 million light year near the observer for different combinations of the parameters Lambda and k. The parameter C = 60.
The parameter 1/H0 is also shown.

Lambda k d v H0 1/H0	q	rho c rho omega(M)
0 0 0,0998 0,0048 0,048 21,00 (1) 0,005 0 0,0998 0,0059 0,059 17,03 0,01 0 0,0997 0,0069 0,069 14,50 0,011 0 0,0996 0,0071 0,0708 14,11 0,0112 0 0,0996 0,0071 0,0712 14,035 0,02 0 0,0996 0,0088 0,087 11,48 0,03 0 0,0995 0,0104 0,103 9,70 0,04 0 0,0994 0,0118 0,117 8,52	0,500 -0,2245 -0,5521 -0,5948 -0,5705 -0,8177 -0,9127 -0,9538	0,00108 0,00108 0,9999 0,00165 0,00085 0,51690 0,00226 0,00067 0,29853 0,00240 0,00065 0,27008 0,00242 0,00064 0,26480 0,00362 0,00044 0,12150 0,00506 0,00029 0,05815 0,00656 0,00020 0,03079
0 1 0,0997 0,0042 0,042 23,91 0,01 1 0,0996 0,0065 0,065 15,361 0,013 1 0,0996 0,0071 0,071 14,034	0,9013 -0,5612 -0,6901	0,000834 0,001503 1,8019 0,00202 0,00091 0,45038 0,00242 0,00079 0,32654
0 -1 0,0997 0,0052 0,052 19,38 0,009 -1 0,0996 0,0070 0,070 14,32 0,0099 -1 0,0996 0,0072 0,072 13,99 0,01 -1 0,0996 0,0072 0,072 13,95	0,3239 -0,4976 -0,5374 -0,5416	0,00127 0,00082 0,64753 0,00232 0,00068 0,27157 0,00244 0,000529 0,21711 0,00245 0,000527 0,21506

Table 5

All the calculations of H and 1/H are based on the assumption that the age of the Universe is 14 billion years.
The Question can be raised if the parameter 1/H is the age of the Universe. In the above examples this is in general not the case.
The only examples are:

• When Lambda = 0,011 and k = 0 the age is 14,11 billion years.
• When Lambda = 0,01 and k = -1 the age is 13,95 billion years.
• When Lambda = 0,013 and k = 1 the age is 14,03 billion years.

(1): The first line of Table 5 shows the Einstein-De Sitter model in which case the age of the Universe is 2/3*1/H i.e. 2/3*21 = 14.

It is also interesting to study the evolution of the redshift or parameter z.

t 0 1 2 3 4 5 6 7 8 9 10 11 12 13 100 mil 110,41 25,59 15,86 11,90 9,66 8,19 7,15 6,35 5,73 5,22 4,80 4,44 4,13 3,86 10 mil 292,62 110,41 73,08 56,64 47,07 40,68 36,08 32,54 29,76 27,49 25,59 23,98 22,60 21,39 Table 6

The left column shows the redshift values in increments of 100 million years for C = 60, Lambda = 0 and k = 0. The value behind t = 13 is calculated for 1.3 billion years after the Big Bang. The value behind t = 0 is calculated for t = 10 million years The right column shows the redshift values in increments of 10 million years. The value behind t = 13 is calculated for 130 million years after the Big Bang. The value behind t = 0 is calculated for t = 1 million years. The results show that the redshift values immediate after the Big Bang can be very large. General relativity is not taken into account.

---

Answer question 6 - 1/H versus the age of the Universe.

The current accepted value for H0 = 71,3 km/sec/Mps. That means 1/H0 = 13,74 billion years. This is defined as the Hubble time. The Hubble time is the value 1/H at t = 0. The Hubble time is not necessary the age of the Universe.

The following table shows the result of a simulation. The maximum age of the Universe is 18. The parameters C, Lambda and k are respectivily: 60, 0.011288 and 0.

The first column shows the age of the Universe. The parameter Rt shows the radius of the Universe.
The parameter H is the Hubble parameter.

when the Age in column 1 is the actual age of the Universe then the Hubble parameter H is the Hubble Constant H0

The parameter 1/H shows the Hubble Time when the Age in column 1 is the actual age of the Universe.

When the age of the Universe is 14 H0 is equal to 0,07142 and the Hubble Time is 14

The parameter Lambda is selected such that at the age of 14 (billion years) the parameter 1/H0 is 14.

Age Rt Q0 H 1/H rho c rho omega(M) 1 5,14718 0,48804 0,66636 1,50068 0,21201 0,21007 0,99087 2 8,18419 0,45055 0,33652 2,97155 0,05407 0,05225 0,96647 3 10,77046 0,39130 0,22758 4,39397 0,02473 0,02292 0,92717 4 13,13049 0,31375 0,17398 5,74771 0,01445 0,01265 0,87558 5 15,36284 0,22231 0,14251 7,01661 0,00969 0,0079 0,81468 6 17,52442 0,12167 0,12211 8,18910 0,00711 0,00532 0,74764 7 19,65347 0,01638 0,10801 9,25828 0,00557 0,00377 0,67747 8 21,77832 -0,08954 0,09783 10,22155 0,00456 0,00277 0,60689 9 23,92156 -0,19275 0,09025 11,08003 0,00388 0,00209 0,53810 10 26,10219 -0,29076 0,08447 11,83774 0,00340 0,00161 0,47277 11 28,33687 -0,38184 0,07999 12,50079 0,00305 0,00125 0,41206 12 30,64071 -0,46497 0,07647 13,07668 0,00279 0,00099 0,35665 13 33,02783 -0,53971 0,07367 13,57362 0,00259 0,00079 0,30683 14 35,51169 -0,60607 0,07142 14,00003 0,00243 0,00063 0,26260 15 38,10535 -0,66436 0,06961 14,36415 0,00231 0,00051 0,22374 16 40,82172 -0,71511 0,06814 14,67381 0,00221 0,00042 0,18991 17 43,67368 -0,75896 0,06695 14,93623 0,00214 0,00034 0,16068 18 46,67425 -0,79662 0,06597 15,15795 0,00207 0,00028 0,13558 Table 6.1

What table 6.1 shows is that the parameter 1/H for each line before t = 14 is larger than the age of the Universe.

For example for t = 13 the calculated value for 1/H is 13.5

What table 6.1 shows is that the parameter 1/H for each line after t = 14 is smaller than the age of the Universe

For example for t = 18 the calculated value of 1/H is 15.2

In order to perform this calculation such that the parameter 1/H is always equal to the age of the Universe, the parameter Lambda has to be modified and becomes a function of t. In that case Lambda is not a Cosmological Constant.

The current accepted position is that the age of the Universe is equal to the Hubble time. See Reflection part 4 - Question 6 for more detail.

The following table is used to test the relation: E(z) = H(z)/H(0) = sqr(rho c(z)/rho c(0))
"rho c" is the critical density

z H(z) E(z) rho c rhoc(z) sqr(rz) omega(M) 1 5,895 0,66636 9,32911 0,21201 87,03234 9,32911 0,99087 2 3,338 0,33652 4,71135 0,05407 22,19686 4,71135 0,96647 3 2,296 0,22758 3,18619 0,02473 10,15181 3,18619 0,92717 4 1,704 0,17398 2,43575 0,01445 5,9329 2,43575 0,87558 5 1,311 0,14251 1,99526 0,00969 3,98109 1,99526 0,81468 6 1,026 0,12211 1,70959 0,00711 2,9227 1,70959 0,74764 7 0,807 0,10801 1,51216 0,00557 2,28663 1,51216 0,67747 8 0,630 0,09783 1,36965 0,00456 1,87596 1,36965 0,60689 9 0,484 0,09025 1,26353 0,00388 1,59652 1,26353 0,5381 10 0,360 0,08447 1,18266 0,0034 1,39868 1,18266 0,47277 11 0,253 0,07999 1,11993 0,00305 1,25424 1,11993 0,41206 12 0,159 0,07647 1,07061 0,00279 1,1462 1,07061 0,35665 13 0,075 0,07367 1,03141 0,00259 1,06381 1,03141 0,30683 14 0,000 0,07142 1 0,00243 1 1 0,2626 Table 6.2

The values for H(0) and rho c(0) are at the bottom line for t = 14 and are respectivily 0,07142 and 0,00243
Table 6.2 shows that the relation is correct for t = 1 to 14.
The reason to demonstrate this relation is Literature (29) Table 1C page 11

---

Answer question 7 - Visible matter, Dark matter and Dark energy

For Visible matter and Dark matter the relation is indirect. For Dark energy the relation is a maybe.
Friedmann's equation describes the relation between objects. In the book "Introducing Einstein's Relativity" by Ray d'Inverno he writes in paragraph 22.3: "it is assumed that the Universe consists of a finite number of Galaxies, each having a mass m(i) etc". The final result is Equation 22.6 which is a function of all the masses m(i) and which consists of three energy terms including one which contains the cosmological constant Lambda. This term is considered to describe dark energy.
This means:

• that Equation 22.6 does not make a distinction between visible and invisible matter
• and that dark energy is a property of all the matter in the Universe.

In fact this raises a serious problem. First you have estimate all Visible matter directly in the Universe including the matter near the outer rim of the Universe i.e. what I call the 100% line. This is difficult because IMO a lot of that mass is very small and difficult to observe.
Next you have to calculate the Total matter in the Universe using Equation 22.6. using different observations (redshift). This is very difficult or maybe impossible because the parameter Lambda is not known.
The difference between the Total matter and the Visible matter is the Dark matter.
What makes this whole exercise even more difficult is that you have to calculate first all the matter (including Dark matter) in all the galaxies (Using galaxy rotation curve) before you can start with all the Dark matter in the space outside the galaxies.

Interesting reading is the following document: Literature (14) Lecture 06: Age of the Universe. In the text near equation 147 is written: Consider a mixture of matter and dark energy rho = rho_m + rho_de etc. IMO such a mixture does not exist because the Cosmological Constant and the Gravitational Constant are qualities of the same objects i.e. galaxies. That means it is very difficult to make a disctinction how much each contributes to actual observations. In that light equation 154, 155 and Figure 7 At page 30 are difficult to understand and to accept.

---

Answer question 8 - Calculation C, Lambda and k based on observations.

The reason why Supernova can be used to calculate distance is because it is assumed that there intrinsic brightness (L) is the same. A supernova is an exploding star. One class is of specific importance and that is the type 1A. They are important because SN of type 1A all explode physical the same i.e. when they explode they all emit the same amount of light (energy).

The most up to date document which shows the relation between magnitude and z based on observations is the document from 2011:

Literature (26) specific Figure 5 at page 32.

See also: Literature (24)
Go to paragraph 5.3.3. and select: Figure 11 (page 14)

What Figure 5 shows is the relation between magnitude and z based on SNLS observations. What we want is the relation between distance and z (or reverse). To calulate the distance based on magtitude you need the Flux/Luminosity relation. The assumption is that the Luminosity (L) is the same for all supernova. The details are discussed below
Using Figure 5 as a mask and using the F/L relation it is possible to calculate the distance based on observations of z. Using the Friedmann equation and based on a certain combination of the parameters parameters C, Lambda and k also a distance is calculated as a function of z. Comparing those two curves it is possible to calculate an error.
With different combinations of the parameters C, Lambda and k it is possible to find the smallest error (the closest fit between the two) and the best values for C, Lamba and k.

It should be emphasized that the object of the SNLS document is to calculate the cosmological parameters omaga(M) and the equation of state parameter w. See Table 7. The object here is to calculate the parameters C, Lambda and k of the Friedmann equation. Using those parameters it is possible to calculate omega(M), omega(Lambda) and omega(k). See Answer: Question 11

In the next 7 paragragh seven different FL relations between magnitude and distance (d) are discussed.

1. F = L/(4*pi*d^2)

   This information can be used to calculate distance.
   The following two sets of calculations are performed:
   1. To go from magnitude (m) to distance (d):
      n = 0 : K = (m-n)/-2.5 : F = 10^K : d = SQR(L/4*pi*F)
      To go from distance (d) to magnitude (m)

      n = 0 : F = L/(4*pi*d*d) : K = 10 Log(F) : m = -2.5*K+n

   Figure 13a z versus magnitude
   -	0,94	3,055	0,00505435	1,78747
   21	1	2,870	0,00505605	1,73305

   Table 7.1

   Figure 13c Detail Lambda between 0 and 0.1

   Nr Lambda L * 10^9 Error 1 0 136,596 0,01034775 5 0,02 92,071 0,00689313 9 0,04 62,591 0,00567553 13 0,06 45,356 0,00531722 17 0,08 34,823 0,0052039 - 0,0824 33,8855 0,00519802 21 0,1 28,016 0,00520296 - 0,1143 24,6194 0,00518310 25 0,12 23,46 0,00519191 29 0,14 20,065 0,0052504 Table 7.1 Detail

   The table shows that there are 3 optimum values for Lambda (smallest error)

   1. One at Lambda = 0.0824
   2. One at Lambda = 0.1143
   3. One at Lambda = 0.94. When you select Figure 13c you will discover that starting from Lambda = 0.7 the error value is almost constant. That means it is very difficult to calculate Lambda accurately.

   IMO the most important issue is the relation between Luminosity (L) and Flux (F).
   

   In Figure 13 the Flux is calculated as: L/4*pi*d^2

   However assume that over larger distances this relation is not correct.

   In Figure 14 the Flux is calculated as: L/4*pi*d^3

   That means the measured Flux values are smaller. The K value will also decrease, but the magnitude m will increase.
   What that means consider Figure 13a and Figure 14a and study the three coloured lines. Those lines are the simulated conditions for different values of Lambda and are a function of x (distance) and z. Take the right hand side and compare the average distance. In figure 4 the lines at the right side are higher as would be expected.
   The black line in both Figure 13a and Figure 14a is identical because that line is a function of m and z.
   In Figure 13b and Figure 14b the reverse situation exists. The coloured lines are fixed and the black line moves. The Flux values on the right hand side are identical. If you call the distance in Figure 13b d and in Figure 14b r than you get the following relation:

   F = L/4*pi*d^2 = L/4*pi*r^3 = Constant

   You can rewrite that as : d^2 = r^3 = Constant.
   That means r (Figure 14b) is smaller than d (Figure 13b). Which is what is observed for the black line.

   F = L/(4*pi*d^2*d)

   F = L/(4*pi*d^2*(1+z))

   Figure 14a z versus magnitude

   Figure 15a z versus magnitude
   	0,91	6,808	0,00164070	1,81668
   21	1	6,200	0,00164190	1,73305

   Table 7.3

   Figure 15c Detail Lambda between 0 and 0.1

   Nr Lambda L * 10^9 Error 1 0 344,384 0,00566396 5 0,02 211,376 0,00295582 9 0,04 137,829 0,00210554 13 0,06 98,1 0,00185863 17 0,08 75,038 0,00181168 19 0,09 66,966 0,00179083 - 0,096903 62,430361 0,00178093 21 0,1 60,531 0,00178222 25 0,12 50,437 0,00184101 Table 7.3 Detail

   The table shows that there are 2 optimum values for Lambda (smallest error)

   1. One at Lambda = 0.096903
   2. One at Lambda = 0.91. When you select Figure 13c you will discover that starting from Lambda = 0.65 the error value is almost constant. That means it is very difficult to calculate Lambda accurately.

   F = L/(4*pi*d^2*(1+d))

   Figure 16a z versus magnitude
   1	0	2093,943	0,00453812	20,89459
   2	0,05	424,277	0,00086602	7,67691
   -	0,097469	176,330	0,000681958
   3	0,1	170,187	0,00068625	5,4729
   -	0,14625	100,7138384	0,000664015
   4	0,15	97,251	0,00066556	4,47235
   5	0,2	65,315	0,00085365	3,87382
   6	0,25	48,700	0,00072810	3,46506
   	0,2841	41,242	0,000620371	3,25015
   7	0,3	38,327	0,00063818	3,16326
   9	0,4	25,981	0,00075753	2,73961
   13	0,6	15,116	0,00098621	2,23706
   17	0,8	10,349	0,00117552	1,93749
   21	1	7,739	0,00133413	1,73305

   Table 7.4

   Figure 16c Detail

   Lambda L * 10^9 Error 0 2093,943 0,00453812 0,02 1034,244 0,00146251 0,04 550,546 0,00092830 0,06 337,615 0,00080924 0,08 230,480 0,00074579 0,097469 176,330 0,000681958 0,1 170,187 0,00068625 0,12 132,000 0,00070700 0,14 106,906 0,00067107 0,14625 100,7138384 0,000664015 0,16 88,931 0,00070427 0,18 75,404 0,00080758 0,2 65,315 0,00085365 Table 7.4 Detail

   The table shows that there are 3 optimum values for Lambda (smallest error)

   1. One at Lamba = 0.097469
   2. One at Lamba = 0.14625
   3. One at Lamba = 0.2841 This one shows the smallest error value.

   F = L/(4*pi*d^2*(1+z)^2)

   Figure 17a z versus magnitude
   1	0	743,242	0,0021986	20,89459
   -	0,019654	435,7513	0,00014195
   2	0,05	227,557	0,0008190	7,67691
   3	0,1	118,45	0,00090210	5,47290
   4	0,15	79,226	0,00084130	4,47235
   	0,16875	70.595	0,00078566	4,21694
   5	0,2	60,095	0,00085676	3,87382
   9	0,4	30,390	0,00104048	2,73961
   13	0,6	20,259	0,00104978	2,23706
   17	0,8	15,202	0,00105885	1,93749
   21	1	12,163	0,00106720	1,73305

   Table 7.5

   Figure 17c Detail

   Lambda L * 10^9 Error 0 743,242 0,0021986 0,01 563,414 0,0008097 0,019654 435,751 0,000141954 0,02 431,906 0,00014315 0,03 339,227 0,00047669 0,04 274,285 0,00071430 0,05 227,557 0,00081900 0,06 193,353 0,00089824 0,07 167,358 0,00090472 0,08 147,595 0,00093738 0,09 131,506 0,00093987 0,1 118,450 0,00090210 Table 7.5 Detail

   The table shows that there are 2 optimum values for Lambda (smallest error)

   1. One at Lamba = 0.019654 This one shows the smallest error value.
   2. One at Lamba = 0.16875

   F = L/(4*pi*d^2*(1+alpha*d)^2)

   The following table shows the parameter alpha as a function of error.
   In order to calculate alpha both Lambda Fitting and Luminosity Fitting are used. The purpose of this exercise is to calculate alpha which gives the smallest error between theory and observation. The result is alpha = 0,145.

   Figure 18a

   alpha Lambda L * 10^9 Error 0,13 0,0455 222,097 0,0002713 0,14 0,0609 164,444 0,0002223 0,145 0,06344 161,09917 0,00020676 0,15 0,0656 158,749 0,0002161 0,16 0,0833 121,156 0,0002481 0,17 0,0921 111,212 0,0002272 0,18 0,0979 107,317 0,0002538 Table 7.6.1

   The following table shows Lambda as a function of error.
   In order to calculate Lambda Luminosity Fitting is used.
   

   The parameter Alpha = 0.145

   Figure 18b

   Nr Lambda L * 10^9 Error 1/H 1 0 1260,645 0,0032479 20,89459 - 0,0634 161,0986 0,00020676 3 0,1 86,921 0,00057687 5,47290 5 0,2 33,901 0,00152054 3,87382 7 0,3 20,357 0,00170848 3,16326 9 0,4 14,087 0,00201326 2,73961 11 0,5 10,634 0,00223821 2,45048 13 0,6 8,485 0,00241394 2,23706 15 0,7 7,020 0,00255671 2,07119 17 0,8 5,971 0,00267751 1,93749 19 0,9 5,181 0,00278079 1,82674 21 1,00 4,566 0,00287027 1,73305 Table 7.6.2

   Figure 18b Detail

   Nr Lambda L * 10^9 Error 1 0 1260,645 0,0032479 5 0,02 564,269 0,00071551 9 0,04 287,664 0,00038335 13 0,06 173,391 0,00022008 - 0,0634 161,0986 0,00020676 15 0,07 141,091 0,00025897 17 0,08 117,739 0,00036151 21 0,1 86,921 0,00057687 Table 7.6.2 Detail

   The table shows that the optimum value for Lambda = 0.0634

   F = L/(4*pi*d^2*(1+alpha*d+beta*d^2)

   In order to calculate alpha and beta both Lambda Fitting and Luminosity Fitting are used. The purpose of this exercise is to calculate the parameters alpha and beta which give the smallest error between theory and observation. There are two solutions:

   1. The first result is alpha = 0,163 and beta = 0.2197
   2. The second result is alpha = 0,204 and beta = 0.766

   The following table shows the parameter alpha as a function of error.
   The parameter Alpha = 0.163 The parameter Beta = 0.2197

   Figure 19a

   alpha Lambda L * 10^9 Error 0,140 0,0423 205,36 0,0001699 0,150 0,0429 206,084 0,0001637 0,160 0,044 204,357 0,0001625 0,163 0,0445 202,583 0,0001622 0,170 0,0447 204,54 0,0001634 0,180 0,0449 207,814 0,0001691 Table 7.7.1

   The following table shows beta as a function of error.
   In order to calculate Lambda Luminosity Fitting is used.
   The parameter Alpha = 0.204 The parameter Beta = 0.766

   Figure 19c

   Nr Beta Lambda L * 10^9 Error 1 0,016 0,0429 211,151 0,0003592 9 0,024 0,0596 155,550 0,0001775 10 0,025 0,0617 149,959 0,0001782 20 0,035 0,0890 99,704 0,0002342 30 0,045 0,1051 84,542 0,0002607 40 0,055 0,1352 62,770 0,0002823 50 0,065 0,1558 53,769 0,0001921 60 0,075 0,1660 51,417 0,0001139 0,0766 0,1680 50,863 0,0001127 70 0,085 0,1790 48,137 0,0001564 80 0,095 0,1987 43,152 0,0002394 Table 7.7.3

   The following table shows Lambda as a function of error.
   In order to calculate Lambda Luminosity Fitting is used.
   The parameter Alpha = 0.204 The parameter Beta = 0.766

   Figure 19e

   Nr Lambda L * 10^9 Error 1/H 1 0 2440,011 0,00169228 20,89459 0,005 1920,304 0,00132201 3 0,1 110,766 0,00101839 5,4729 0,16815 50,84027 0,0001127 4.22446 0,17 50,037 0,00011621 5 0,2 39,632 0,00035848 3,87382 7 0,3 22,652 0,00079111 3,16326 9 0,4 15,248 0,00124387 2,73961 13 0,6 8,892 0,00184551 2,23706 17 0,8 6,139 0,00223959 1,93749 21 1 4,639 0,00252427 1,73305 Table 7.7.5

   Figure 19e Detail

   Nr Lambda L * 10^9 Error 1 0 2440,011 0,00169228 2 0,005 1920,304 0,00132201 3 0,01 1498,567 0,00154418 21 0,10 110,729 0,00101838 33 0,16 54,693 0,00017016 0,16815 50,84027 0,0001127 35 0,17 50,037 0,00011621 37 0,18 46,054 0,00019386 Table 7.7.5 Detail

   The table shows that there are 2 optimum values for Lambda (smallest error)

   1. One at Lamba = 0.005
   2. One at Lamba = 0.16815 This one shows the smallest error value for F/L relation #7 and also the smallest error value among all seven tested F/L relations.

• Summary: Flux Luminosity Relation - Age 14

  The results of the seven FL relations are summarised in the following table:

  Nr Description Lambda L * 10^9 1/H Error Omega(M) 1.1 F = L/(4*pi*d^2) 0.11432 24,619 5.12044 0.0051831 0,00109 1.2 F = L/(4*pi*d^2) 0.94 3,055 1.78747 0.00505435 0 2 F = L/(4*pi*d^2*d) 0.01937 944,219 11.60739 0.0018039 0,12786 3.1 F = L/(4*pi*d^2*(1+z)) 0.09690 62,432 5.55897 0.0017809 0,00210 3.2 F = L/(4*pi*d^2*(1+z)) 0.91 6,887 1.82674 0.0016418 0 4.1 F = L/(4*pi*d^2*(1+d)) 0.14625 100,713 4.52922 0.0006640 0,00037 4.2 0,2841 41,242 3,25015 0,000620371 0,00001 5.1 F = L/(4*pi*d^2*(1+z)^2) 0.01965 435,752 11.54382 0.0001419 0,12498 5.2 0.012 533,602 13.739 0.000607 0,24502 6.1 F = L/(4*pi*d^2*(1+alpha*d)^2) 0,06344 161,098 6.84648 0.0002067 0,00885 6.2 F = L/(4*pi*d^2*(1+alpha*d)^2) 0,012 1068,957 13.739 0.001058 0,24502 7.1 F = L/(4*pi*d^2*(1+alpha*d+beta*d^2) 0,04457 202,583 8.10498 0.0001622 0,02361 7.2 0,16815 50,84027 4.22446 0.0001127 0,00019 7.3 0,012 435,454 13.739 0.000418 0,24502

  Table 8 FL relation 1 shows two minimum conditions.
  FL relation 3 shows two minimum conditions.
  FL relation 4 ex1 and ex 2 both show minimum conditions.
  In FL relation 6 ex 1 the value of alpha = 0.145
  In FL relation 6 ex 2 the value of alpha = 0.1886
  In FL relation 7 ex 1 the value of alpha = 0.163 beta = 0.02197
  In FL relation 7 ex 2 the value of alpha = 0.204 beta = 0.0766
  In FL relation 7 ex 3 the value of alpha = -0,0579 beta = 0.0287
  

  FL relation 7 shows the smallest error between observations and theory (Friedmann equation)

  Of specific importance are FL relation Ex 2, FL relation 6 ex 2 and FL relation 7 Ex3. Each of those show the same 1/H value of 13,739 billion years. This is equivalent with the Hubble parameter value of 71,316 km/sec/Mpc. The importance becomes obvious if you compare this with the same values of Table 13 for an universe of 28 billion years.

  Lambda versus error for F/L 1 to 7 Figure 20 A

  Figure 20 A shows Lambda values for six F/L relations for Lambda between 0 and 1.
  
  • F/L relation #1 and #3 are similar in the sense that in both cases it is very difficult to calculate Lambda. Starting from Lambda = 0.7 the error value is almost constant.
    
  • F/L relation #7 shows the smallest error between theory and observation

• Summary: curvature constant k values

  Using Labda Fitting and Luminosity Fitting it also possible to calculate error values using different values of k.
  Only the values k = -1, k = 0 and k = 1 are possible. See: Literature (13) "Lecture 5: Solutions of Friedmann Equations"
  The book "Introducing Einstein's Relativity" by d'Inverno in chapter 23 "Cosmological Models" does the same.
  The document The Friedmann Equation considers the three cases: k=0, k<0 and k>0 (Select: curvature Parameter)

  Figure 19 shows the error values for k between -2 and 2 for three FL relations.

  1. The red line is FL relation 5 (method 4)
  2. The green line is FL relation 6 (method 5) alpha = 0,145
  3. The blue line is FL relation 7 (method 6) alpha = 0,163 beta=0,02197

  k between 2 and -2 Figure 20 B

  1. FL relation 5 - method 4

     nr k Lambda L * 10^9 Error 1 2 0,0211 491,241 0,0001608 11 1 0,0199 462,574 0,0001345 12 0,9 0,0199 462,574 0,00013427 21 0 0,0196 435,734 0,0001419 31 -1 0,0196 414,48 0,0001455 41 -2 0,0194 401,157 0,0001481 Table 9.4

  2. FL Relation 6 - method 5

     nr k Lambda L * 10^9 Error 1 2 0,0688 151,65 0,0002051 8 1,3 0,06724 153,655 0,00020162 11 1 0,0666 154,445 0,0002022 21 0 0,0634 161,1 0,0002067 31 -1 0,0621 162,135 0,0002176 41 -2 0,0595 168,361 0,0002316 Table 9.5

  3. FL Relation 7 - method 6

     nr k Lambda L * 10^9 Error 1 2 0,0555 165,475 0,0001972 11 1 0,0482 191,132 0,0001778 21 0 0,0445 202,59 0,0001622 31 -1 0,0416 211,475 0,0001753 41 -2 0,0403 212,176 0,0002085 Table 9.6

  4. FL relation 2-7

     The following table shows the curvature constant k values for 6 FL relations with the smallest error value between theory and observation.
     

     • Column 1 shows the Flux Luminosity relation.
     • Column 2 shows the Table Nr which gives more detail.
     • Column 3 shows the measurement point in the corresponding figure.
     • Column 4 shows the curvature constant k value with the smallest error value

     FL Table nr k Lambda L * 10^9 Error 2 9.1 18 -11 0,0193 664,766 0,0017059 3 9.2 1 7 0,0663 181,602 0,0004725 4 9.3 1 8 0,158 96,626 0,0006094 5 9.4 12 0,9 0,0199 462,574 0,00013427 6 9.5 8 1,3 0,06724 153,655 0,00020162 7 9.6.1 21 0 0,0445 202,59 0,0001622 7 9.6.2 37 -14 0,1649 51,738 0,00011231 Table 9.7

• Summary: age calculation

  Figure 21 A shows the error value as a function of age, with age going from 14 to 28 billion years. The error value is the difference between theory and observation. This calculation requires both the Friedmann equation and the Flow Luminosity relation.
  In Figure 21 A this is relation # 4.
  In Figure 21 B FL relation #5 is used
  In Figure 21 C FL relation #6 is used
  In Figure 21 D FL relation #7 is used
  

  Figure 21 A F/L relation 4	Figure 21 B F/L relation 5
  Figure 21 C F/L relation 6	Figure 21 D F/L relation 7

• Summary: C calculation

  C between 5 and 100 Figure 22 A

  K = 0 Nr C Lambda L * 10^9 Error 1 5 0,0196 435,674 0,000142 4 20 0,0196 435,719 0,0001419 8 40 0,0196 435,740 0,0001419 12 60 0,0196 435,749 0,0001419 16 80 0,0196 435,755 0,0001419 20 100 0,0196 435,772 0,0001419

  C between 5 and 100 Figure 22 B

  Nr C Lambda L * 10^9 Error 1 5 0,1681 50,842 0,00011275350 4 20 0,1681 50,842 0,00011275361 8 40 0,1681 50,843 0,00011275369 12 60 0,1681 50,841 0,00011275370 16 80 0,1681 50,840 0,00011275373 20 100 0,1681 50,841 0,00011275377

  What Figure 22 A clearly shows is that for FL relation 5 (method 4) with k =0 (the blue line) the parameter C is independent of the error value (Difference between theory and observation). That means it is not possible calculating the parameter C.
  Figure 22 B For FL relation 7 (method 6) shows the same behaviour.

Answer question 9 - Age = 28 and Age = 42

• Figure 23a (23b) shows the same information as Figure 14a (14b) except over a period of 28 billion years

  Figure 23a z versus magnitude

  Figure 23b z versus distance

  4. F = L/(4*pi*d^2*(1+d))

  Lambda L * 10^9 Error 0 16338.4 0.010149 0.01 4161.731 0.001992 0.011 3721.976 0.001962 0.011022 3716.043 0.001962 0.012 3356.378 0.001992 0.013 3038.983 0.002010 0.02 1708.5 0.002164 0.03 959.7 0.002225 0.05 461.7 0.00225 0.1 169.1 0.00228

  Table 10.1

  5. F = L/(4*pi*d^2*(1+z)^2)

  Lambda L * 10^9 Error 0 2942.5 0.003961 0.005 1750.7 0.000598 0.005624 1623.848 0.000419 0.006 1571.4 0.000439 0.007 1423.8 0.000666 0.008 1314.8 0.000909 0.01 1106.763 0.001258 0.02 602.3 0.002145 0.03 402.3 0.002650 0.05 237.2 0.002763 0.1 116.4 0.003361

  Table 10.2

• Figure 24a (24b) show the same information as Figure 14a (14b) except over a period of 42 billion years

  Figure 24a z versus magnitude

  Figure 24b z versus distance

  4. F = L/(4*pi*d^2*(1+d))

  Lambda L * 10^9 Error 0 52912,178 0.006829 0.003 20483,102 0.001936 0.004257 14436,282 0.001734 0.01 4763,150 0.002085 0.02 1747,485 0.002211 0.03 966,907 0.002272 0.04 635.669 0.002244 0.05 460.181 0.002252 0.1 168,463 0.002275

  Table 10.3

  5. F = L/(4*pi*d^2*(1+z)^2)

  Lambda L * 10^9 Error 0 6732,037 0.003278 0.002466 3688,605 0.000315 0.003 3291,119 0.000449 0.01 1208,331 0.001811 0.02 606,647 0.002177 0.03 400,415 0.002718 0.04 303,918 0.002850 0.05 237,432 0.003240 0.1 117.352 0.004041

  Table 10.4

What Figure 14, 23 and 24 (a and b) demonstrate is that it is not possible to calculate the age of the universe based on the information supplied in the "3 years SNLS document"

The following table shows the redshift values or z values immediate after the Big Bang in billions of years for different combinations of the parameter Lambda. The age of the Universe is respectively: 14 or 28 or 42 billion years.
The left column shows the age of the Universe after the Big Bang in billion of light years.
Age 0 is not the moment of the Big Bang but 100 million years after the Big Bang.

t BB 0 1 2 3 4 5 6 7 8 9 10 1/H q0 - -

L=0 0.01 0.02 0.03 z z z z 25,120 29,53 34,249 39,29 4,781 5,75 6,79 7,89 2,651 3,25 3,89 4,575 1,788 2,23 2,71 3,206 1.303 1,65 2,02 2,414 0,985 1,27 1,57 1,879 0,758 0,99 1,24 1,484 0,587 0,78 0,97 1,174 0,452 0,61 0,76 0,921 0,342 0,46 0,59 0,710 0,251 0,35 0,44 0,528 21 14,51 11,481 9,70 0,5 -0,552 -0,817 -0,913 age = 14 Table 11a

L=0 0.01 0.02 0.03 z z z z 40,457 71,49 111,92 163,9 8,175 15,03 23,95 35,4 4,794 9,10 14,67 21,8 3,426 6,68 10,87 16,2 2,655 5,30 8,69 12,98 2,151 4,39 7,23 10,8 1,790 3,73 6,16 9,17 1,518 3,23 5,33 7,9 1,304 2,82 4,65 6,8 1,130 2,48 4,09 6,0 0,986 2,20 3,61 5,2 42,01 17,054 12,224 9,998 0,500 -0,954 -0,994 -0,998 age=28 Table 11b

L=0 0.01 0.02 0.03 z z z z 53,322 162,45 353,77 1163 11,023 35,14 77,30 255 6,593 21,77 48,20 159 4,799 16,32 36,27 119 3,789 13,22 29,42 96 3,128 11,16 24,84 80 2,656 9,68 21,49 68 2,300 8,53 18,87 59 2,019 7,61 16,75 51 1,791 6,86 14,98 45 1,602 6,21 13,47 40 63 17,299 12,25 8,662 0,5 -0,996 -0,999 -1,000 age=42 Table 11c

In the following document Literature (30) the chemical contents of two galaxies is discussed which are less then 2 billion years old.
In that document at page 9 the relation age versus redshift or z is discussed. At present z = 0 and near the Big Bang z = 7. Roughly 2 billion years z is approximate 3.5 which coincide with the age of the two galaxies or slightly earlier. The question is if that argumentation is correct.

Table 11a first column shows the evolution of z for Lambda=0 over a period of 14 billion years. At 1,4 billion years after the Big Bang z=3.630. At 1.5 billion years z=3.423. The measured value of z=3.57 is somewhere in between.

The question is does Table 11a show the right condition of the Universe. When you consider that the age of the Universe is 28 billion years old than the value of z=5.7 is between 2.8 and 2.9 billion years after the big bang. When the age of the Universe is 42 billion years between z=3.565 after 4.3 billion years. What that means that there is a clear linear relation between the age of the Universe and the age of an event for the same redshift value.

The 4 columns of Table 11a shows Lambda values of: 0 0.01 0.02 and 0.03 Table 11a and Table 11b show that for the same event (same z value) when you increase the age of the universe with a factor 2 that than also the age of the event increases. When Lambda is considered non zero the age of the event increases more. For example with L=0.03 and z=3.57 and age=14 the event happened at approximate 2.75 billion years
With L=0.01 and age=28 the event happened at approximate 6.5 billion years, with L=0.02 at approximate 11 billion years and with L=0.03 at approx 13 billion years

• When Lambda=0 and k=1 for an assumed age of 14 billion years z=3,536 after 1.6 billion years.
• When Lambda=0 and k=-1 for an assumed age of 14 billion years z=3,687 and 3.450 after 1.2 and 1.3 billion years.

Summary: Flux Luminosity Relation - Age 28

The results of the seven FL relations assuming an age of the universe of 28 billion years are summarised in the following table:

Nr Description Lambda L * 10^9 Error 1/H rho c rho Omega M 1 F = L/(4*pi*d^2) 0.03744 76,055 0.0050636 8,950 0,00149 0 0,00034 2 F = L/(4*pi*d^2*d) 0.00548 6936,51 0.0018405 22,142 0,000243 0,000025 0,1045 3 F = L/(4*pi*d^2*(1+z)) 0.09440 64,530 0.0017468 5,6383 0,00375 0 0 4 F = L/(4*pi*d^2*(1+d)) 0.09862 175,310 0.0006804 5,5164 0,00392 0 0 5.1 F = L/(4*pi*d^2*(1+z)^2) 0.004904 1760,50 0.0001404 23,132 0,000223 0,000028 0,1254 5.2 0.0158 744,998 0.000941 13,718 0,00063 0,0000056 0,00896 6.1 F = L/(4*pi*d^2*(1+alpha*d)^2) 0,06445 156,098 0.0001932 6,8235 0,00256 0 0,00002 6.2 0.012865 759,067 0.000291 15.1472 0,00052 0,0001 0,01619 6.3 0.0158 642,811 0.000195 13,718 0,00063 0,0000056 0,00896 7.1 F = L/(4*pi*d^2*(1+alpha*d+beta*d^2) 0,03840 254,583 0.0001433 8,83852 0,00153 0 0,00030 7.2 0,0158 564,313 0.000131 13,718 0,00063 0,0000056 0,00896

Table 12 In FL relation 6.1 the value of alpha = 0.14
In FL relation 6.2 the value of alpha = 0.70193
In FL relation 6.3 the value of alpha = 0.0711
In FL relation 7.1 the value of alpha = 0.195 beta = 0.0114
In FL relation 7.2 the value of alpha = 0.09046 beta = 0.00629

Of specific importance are FL relation 5 Ex 2, FL relation 6 ex 3 and FL relation 7 Ex 2. Each of those show the same 1/H value of 13,718 billion years. This is equivalent with the Hubble parameter value of 71,318 km/sec/Mpc. The importance becomes obvious if you compare this with the same error values of Table 8 for an universe of 14 billion years. The errors in Table 12 are smaller. This means the Universe is older than 14 billion years.

The following table shows FL relations for an Universe of 21 billion years.

Nr Description Lambda L * 10^9 Error 1/H rho c rho Omega M 5.1 F = L/(4*pi*d^2*(1+z)^2) 0.0151 703,586 0.000598 13,777 0,00063 0,000028 0,0474 6.1 F = L/(4*pi*d^2*(1+alpha*d)^2) 0.0151 717,027 0.000396 13,777 0,00063 0,000028 0,0474 7.1 F = L/(4*pi*d^2*(1+alpha*d+beta*d^2) 0.0151 551,323 0.000169 13,777 0,00063 0,000028 0,0474

Table 12.1 In FL relation 6.1 the value of alpha = 0.0885
In FL relation 7.1 the value of alpha = 0.0680 beta = 0.0099

---

Answer question 10: The parameter q

Accordingly to feedback received the best document to study to calculate the parameters of the Friedmann equations is: Literature (1) Authors: S. Refsdal; R. Stabell; and F.G. de Lange in 1967
In that document the parameter q is used, called deceleration parameter.

q is defined as: -R*a(R)/v(R) with V(R)=dR/dt and a(R) as dv(R)/dt

See Table 4 the right column, for q values from different combinations of Lambda and k

The reason why the parameter q is used in the document to calculate the parameters of the Friedmann equation is not clear because the parameter q can not be directly observed. The calculation of q requires the three values R, v(R) and a(R) and those values are easy to calculate using the Friedmann equation. But R is a global parameter and impossible to observe.
To calculate q based on observations you need:

1. The distance of a galaxy.
2. The speed of a galaxy
3. The acceleration of a galaxy

The first two are relative simple because you can use the redshift (z) parameter.
The third one is very difficult because you must follow the galaxy over a long period of time and measure the change in z value.

Answer question 11: The parameters omega(M), omega(Lambda) and omega(K)

The equations and pages mentioned in this paragraph are from the book: "Introducing Einstein's Relativity" by Ray d'Inverno.
The next steps define omega(Matter), omega(Lambda) = omega dark energy and omega(K).

1. starting point is the equation 23.1 used above:
   (dR/dt)^2= C/R + 1/3 * Lambda*R^2 - k
   using equation 22.57 C= (8*pi/3)*R^3*rho we get:

   (dR/dt)^2= (8*pi/3)*R^2*rho + 1/3 * Lambda*R^2 - k

   dividing all components by R^2 and substituting H=(dR/dt)/R we get:

   H^2= (8*pi/3)*rho + Lambda/3 - k/R^2

   rhoc (rho crital) is defined in equation (23.36) as: (3/8*pi)*H0^2
   

   substituting 8*pi/3 with H0^2/rhoc we get:

   H^2= H0^2*(rho/rhoc) + Lambda/3 - k/R^2

   and next:

   H^2= H0^2 * (rho/rhoc + Lambda/(3*H0^2) - k/(R^2*H0^2))

   With is equal to:

   H^2=H0^2 * (omega(M) + omega(Lambda) +omaga(K))

   omega(Matter) is defined at page 355 as: rho/rhoc

   with H2 = H0 at t = 0 this leads to:

   omega(M) + omega(Lambda) +omaga(K) = 1

The following table shows the results.

Nr Lambda C k L Error 1/H omega(M) rho c rho omega(L) omega(k) 1 0 60 0 742,601 0.0021988 21,00127 0,99995 0.0002705 0.0002705 0 0 2 0 60 -1 688,218 0,0018941 19,38226 0,64757 0,0003177 0,0002057 0 0,35239 3 0 60 +1 827,009 0,0026405 23,91846 1,80202 0,0002086 0,0003760 0 -0,80211 4 0 10 0 743,174 0,0021985 21,00485 0,99995 0,0002705 0,0002705 0 0 5 0 10 -1 612,028 0,0015821 17,45902 0,32068 0,0003915 0,0001255 0 0,6793 6 0 10 +1 1213,289 0,0061800 115,93216 137,37738 0,0000088 0,0122101 0 -136,37858 7 0.01 60 0 563,414 0,0008097 14,50704 0,29856 0,0005672 0,0001693 0,70144 0 8 0.01 60 -1 528,691 0,0007038 13,95589 0,21508 0,0006128 0,0001318 0,64916 0,13576 9 0.01 60 +1 615,291 0,0009574 15,36127 0,45043 0,0005058 0,0002278 0,78646 -0,23689 10 0.01 10 0 563,320 0,0008099 14,50637 0,29862 0,0005672 0,0001693 0,70144 0 11 0.01 10 -1 480,246 0,0005968 13,21788 0,12178 0,0006832 0,000083 0,58237 0,29591 12 0.01 10 +1 881,684 0,0024968 21,98605 2,51915 0,0002469 0,0006220 1,61128 -3,13042 13 0.01211 60 0 531,996 0,0005964 13,70001 0,24244 0,0006359 0,0001541 0,75764 0 14 0.01211 10 0 531,984 0,0005966 13,69951 0,24250 0,0006360 0,0001542 0,75758 0 15 0.01211 2 0 531,878 0,0005967 13,69922 0,24253 0,0006360 0,0001542 0,75755 0 16 0.010724 60 -1 518,883 0,0006356 13,70016 0,20096 0,0006359 0,0001278 0,67094 0,12817 17 0.008468 10 -1 497,871 0,0007123 13,70019 0,13910 0,0006360 0,0000884 0,52980 0,33111 18 0.005389 2 -1 468,779 0,0008690 13,70014 0,06713 0,0006360 0,0000426 0,33716 0,59575

Table 13 - method = 4

• In line #1 with k=0 the parameter 1/H = 21 and Omega(M) = 1, Omega(Lambda)= 0. As expected.
  In line #4 with k=0 the parameters 1/H and omega are the same as in line #1. Also as expected.
  In both lines the parameter rho shows rhoc (Rho critical)
• In line #2 with k=-1 Omega(M) = 0.76, Omega(Lambda)= 0. This means that Omega(k) = 0.24
  
• In the lines #7 to #9 the parameter Lambda = 0.02. The error value is much lower compared with the lines #1 to #3 with Lambda = 0.
  That means Lambda = 0.02 seems to be a better fit.
• In the lines #13 to #15 the parameter Lambda = 0.02. The error value is much lower compared with the lines #10 to #12 with Lambda = 0.
• The difference between the lines #7 to #9 and #13 to 15 is the method used. In the first combination this is F/L #5 and in the second combination this is F/L #1.

The most important consideration of the above table is that the calculated values: 1/H, omega and rho are independent of the F/L relation selected.

The values most often mentioned in the Literature are Omega(M) = 0.28, Omega(Lamba)=0.72, Omega(K)=0
For example See:

• Literature (15) page 758 and page 771 Figure 15.
  The object of this "AJ iopscience" document is to calculate the parameters omega(Lambda), omega(M) and the equation of state parameter w. The basic assumption is that the universe is flat i.e. that k = 0
  The same document is also: Literature (16) page 11 and page 23 Figure 15. This "arxiv.org" version of the document contains the "raw" data values.
• Also see for example Literature (8). This is a document from 1999 and shows the values omega(M)=0.28 and omega(Lamba)=0.72
• See Literature (31) This "arxiv.org" document gives for omega(M) (See Table 1 and Figure 1) a value of 0.7. That means omage(L) = 0.3. Observing Table 8 this is the value close for F/L relation 2 and 5. The same document also mentions omega(M) of 1. That means omega(L) = 0. That is the value close to the other F/L relations.

What this means that it is difficult to calculate the parameters of the Friedmann equation and other cosmological parameters.

The following table shows the parameters omega(M) and omega(Lambda) as a function of Lambda for C = 60 and k=0.

Lambda L Error 1/H omega(M) omega(L) 0 743,242 0,0021986 21,00709 0,99995 0 0,002 703,181 0,0018497 19,16382 0,75515 0,24484 0,004 665,971 0,0015294 17,67046 0,58368 0,41631 0,006 630,534 0,0012515 16,43500 0,45981 0,54018 0,008 595,884 0,0010242 15,39509 0,36803 0,63196 0,01 563,414 0,0008097 14,50704 0,29856 0,70143 0,011 548,238 0,0007064 14,10974 0,27010 0,72989 0,012 533,601 0,0006070 13,73928 0,24502 0,75497 0,013 519,457 0,0005125 13,39297 0,22282 0,77717 0,014 505,833 0,0004239 13,06845 0,20311 0,79688 0,015 492,691 0,0003425 12,76370 0,18555 0,81444 0,016 479,892 0,0002704 12,47690 0,16986 0,83013 0,018 455,014 0,0001731 11,95101 0,14317 0,85682 0,019 443,200 0,0001477 11,70927 0,13179 0,86820 0,02 431,906 0,0001431 11,48014 0,12151 0,87848 0,022 410,708 0,0001904 11,05585 0,10378 0,89621 0,024 391,052 0,0002711 10,67132 0,08914 0,91085

Table 14 What the table shows is that for Lambda = 0.011 omega(M) = 0.27 omega(Lambda) = 0.73. This is the current most accepted value for omega(Lamba).
It is important to remark that this particular value has nothing to do with the F/L relation selection. In the above table this is #5 (method = 4).
The above table shows that the smallest error value is for Lambda = 0.02 with method = 4 (F/L relation = 5)

1. An important document to study is: Literature (28) Submitted on 17 May 2011.
   Specific study the text at the bottom of page 19:
   

   To examine constraints on the existence of dark energy at different epochs, we study rho(z), which is the density of the dark energy and allowed to have different values in fixed redshift bins. Within each bin, rho is constant. (Note that the discontinuities in rho(z) at the bin boundaries introduce discontinuities in H(z).) We choose the same binning as above, but note that binned rho and binned w models give different expansion histories. Our results are shown in Figure 9 and Table 8

   Table 8 at page 22 shows the parameter rho(DE)/rho(0) for 4 bins:

   z <0.5 0.5 < z < 1.0 1.0 < z<1.6 z > 1.6 0.731 0.85 0.23(0.33) 0.9(0.7)

   The parameter rho(DE)/rho(0) is the same as omega(Lambda)
   Specific the third value is interesting because this means that also much smaller values for omega(Lambda) are possible.
   It should be remarked that in this study all the cosmological parameters are calculated based on the total curve ( z between 0.5 and 1.4) and not based on bins.

   Also important is the following document:Literature (22)
   This document is important to study the best fitted cosmological parameters: Z, Omega(m), Omega(w) and w.
   See paragraph 7.2 "Fitting Cosmology" (page 724):

   The blind technique is implemented by adjusting the magnitudes of the SNe until they match a fiducial cosmology (Omega(M) = 0.25, w = -1). This procedure leaves the residuals only slightly changed, so that the performance of the analysis framework can be studied. This seems to me that this document is biased towards the values of Omega(L) = 0.75 and Omega(M) = 0.25

   Also important is the following document: Literature (25)
   In paragraph 3.2.4 Luminosity Distances at page 13 we read:

   There is an indication that the constraints on dark energy parameters are different when different methods are used to fit the light curves of Type Ia super-novae

   and:

   For example, Omega(Lambda) derived from WMAP+BAO+SALT-II and WMAP+BAO+MLCS2K2 are different by nearly 2 sigma, despite being derived from the same data sets (but processed with two different light curve fitters).

   This is inline with the different Flux/Luminosty functions discussed above

The following table shows omaga(M) and omega(L) for different age's of the Universe. The 1/H values are such that they are close to the age of the Universe.

age Lambda 1/H H in Mpc omega(M) omega(L) 14 0,01129 13,999 69,878 0,26255 0,73745 16 0,00864 16,001 61,136 0,26267 0,73733 20 0,00553 20,000 48,911 0,26270 0,73730

Table 14 a What the above table shows it that also all the omega(M) values are identical
This raises the serious observation to what extend SNLS data is used to establish the parameters of the Friedmann equation.

Question 12: Cosmic Cincidence problem

The Cosmic Coincidence problem claims that the parameter 1/H0 and the Age of the Universe are almost identical. The Following table explains this:

Age Lambda Omega(M) 1/H0 H0 Omega(m)*h^2 10 0,022124 0,26259 10,00047 97,818 0,25122 14 0,011289 0,26257 13,99965 69,878 0,12820 18 0,006828 0,26258 17,99989 54,352 0,07757

What the table show is that the Age of the Universe and 1/H0 (Hubble Time) are identical. In order to build this table the Friedmann equation is used, with the aid of the excel program Friedmann's equation.xls
To build the first line:

Set parameter Age to 10 and modify the parameter Lambda such that the parameter 1/H0 is equal to the parameter Age

The importance of this exercise is that the value for Omega(M) of 0,26257 is the current accepted value.
That inturn means if you know H0 you can calculate the age of the Universe using the Friedmann equation.
At the same time this means that both the value of Omega(M) and H0 both should be measured without using the Friedmann equation. The way to go is by means of the CMB radiation.

Document Literature (25) at page 13 clearly shows how H0 is calculated:

This measurement of H0 is obtained from the magnitude-redshift relation of 240 low-z Type Ia supernovae at z < 0.1.

That means it uses the friedmann equation!

Literature (19) "Solves" the coincidence problem by introducing a variable Constants. In fact what they do is to change the friedmann equation.

Question 13: Is it possible to calculate the paramaters H0, omega(Lambda), Omega(M) alone using the CMB radiation

First some technical information:

The Cosmological Parameters: H, Omega(Lambda), Omega(M), Omega(K), The Age of the Universe versus the CMBR

Next a more philosophical discussion:

In the book: Handbook of Physics" By Prof Dr. R. Kronig 1958 at page 45 we can read (translated):

The sum of kinetical and potential energy is constant, during the movement of a particle under influence of a conservatif power field

This is the Law of Conservation of Energy . This law is only true under the condition that the power field is conservatif. If this is not the case, than the Law "Conservation of Energy" is not true in this form.
Next we have two choices:

1. Accept that the law is not valid in these cases.
2. By adding different forms of energy we can try to save the law of: Conservation of Energy.

All of this is 100% true.